elliptic

https://www.cnblogs.com/qcblog/p/8998045.html

 

http://www.doc88.com/p-0971398500383.html

 

https://wenku.baidu.com/view/65d4db50be23482fb4da4c13.html

 

 

一、概述

椭圆曲线加密算法依赖于椭圆曲线理论，后者理论涵盖的知识比较深广，而且涉及数论中比较深奥的问题。经过数学家几百年的研究积累，已经有很多重要的成果，一些很棘手的数学难题依赖椭圆曲线理论得以解决（比如费马大定理）。

本文涉及的椭圆曲线知识只是抽取与密码学相关的很小的一个角落，涉及到很浅的理论的知识，同时也是一点比较肤浅的总结和认识，重点是利用椭圆曲线结合数学技巧阐述加密算法的过程和原理。

本文特意构造有比较多的实例方便理解其过程和原理。

二、椭圆曲线

椭圆曲线方程来源于椭圆积分，后者来最初来源于计算椭圆周长的问题，有一段时间的历史了，在欧拉时期就开始研究。椭圆周长没有精确的初等函数的公式表示，只有近似的公式表示，精确的椭圆周长可以用不定积分表示。

现在一般将形如如下形式的积分定义为椭圆积分：

𝑓(𝑥)=∫𝑥𝑐𝑅[𝑡,𝑃(𝑡)‾‾‾‾√]𝑑𝑡

其中𝑅

是其两个参数的有理函数，𝑃是一个无重根的3或4阶多项式，而𝑐是一个常数。椭圆曲线方程与𝑃(𝑡)

表现形式比较相像。

数学上的椭圆曲线一般由如下形式给出：

𝐸:𝑦2=𝑥3+𝑎𝑥2+𝑏𝑥+𝑐

，其中判别式Δ(𝐸)=−4𝑎3𝑐+𝑎2𝑏2−4𝑏3−27𝑐2+18𝑎𝑏𝑐≠0

椭圆曲线都是关于X轴对称的曲线。

典型的椭圆曲线如：𝑦2=𝑥3−4𝑥2+16

，其图像为：

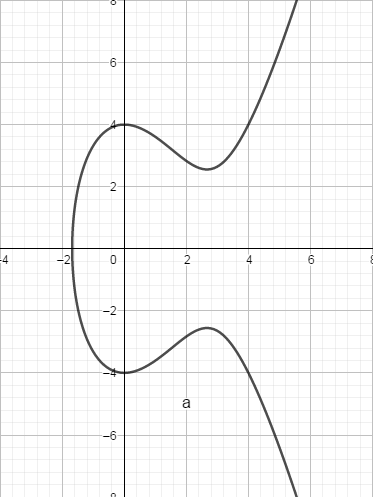
更多的椭圆曲线图像：

 限定Δ

不为零有特殊的意义。如果判别式Δ(𝐸)等于零，由三次方程判别式判定理可知，方程𝑥3+𝑎𝑥2+𝑏𝑥+𝑐=0

存在二重根或者三重根，曲线表现为"自相交"或者有“尖点”。

两个典型的例子是:

𝐶1:𝑦2=𝑥3

𝐶2:𝑦2=𝑥3+𝑥2

𝐶1

有三重根，表现为有"尖点"；𝐶2

有二重根，表现为“自相交”，它们都不是椭圆曲线，其图像分别如下：

                          

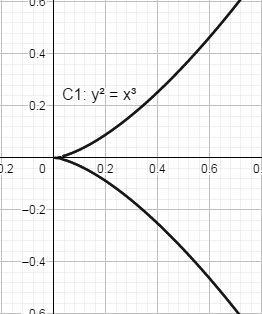
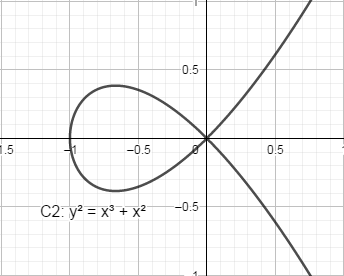
在密码学中用到的椭圆曲线方程一般限定为：

𝐸:𝑦2=𝑥3+𝑎𝑥+𝑏

，其中4𝑎3+27𝑏2≠0

。

也即是这里的二次项系数为0。

三、椭圆曲线算术

椭圆曲线上可以定义一些很有意思的特殊运算规则。一般来说会定义两种运算：加法和数乘运算。加法运算是点与点之间的运算；数乘运算基于加法运算，重复的加法运算就是数乘。

1、实数域的加法运算

1.1、加法运算的几何解释

已知椭圆曲线上两个不同的点𝑃

和𝑄，则这两个点之和𝑅=𝑃+𝑄可以通过如下操作得到：过𝑃、𝑄两点做直线𝐿，与椭圆曲线相交于第三点，该点关于X轴的对称点即是所求的𝑅

点。椭圆曲线的这种加法运算有比较明确的几何含义。如下所示：

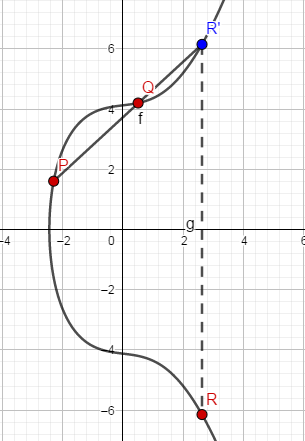
以这种比较奇特的规则来定义加法运算会让人觉得比较怪异，其思想很可能是借鉴于求椭圆曲线有理解的方法（没有去严格考据）。

求椭圆曲线有理解考虑的问题是寻找有理点(𝑥,𝑦)

使其满足椭圆曲线方程。其求解过程是在有限的已知有理点的集合中，选两个点𝑃1,𝑃2，作直线与椭圆曲线相交与第三点个有理点𝑄3。此时如果再利用𝑃1,𝑃2,𝑄3三个点中的任意两点作直线不能在产生新的有理解（因为他们本身是已经在一条直线上，不会产生新的交点），但是考虑𝑄3关于X轴对称的点𝑄′3必定也是有理点，于是可以利用𝑄3′与𝑃1或者𝑄3′与𝑃2

继续做直线与椭圆曲线相交得到新的有理解，对新的交点再取对称点，以此迭代下去。由此利用交点的对称点作直线来生成新的交点，进而可逐步求解满足椭圆曲线的有理解。

椭圆曲线加法运算的规则中“取交点的对称点”正是与上述求解过程及其相似。

对于加法运算也有另外一种描述：若椭圆曲线上三个点在同一直线上，则他们的和为𝑂

，也即是𝑃+𝑄+𝑅′=𝑂，其中的𝑂

是无穷远点或者零点。

更完整的椭圆曲线加法运算规则如下：

1、𝑂+𝑂=𝑂

，对任意的𝑃，有𝑃+𝑂=𝑃；𝑂

看做零点，对加法运算没有实际贡献（类似于四则运算加法运算中的0）。

2、𝑃=(𝑥,𝑦)

的负元是关于X中对称的点−𝑃=(𝑥,−𝑦)（而不是关于原点对称），𝑃+(−𝑃)=𝑂。过𝑃和−𝑃的直线与X轴垂直，实际上可以看做它与椭圆曲线相交于无穷远点（射影平面，也即是在欧式平面上添加了无穷远点和无穷远直线的平面），因此将也将𝑂

视作无穷远点。

3、计算𝑃

和𝑄的和是通过做过𝑃和𝑄两点的直线，与椭圆曲线相交于第三点，再取该点关于X轴的对称点以此作为𝑃,𝑄

之和，正如上面的几何图形展示的那样。

4、计算𝑃

点（𝑃≠𝑂）的两倍时，是做该点的切线，再取交点𝑆关于X轴的对称点−𝑆，也即是2𝑃=𝑃+𝑃=−𝑆

容易验证，对于椭圆曲线上的点和𝑂

点组成的集合，以及集合上定义的二元加法运算，构成一个Abel群。单位元是𝑂点，𝑃(𝑥,𝑦)的逆元是𝑃(𝑥,−𝑦)

，封闭性，结合性以及交换性也是显然满足的。

1.2、加法运算的代数解释

几何解释更直观，代数解释更有利于数值计算。

过曲线上𝑃(𝑥𝑝,𝑦𝑝)

和𝑄(𝑥𝑄,𝑦𝑄)两点（𝑃和𝑄

不互为负元）做直线，求与曲线的第三个交点的问题是很容易用代数的方法来描述的。

也即是求：

{𝑦2=𝑥3+𝑎𝑥+𝑏𝑦−𝑦𝑝=𝑘(𝑥−𝑥𝑝)(1)(2)

其中斜率𝑘=𝑦𝑄−𝑦𝑃𝑥𝑄−𝑥𝑃

。

将（2）代入（1）再利用次数对齐的方式容易求得第三个交点的对称点也即𝑃,𝑄

之和𝑅(𝑥𝑅,𝑦𝑅)

为：

𝑥𝑅=𝑘2−𝑥𝑃−𝑥𝑄

𝑦𝑅=−𝑦𝑃+𝑘(𝑥𝑃−𝑥𝑅)

如果需要计算倍乘，可以让多个点自身重复相加得到。例如𝑃+𝑃=2𝑃=𝑅

，当𝑦𝑃≠0

时，代数描述为：

𝑥𝑅=(3𝑥2𝑃+𝑎2𝑦𝑃)2−2𝑥𝑃

 

𝑦𝑅=(3𝑥2𝑃+𝑎2𝑦𝑃)(𝑥𝑃−𝑥𝑅)−𝑦𝑃

2、模素数P的加法运算

密码学中普遍采用的是有限域上的椭圆曲线，也即是变元和系数均在有限域中取值的椭圆曲线。使用模素数𝑝

的有限域𝑍𝑝，将模运算引入到椭圆曲线算术中，变量和系数从集合0,1,2,...,𝑝−1

中取值而非是在实数上取值。

此时讨论椭圆曲线形式如下：

𝑦2mod𝑝=(𝑥3+𝑎𝑥+𝑏)mod𝑝

其中(4𝑎3+27𝑏2)mod𝑝≠0mod𝑝

，变量和系数均在𝑍𝑝

中取值。

将满足上式的所有非负整数对和𝑂

点记为集合𝐸𝑝(𝑎,𝑏)，这是一个有限的离散点集。由此可知集合中的点分布在(0,0)到(𝑝−1,𝑝−1)的象限中，集合中的点有可能刚好也在椭圆曲线上，更多的可能是在椭圆曲线外。例如点(13,7)是满足𝑦2mod23=(𝑥3+𝑥+1)mod23的点，但是(13,7)

并不在椭圆曲线上。

实际上，集合𝐸𝑝(𝑎,𝑏)

与模𝑝

的加法运算构成循环阿贝尔群，其生成元，阶和生成子群问题在本节后面会讨论。

对于较小的素数𝑝

，完全可以暴力穷举找出集合𝐸𝑝(𝑎,𝑏)中的点。比如参数𝑎=1,𝑏=3,𝑝=23，𝐸23(1,3)

有27个点（包含O点），暴力穷举这些点分别为（第八节给出了一些分析椭圆曲线问题的demo实现）：

(0,7)        (6,15)        (15,9)
(0,16)       (7,10)        (15,14)
(2,6)        (7,13)        (19,2)
(2,17)       (10,1)        (19,21)
(4,5)        (10,22)       (21,4)
(4,18)       (12,8)        (21,19)
(5,8)        (12,15)       (22,1)
(5,15)       (14,1)        (22,22)
(6,8)        (14,22)        O

𝐸𝑝(𝑎,𝑏)

上的加法规则和实数域上的加法基本一致，只是多加了模运算。但是模𝑝

的加法没有显而易见的几何解释，只有代数描述。

求解(𝑥𝑅,𝑦𝑅)

的代数表达式为：

𝑥𝑅=(𝜆2−𝑥𝑃−𝑥𝑄)mod𝑝

𝑦𝑅=(𝜆(𝑥𝑃−𝑥𝑅)−𝑦𝑃)mod𝑝

其中

𝜆=⎧⎩⎨⎪⎪(𝑦𝑄−𝑦𝑃𝑥𝑄−𝑥𝑃)mod𝑝(3𝑥2𝑃+𝑎2𝑦𝑃)mod𝑝(𝑃≠𝑄)(𝑃=𝑄)

例如𝑎=1,𝑏=1,𝑝=23,𝑃(3,10),𝑄(13,16)

，求𝑅=𝑃+𝑄

.

此时𝑃≠𝑄

，计算𝜆=(𝑦𝑄−𝑦𝑃𝑥𝑄−𝑥𝑃)mod𝑝=(16−1013−3)mod23=6×10−1mod23

.

要计算上式首先要计算10−1mod23

.

令𝑥≡10−1(mod23)

，由于10≡10(mod23)，所以10𝑥≡1(mod23)，利用扩展欧几里德算法求得𝑥=7

.

𝜆=6×7mod23=19

所以

𝑥𝑅=(𝜆2−𝑥𝑃−𝑥𝑄)mod𝑝=(192−3−13)mod23=345mod23=0

𝑦𝑅=(𝜆(𝑥𝑃−𝑥𝑅)−𝑦𝑃)mod𝑝=(19×(3−0)−10)mod23=47mod23=1

所以𝑅=(0,1)

.

还可以按照以上规则计算2𝑃,3𝑃

等等倍乘点。

实际上𝐸23(1,1)

中共有28个点（包含无穷远点𝑂），以𝑃(3,10)开始的所有倍乘点：𝑃,2𝑃,3𝑃...27𝑃,28𝑃

可以暴力计算得出:

P=(3,10)
2P=(7,12)
3P=(19,5)
4P=(17,3)
5P=(9,16)
6P=(12,4)
7P=(11,3)
8P=(13,16)
9P=(0,1)
10P=(6,4)
11P=(18,20)
12P=(5,4)
13P=(1,7)
14P=(4,0)
15P=(1,16)
16P=(5,19)
17P=(18,3)
18P=(6,19)
19P=(0,22)
20P=(13,7)
21P=(11,20)
22P=(12,19)
23P=(9,7)
24P=(17,20)
25P=(19,18)
26P=(7,11)
27P=(3,13)
28P=O

容易验证，上述计算过程中𝑄(13,16)

点就是8𝑃，𝑃+𝑄=𝑃+8𝑃=9𝑃=(0,1)

，与上述计算结果是吻合的，读者也可以验证更多的结果。

现在提出一个问题：𝐸𝑝(𝑎,𝑏)

中有多少个点呢？这个问题的准确答案并不好回答，但是有一些粗略的规律。

设𝐸𝑝(𝑎,𝑏)

中点的个数为𝑁𝑝，并且𝑎𝑝=𝑝−𝑁𝑝，实际上𝑁𝑝与𝑝

比较接近。

Hasse定理表明：

∣∣𝑎𝑝∣∣<2𝑝√

这实际上解释了𝑎𝑝

的误差，从而有−2𝑝√<𝑎𝑝=𝑝−𝑁𝑝<2𝑝√

也就是𝑝−2𝑝√<𝑁𝑝<𝑝+2𝑝√

，等价于𝑝+1−2𝑝√⩽𝑁𝑝⩽𝑝+1+2𝑝√

接下来的一个问题是子群、生成元和阶：

不难得知，有限域上的椭圆曲线的点和加法运算构成一个有限交换群𝑆

。

以一个点𝐺

作为生成元，进行重复的加法运算，能够生成一个子群𝑆′。群𝑆′有可能与𝑆相同，更有可能是𝑆

的一个真子群。

比如椭圆曲线为𝑦2=𝑥3+𝑥+1

，𝑝=23

以𝐺=(3,10)

生成的子群刚好等于𝑆，因为28𝐺=𝑂，说明此时𝑆还是一个有限循环群，群中每个元素都能由(3,10)通过重复的加法运算得到，群中元素的个数为28，其阶为28(最小的使得𝑛𝐺=𝑂成立的𝑛)，生成元为(3,10)

。

但是以𝐺=(6,19)

生成的子群是𝑆的真子群，因为14𝐺=𝑂，它也是一个有限循环群，因为群中每个元素都能由(6,19)通过重复的加法运算得到，该子群的元素个数为14，阶为14（最小的使得𝑛𝐺=𝑂的成立𝑛），生成元为(6,19)

。

拉格朗日定理还告诉我们，生成的子群𝑆′

的阶与原来的群𝑆的阶存在约数关系，也就是说子群𝑆′的阶只能是1,2,4,7,14,28。群𝑆的阶与子群𝑆′的阶的比值一般称为协因子(cofactor)：ℎ=|𝑆|∣∣𝑆′∣∣。一般会取ℎ=1

，以保证生成子群的阶比较大。

以𝐺=(6,19)

生成子群过程（为方便计算，取𝑂=(−1,−1)

）：

1P=(6,19)        15P=(6,19)
2P=(13,16)       16P=(13,16)
3P=(7,11)        17P=(7,11)
4P=(5,19)        18P=(5,19)
5P=(12,4)        19P=(12,4)
6P=(17,20)       20P=(17,20)
7P=(4,0)         21P=(4,0)
8P=(17,3)        22P=(17,3)
9P=(12,19)       23P=(12,19)
10P=(5,4)        24P=(5,4)
11P=(7,12)       25P=(7,12)
12P=(13,7)       26P=(13,7)
13P=(6,4)        27P=(6,4)
14P=(-1,-1)      28P=(-1,-1)

 在后面的ECC加密算法过程中会有一个给定的基点𝐺

（也就是生成元）生成一个子群，然后秘钥空间在此子群取得，一般会要求保证子群的阶会尽量大，基点及其子群的阶𝑛

都是公开的信息。

四、椭圆曲线密码学中的离散对数问题

构造一个数学难题来保证加密的安全性是现代密码学中加密算法的主要思想。类似RSA算法中大数的质因子分解难题一样，椭圆曲线也有类似的数学难题。

考虑𝑄=𝑘𝑃

，其中𝑄,𝑃∈𝐸𝑝(𝑎,𝑏),𝑘<𝑝

。

对于给定的𝑘,𝑝

计算𝑄是很容易的；反过来给定𝑄,𝑃，计算𝑘

是相当困难的，这就是椭圆曲线的离散对数问题（这里之所以称之为离散对数问题大概是为了与其他加密算法的说法保持一致，便于理解）。

正因为如此，可以将𝑄

作为公钥，公开出去；𝑘

作为私钥，秘密保管，通过公钥来破解私钥十分困难。

目前由椭圆曲线公钥求解私钥的最有效算法复杂度为𝑂(𝑝√)

，其中𝑝是阶数𝑛

的最大素因子。

五、椭圆曲线实现秘钥协商（ECDHE）

1、原理和流程

 利用模𝑝

有限域上椭圆曲线算术规则可以用来实现秘钥协商，其流程如下：

（1）Alice和Bob会共享一些椭圆曲线的参数信息：(𝑝,𝑎,𝑏,𝐺,𝑛,ℎ)

，其中𝑎,𝑏确定了椭圆曲线方程，𝑝确定了模𝑝的有限域，G是中的生成元，用于生成子群，要求𝐺的阶𝑛应该尽量大，𝐺的阶是使得𝑛𝐺=𝑂成立的最小的整数，也即是(𝑛−1)𝐺所代表的点与𝐺点的横坐标刚好相同，协因子ℎ

一般等于1。

（2）Alice选择小于𝑛

整数𝑛𝐴，然后计算𝑃𝐴=𝑛𝐴×𝐺，将𝑃𝐴

发送给Bob。

（3）同理，Bob也选择小于𝑛

整数𝑛𝐵，然后计算𝑃𝐵=𝑛𝐵×𝐺，将𝑃𝐵

发送给Alice。

（4）Alice通过如下计算得出协商的秘钥：𝐾𝐴=𝑛𝐴×𝑃𝐵

；Bob通过如下计算得出协商的秘钥：𝐾𝐵=𝑛𝐵×𝑃𝐵，容易证明，𝐾𝐴=𝐾𝐵

。

因为𝐾𝐴=𝑛𝐴×𝑃𝐵=𝑛𝐴×(𝑛𝐵×𝐺)=𝑛𝐵×(𝑛𝐴×𝐺)=𝐾𝐵

。

由此Alice和Bob计算得到相同的秘钥，达到秘钥协商的目的。

2、实例

例如，参数𝑎=0,𝑏=−4

，椭圆曲线方程为𝑦2=𝑥3−4，𝑝=211,𝐺=(2,2)，因为240𝐺=(2,209)所以𝑛=241

。

Alice选择𝑛𝐴=151

，𝑃𝐴=151𝐺=(62,59)

；

Bob选择𝑛𝐵=171

，𝑃𝐵=171𝐺=(209,153)

；

他们协商的秘钥𝐾=151𝑃𝐵=171𝑃𝐴=151(209,153)=171(62,59)=(95,194)=(151∗171%𝑛)𝐺=34𝐺

。

六、椭圆曲线实现加解密

1、原理和流程

利用椭圆曲线来进行加密和解密也是与RSA一定程度的类似，每一个用户都有属于自己的公钥和私钥。私钥就是用户选定的数字𝑛

，私钥自己保存；公钥就是由𝑃=𝑛𝐺

，计算出来的点，公钥公开。

假设Alice与Bob进行加密通信，其加密的流程如下：

（1）Alice首先将明文消息转换（编码）为𝐸𝑝(𝑎,𝑏)

中的𝑃𝑚(𝑥,𝑦)，然后随机选定一个正整数𝑘，并且利用Bob的公钥𝑃𝐵

通过如下计算出密文：

𝐶𝑚={𝑘𝐺,𝑃𝑚+𝑘𝑃𝐵}

因此，密文实际上是有两个点组成。

（2）Bob收到密文𝐶𝑚

，利用自己的私钥𝑛𝐵

进行如下计算，可以解密得到明文：

𝑃𝑚+𝑘𝑃𝐵−𝑛𝐵(𝑘𝐺)=𝑃𝑚+𝑘(𝑛𝐵𝐺)−𝑛𝐵(𝑘𝐺)=𝑃𝑚

也就是用第二个点𝑃𝑚+𝑘𝑃𝐵

减去第一个点𝑘𝐺与自己的私钥𝑛

之积。

2、实例

 考虑参数𝑎=0,𝑏=−4,𝑝=199,𝐺=(2,2)

，椭圆曲线方程为𝑦2=𝑥3−4

，

Bob选定的私钥为𝑛𝐵=119

，其公钥𝑃𝐵=119𝐺=(183,173)

。

Alice希望将消息𝑃𝑚=(76,66)

加密后发送给Bob，于是Alice随机选定正整数𝑘=133

，并通过Bob的公钥加密得到密文：

𝐶𝑚={133(2,2),(76,66)+133(183,173)}={(40,147),(180,163)}

Bob收到密文消息利用自己的私钥𝑛𝐵=119

进行解密：

𝑃𝑚+𝑘𝑃𝐵−𝑛𝐵(𝑘𝐺)=(180,163)−119(40,147)=(180,163)−(98,52)=(76,66)=𝑃𝑚

.

由此，Bob顺利解密得到明文消息，Alice与Bob之间完成加密通信。

七、杂项

公钥加密算法中除了ECC，还有另外一个广泛使用的加密算法--RSA公钥加密算法。

ECC与RSA相比，主要的优点是在相同的安全级别下ECC使用的秘钥长度要短很多，由此带来处理速度、带宽和存储空间上的额外优势。下表展示了不同加密算法秘钥的位数对比情况：

比特币中使用椭圆曲线密码算法，以保证比特币网络中信息安全性和签名认证问题。每个用户都有属于自己的公钥和私钥。利用私钥可以对交易信息进行签名（ECDSA），其他人可以利用其公钥进行认证，公钥也用来构造钱包地址。所使用的椭圆曲线是采用了Certicom推荐的椭圆曲线secp256k1 ，其参数由六元组构成：𝐷=(𝑝,𝑎,𝑏,𝐺,𝑛,ℎ)

，其中𝑝是很大的质数，ℎ就是协因子，表征由生成元𝐺

生成子群的阶与母群的阶的关系，前文有解释；参数信息都是公开的，有兴趣可以到网上查到。

八、数值计算Demo实现

以下实现一些比较常用的方法，主要涉及暴力穷举𝐸𝑝(𝑎,𝑏)

中的点（无穷远点O=(-1,-1)），求有限交换群的阶，椭圆曲线加法运算和乘法运算，以及相关的求模反元素和扩展欧几里德算法等。主要在学习椭圆曲线加密过程中，方便快速的构造用例和实验、验证。主要实现核心的计算原理，细节部分的处理难免有疏漏。

/**
 * Date:2018.05.16
 * Author:Qcer
 * Function:ECC
 * */
package com.demo;
import java.util.ArrayList;
public class ECCImpl {
    private long a = 0;
    private long b = 0;
    private long p = 0;
    private ECCImpl() {}
    public ECCImpl(long a, long b, long p) {// 参数初始化，椭圆曲线方程:y^2=x^3+ax+b的形式，
        this.a = a;
        this.b = b;
        this.p = p;
    }
    // 暴力搜索(0,0)到(p-1,p-1)象限且满足模p方程的所有点
    public ArrayList search() {
        ArrayList<Long[]> list =new ArrayList<>();
        long left,right;
        for (long x = 0; x < p; x++) {//i=x   from 0 to p-1
            for (long y = 0; y < p; y++) {//j=y form 0 to p-1
                left = y * y % p;
                right = (x * x * x + a * x + b) % p; 
                if (left == right) {
                    list.add(new Long[] {x,y});
                    System.out.println("("+x+","+y+")");
                }
            }
        }
        return list;
    }
    //获取椭圆曲线上有限交换群的阶，包含无穷云巅O
    public long getOrder() {
        return search().size()+1;
    }
    //自定义求模运算，主要考虑a小于0的情况
    public long mod(long a, long p) {
        long r = Math.abs(a) % p;
        return a >= 0 ? r : p - r;
    }
    //椭圆曲线上的加法运算,R=P+Q
    public long[] add(long x1, long y1, long x2, long y2) {
        if (x1 == -1) {// O+P=P
            return new long[]{x2,y2};
        }
        if (x2 == -1) {// P+O=P
            return new long[]{x1,y1};
        }
        long[] point = new long[2];
        long ratio = 0;//系数    0<=ratio<=p-1
        if (x1 == x2) {
            if (y1 == y2) {// P==Q
                ratio = mod((3  *x1 * x1 + a) * (getMMI(2 * y1,p)),p);
            }else { // P+P=O
                return new long[] {-1,-1};
            }            
        }else {// P!=Q
//            long flag = (y2-y1)*(x2-x1)>0?1:-1;//锚定正负号
            long mask = 1<<63;
            long flag = (((y2 - y1) & mask) ^ ((x2 - x1) & mask)) == 0 ? 1 : -1;
            ratio =  mod(flag * Math.abs(y2 - y1) * (getMMI(Math.abs(x2 - x1),p)),p);
        }
        point[0] = mod(ratio * ratio - x1 - x2, p);
        point[1] = mod(ratio * (x1 - point[0]) - y1,p);
//        System.out.println("("+point[0]+","+point[1]+")");
        return point;
    }
    //椭圆曲线上的乘法运算,乘法运算定义为重复的加法运算:kP=P+P+P+...+P
    public long[] multiply(int x, int y, int times) {
        long[] point = {x,y};
        for (long i = 2; i <= times; i++) {
            point = add(point[0],point[1],x,y);
            System.out.println(i+"P="+"("+point[0]+","+point[1]+")");
            if (point[0] == -1) {
                return point;
            }
        }
        System.out.println(times+"P="+"("+point[0]+","+point[1]+")");
        return point;
    }
    //利用扩展欧几里算法得求模范元素,ax=1(mod b) => ax+b(-y)=1=gdc(a,b)
    public long getMMI(long a, long b) {//modular multiplicative inverse
        long mmi = gcdExt(a,b)[1];
        while (mmi < 0) {
            mmi += b;
        }
        return mmi;
    }
    //扩展欧几里得算法:ax+by=g=gcd(a,b)  =>  tuple[1]x+tuple[2]y=gcd(a,b)
    public long[] gcdExt(long a, long b) {
        long ans;
        long[] tuple = new long[3];
        if (b == 0) {
            tuple[0] = a;
            tuple[1] = 1;
            tuple[2] = 0;
            return tuple;
        }
        long[] temp = gcdExt(b,a%b);
        ans = temp[0];
        tuple[0] = ans;
        tuple[1] = temp[2];
        tuple[2] = temp[1] - (a / b) * temp[2];
        return tuple;
    }
    public static void main(String[] args) {
        // TODO Auto-generated method stub
//        ECCImpl ecc = new ECCImpl(0, -4, 199);//0, -4, 211
//        ecc.search();
//        ecc.add(3,10,13,16);
        ECCImpl ecc = new ECCImpl(1, 1, 23);
        System.out.println(ecc.getOrder());
//        ecc.search();
//        ECCImpl ecc = new ECCImpl(4, 20, 29);
//        ecc.search();
        
//        ecc.multiply(12,19, 28);
    }
}

九、References

1、密码编码学与网络安全原理与实践

2、http://andrea.corbellini.name/

3、数论概述.第四十三章-第四十八章

4、https://mp.weixin.qq.com/s/jOcVk7olBDgBgoy56m5cxQ

5、https://blog.csdn.net/mrpre/article/details/72850598