FIR滤波器工作原理(算法)以及verilog算法实现(包含与IIR的一些对比)
滤波器在2017年IC前端的笔试中,出现频率十分的高。不论今后是否会涉及,还是要记住一些会比较好。接下来就将从这四个方面来讲解,FIR数字滤波器的工作原理(算法)与verilog实现。
·什么是FIR数字滤波器
·FIR数字滤波器与IIR数字滤波器的对比
·从sobel算法、高斯滤波算法着手,讲解FIR滤波器算法
·FIR数字滤波器的几种verilog代码实现
一、什么是FIR数字滤波器
FIR滤波器的全称是Finite Impulse Respond Filter。中文全称是有限脉冲响应滤波器,它也叫做非递归型滤波器。
它的作用和所有的滤波器一样,通过算法来使某刻的值处在一个更为准确的值,这句话看着很绕,但是在后面的三种算法的介绍中,应该可以理解我在这里说的这句话的含义。(它比‘通过算法来去除杂波’这句话,更清楚明白)。
实现数字滤波,就必须要有数字信号,所以这里要通过A/D转换,来使得模拟信号变为数值,才好带入算法中计算,然后用D/A转换,输出模拟信号。
二、FIR数字滤波器与IIR数字滤波器的对比
这里说了与IIR数字滤波器的对比,那什么是IIR数字滤波器呢?
IIR数字滤波器全称是Infinite Impulse Respond Filter。中文全称是无限脉冲响应滤波器,它也叫做递归型滤波器。
二者特点比较:
FIR滤波器特点:
- 没有反馈回路,稳定性强。即FIR滤波器只需要有当前数据,和历史输入数据,不需要历史滤波输出数据的参与(这是它与IIR最大的区别了,后面许多差别也就是因为这个而来的)。因为滤波的输出本来就是一个舍入值,若带入下一次的计算中,就会在这个舍入值(非精准值)基础上再一次的舍入,进行N次,会产生微小的寄生振荡。
- 算法计算完成后与原先数据有线性的相位差,更容易将计算后的信号相位还原成原相位(通过左右平移的方式直接修正)。
- 相对于IIR数字滤波器,在相同性能指标下,阶次(就是后面所说的N次选点)较高,对CPU的消耗更大。
IIR滤波器特点:
- 系统函数可以写成封闭函数的形式,具有反馈回路。这个反馈回路的加入,使得在相同CPU消耗下,IIR的精确度不如FIR,但在较小的相同阶次下,也是它使得IIR的效果要比FIR更好,成也反馈败也反馈。
- 算法计算完成后与原先数据的相位差不是线性的,这就使得在修正相位差的时候会很麻烦。
- FIR滤波器特点第一条就说了,IIR可能会产生寄生振荡。
下面的两幅图是我自己画的,一个是FIR滤波后(并进行D/A转换后)与IIR滤波后的相位差对比图,一个是基于FPGA的功能对比图。
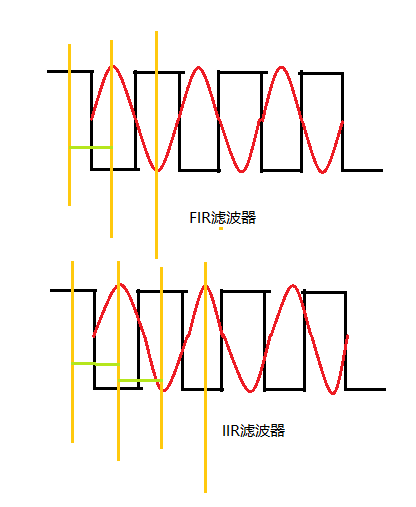
图1
从图1中可以看出来,IIR滤波后,相位与原先是非线性的。而FIR是线性的。
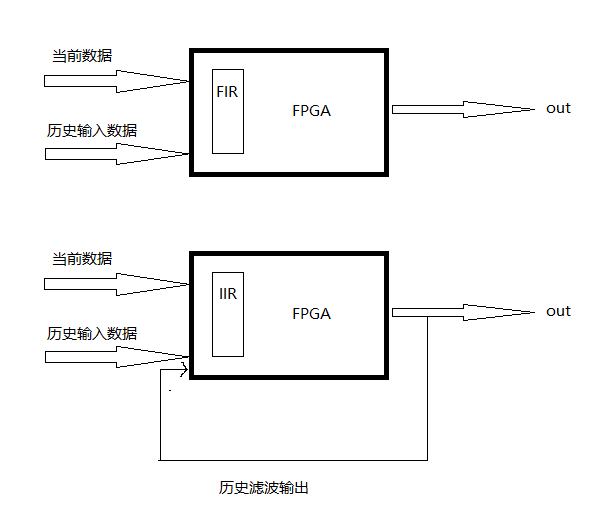
图2
从图2中可以看到IIR明显存在一个反馈过程。
对于不同滤波需求该怎么选择呢?
应用选择:
- 对于相位要求不敏感的场合用IIR,它对CPU需求较低,充分发挥经济高效的特点。
- 对于做图像信号处理、数据传输等以波形携带信息的场合,要使用FIR,比起CPU资源的消耗,我们更关心的是结果的准确。(在许许多多的设计中都是同样的道理,想得到什么就得失去什么,不可能在同等工艺基础上,又快又省功耗面积又小的。)
三、从sobel算法、高斯滤波算法着手,讲解FIR滤波器算法
下面从sobel算法开始,慢慢道来。
sobel算法
Sobel算法是用在检测像素边沿点的一种算法。
边沿点。一幅美丽的照片,不可能是单纯的一种颜色,那在各个色彩的交阶位置就是边沿点。
通过带入计算sobel卷积因子,计算出I GX I、I GY I,两者相加得到的G的值与规定标准值(一个确定的边沿点带入卷积因子计算后得到的一个标准值) 进行比较。若大于等于标准值则认为是一个边沿点。
sobel卷积因子
Gx: -1 0 +1 Gy: +1 +2 +1
-2 0 +2 0 0 0
-1 0 +1 -1 -2 -1
卷积因子的使用:
比如说下面是一个巨大的像素屏,选择一点为检测对象(红色标记),那这一点就对应了卷积因子最中间的点,其它八个点对应像素上的八个点(蓝色标记)。
口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口
将各个点的值与对应相同位置的卷积因子相乘,之后将得到的9个值相加,并求绝对值,得到的就是Gx与Gy的绝对值,两者相加为G,再将G于标准值进行比较,得到改点是否为边沿点。
为什么这么做就可以检测出边沿点了呢?
从卷积因子可以看出,两次计算之后,其实是拿待检测点与相邻、相斜对角的值做放大,上下左右直接与待检测点相连的值放大了两倍,就像一个显微镜,把中间点和四周点点色彩的区别放大了,这就是检测的原理。
高斯滤波算法
高斯滤波算法可以用来优化图像,举个最直白的道理,你拍了一张自拍照,但是上面的小豆豆很是讨厌,而使用高斯滤波算法可以使得这些讨厌的小豆豆全部变淡,或者消失。
是不是引发了爱美的你的强烈的兴趣?接下来看一下卷积因子。
1 2 1
2 4 2
1 2 1
口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口口
脑补上面是一幅图画,每幅图也都是由像素点组成。我们假设红色的点是痘痘,那我们要经过高斯滤波算法,将它变为和周边皮肤(蓝色标记)颜色相同。
设九宫格内数值依次是x0,x1,x2,x3,x4,x5,x6,x7,x8。其中x4是我们要优化的点。设值为y:
Y = (x0*1+x1*2+x2*1+x3*2+x4*4+x5*2+x6*1+x7*2+x8*1)/16
这个计算出来的值就是优化值。下面看看原理:
细心的朋友会发现与sobel算法不同之处在于,最后还要除以16。为什么呢?
因为所有的因子相加是16,如果不除以16那么就会将优化值放大16被,那就是说这个痘痘反而变得与周围皮肤更加的凸显了,这显然不是我们想要的。
总结:
上面两个算法的目的是什么?引用上面两个算法,是为了让大家更好的了解这种卷积式的算法,以及它的原理,下面的FIR滤波器算法和上面两者有很多相似之处。
FIR滤波器算法
终于到了正题,能坚持看到这里的朋友,下面对于FIR的分析一定不会让你失望。
直接掏出算法公式:
Y(N) = h(0)*x(N)+h(1)*x(N-1)+``````+h(k-1)*x(N-(k-1))
Y(N)表示的是第N个取样点纵坐标的优化值
X(N)表示的是第N个取样点横坐标的值(取样值)
h()表示系数,后面会有系数的求取方法
这里的h系数就类似于前面说的卷积因子,只不过这卷积因子的数量并不确定的,并且并不是每个取样点都会加入计算,它与系数的个数有关。所以可以这么说,FIR滤波器取的系数越多,计算的越精确(当然N要大于k),但是消耗的cpu资源也会越多。毕竟从上式可以看出这是好多加法器乘法器组成的。
滤波原理同类似于上述两种算法,(神似而已)最后的系数相加肯定必须还是1。
很重要的一点h的取值是可以用matlab软件计算出来的,具体方法,请自行搜索FIR滤波器算法系数的计算,因为只是一些软件的使用,这里不在讲述。
四、FIR数字滤波器的几种verilog代码实现
我们假设N = 8 k = 7
实现算法一:
always@ (posedge clk or negedge rst_n) begin
if (rst_n == 1’b0) begin
end
else if(vld) begin
y <= x0*h7+x1*h6+x2*h5+`````+x7*h0;
end
end
涉及时序用非阻塞,具体原因可以看我之前写的verilog编写规范里面的关于阻塞和非阻塞区别的解释。
这个算法好吗?
它对于人类来说是友好的,一目了然。但是对于整个FIR数字滤波器的硬件设计却是非常不友好的。上面用了一长串的赋值语句来计算y的值。但从硬件上体现,这就是加法器和乘法器啊,这么多的加法器乘法器,那得多大的延迟啊?所以可以看一下算法二:
实现算法二: 流水线,并行乘法
always@ (posedge clk or negedge rst_n) begin
if (rst_n == 1’b0) begin
end
else if(vld) begin vld是指示信号,说明数据进来了
m0 <= x0*h7;
m1 <=x1*h6;
`
`
`
m7 <= x7*h0;
end
end
always@ (posedge clk or negedge rst_n) begin
if (rst_n == 1’b0) begin
end
else if(vld_ff0) begin
n0 <= m0 + m1;
n1 <= m2 + m3;
`
`
`
n3 <= m6 + m7;
end
end
always@ (posedge clk or negedge rst_n) begin
if (rst_n == 1’b0) begin
end
else if(vld_ff1) begin
z0 <= n0 + n1;
z1 <= n2 +n3;
end
end
always@ (posedge clk or negedge rst_n) begin
if (rst_n == 1’b0) begin
end
else if(vld_ff2) begin
Y <= z0 + z1;
end
end
always@ (posedge clk or negedge rst_n) begin
if (rst_n == 1’b0) begin
end
else if(vld_y) begin
vld_ff0 <= vld;
vld_ff1 <= vld_ff0;
vld_ff2 <= vld_ff1;
vld_y <= vld_ff2;
end
end
虽然采用了流水线的设计,使得各个乘法器、加法器并行计算,大大节省了时间,但是乘法器加法器的个数还是比较多的。能不能就用一个乘法器一个加法器?
实现方法三:
加入一个计数器
always@ (posedge clk or negedge rst_n) begin
if (!rst_n) begin
cnt <= 0;
end
else if(add_cnt) begin
if(end_cnt) begin
cnt <= 0;
end
else begin
cnt <= cnt+1;
end
end
end
assign add_cnt = flag_add;
assign end_cnt = add_cnt && cnt == 8-1;
always@ (posedge clk or negedge rst_n) begin
if (rst_n == 1’b0) begin
end
else if(add_cnt && cnt == 1-1) begin
A <=x0;
B<= h7;
end
`
`
`
else if(add_cnt && cnt == 8-1) begin
a <=x7;
b<= h0;
end
end
always@ (posedge clk or negedge rst_n) begin
if (rst_n == 1’b0) begin
end
else begin
mul <= a + b;
end
end
always@ (posedge clk or negedge rst_n) begin
if (rst_n == 1’b0) begin
y<= 0;
end
else if() begin
y <= y + mul;
end
end
这个方法,只用了一个加法器和一个乘法器,非常省面积,但是它与二相比,不是并行乘和加,所以速度比不上方法二。
在具体设计中会根据具体的情况来选择三种不同的描述方式。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号