ABC 129 - 142 不完全题解
题号带星号(*)的题暂时还不会
ABC129
前三题略
D.lamp
虽然数据范围不大，但也没法暴力 check ，可以考虑分别维护每行（每列）障碍物的纵（横）坐标，可以考虑到插入 std::vector 中，然后对于每一个点查找横竖方向上的前驱后继，再减去 \(3\) 即可。为了方便维护和简化讨论，对于每列可以将 \(0\) 和 \(h+1\) 也插入进 std::vector ，对于行同理
E.Sum Equals Xor
由于满足 \(a+b=a\bigoplus b\) ，且异或本质为二进制不进位加法。因此可得出 \(a\) 和 \(b\) 不能在相同位上同为 \(1\)
可通过数位dp解决该问题，但需保证 \(a\bigoplus b\leq L\) 恒成立
也可通过线性dp解决，定义 \(f[i][0]\) 为前 \(i\) 位与 \(L\) 相同的方案数，\(f[i][1]\) 为前 \(i\) 位小于 \(L\) 的方案数
可得转移方程
F.Takahashi's Basics in Education and Learning(*)
矩阵快速幂，待补
ABC130
前三题略
D.Enough Array
套路题，由于 \(a_i\) 为整数，保证了前缀和的单调性，做出前缀和后对于每一个位置二分即可
E.Common Subsequence
比较有意思的dp，设计状态 \(f[i][j]\) 为 \(a\) 序列前 \(i\) 项与 \(b\) 序列前 \(j\) 项相同子序列的个数
可得转移方程： \(f[i][j]=f[i][j-1]+f[i-1][j]-f[i-1][j-1]\)
该部分有容斥的知识，即 \(|A\bigcup B|=|A|+|B|-|A\bigcap B|\)
需要注意的时，当 \(a[i]=b[j]\) 时，转移方程为 \(f[i][j]=f[i][j-1]+f[i-1][j]\)
最终可得
F.Minimum Bounding Box
算法1：可以大力分类讨论，因为答案只会受到边界点的印象，因此同方向运动只考虑坐标更大（小）的点，但较为复杂
算法2：裸的三分，证明不会，代码实现简单
ABC131
前三题略
D.Megalomania
贪心，按照结束时间排序，然后模拟即可
E.Friendships
考虑点对最多的情况，显然为菊花图
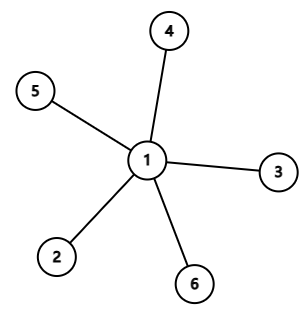
此时点对数量为 \(\sum_{i=2}^{n}n-i=\frac{(n-1)(n-2)}{2}\) ，所以当点数大于该数的时候无法构造
又可以发现，对于初始图中的叶子节点我们每两两连接一条边，点对数量就会减一，因此得到构造方案
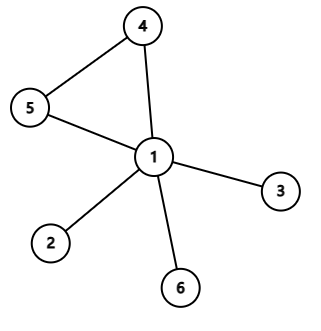
F.Must Be Rectangular!
只有当矩阵的三个顶点确定下来，才能构造出一个矩形
因此可以假设两个横坐标或纵坐标相同的点之间连有一条边
构造一个矩形的过程可以被抽象，假设有横坐标 \(x_1\) 联通了纵坐标 \(y_1\) ，同时 \(y_1\) 还连接了 \(x_2\) ，考虑 \(x_2\) 所连接的纵坐标中是否有和 \(x_1\) 也相连的，如果满足则可以构造为一个矩形
重复该过程直到没有新的矩形出现，该过程等价于构造完全二分图，可用并查集实现，最后用总边数减去 \(n\) 即为答案
ABC132
前三题略
D.Blue and Red Balls
很典的一个组合数问题，首先考虑到将 \(k\) 个蓝色分成 \(i\) 段的方案数可以用隔板法，为 \({i-1}\choose{k}\)
得到 \(i\) 段以后，我们还剩下 \(n-k+1\) 个由红色所组成的空，因此可以再次考虑隔板法，可得最终答案为 \({i-1}\choose{k}\) \(i\choose{n-k+1}\)
E.Hopscotch Addict
考虑设计 \(dp[u][x]\) 表示从起点到 \(u\) 在模 \(3\) 意义下为 \(x\) 时所经过的最少边数，最终的答案为 \(\frac{dp[t][0]}{3}\)
直接用 bfs 转移即可
F.Small Products
设计 \(dp[i][j]\) 为第 \(i\) 位数字为 \(j\) 的方案数，因此可得转移式：
\(dp[i][j]=\sum_{x=1}^{\lfloor\frac{n}{j}\rfloor}dp[i-1][x]\)
显然数组的第二维可能会到 \(10^9\) ，空间复杂度无法接受
考虑优化，利用数论分块，可以将小于等于 \(\sqrt{n}\) 的数字单独分块，剩下的数字与前面 \(\sqrt n\) 块一一匹配，因此转移方程为：
\(dp[i][j] = dp[i][j - 1] + (dp[i - 1][mp[n/blo[j].max]] * blo[j].num\)
其中 \(mp[i]\) 代表第 \(i\) 在第几块内，\(blo[i].max\) 和 \(blo[i].num\) 分别代表第 \(i\) 块中最大的数字和块内有多少数
ABC133
前三题略
D.Rain Flows into Dams
假设 \(a[i]\) 为第 \(i\) 个水坝的水量， \(b[i]\) 为第 \(i\) 座山的水量
递推后可得到
\(b[1]=a[1]-a[2]+a[3]...-a[n-1]+a[n]\)
\(b[i]=(a[i]/2-b[i-1]/2)\times2\)
E. Virus Tree 2
假设节点 \(1\) 为树根，显然该点涂色没有任何限制，因此有 \(k\) 种上色方案
再考虑 \(1\) 的儿子，显然这些节点不能与 \(1\) 颜色相同，因此总共有 \(k-1\) 种颜色可以选择，方案数为 \(A_{sz[1]}^{k-1}\) ，之所以排列而不是选择是因为节点有编号
考虑节点 \(x\) 的儿子，其颜色不能与 \(x\) 节点以及 \(x\) 节点的父亲节点相同，因此只有 \(k-2\) 种颜色可以选择，贡献为 \(A_{sz[x]}^{k-2}\)
可得答案为 \(k\times A_{sz[1]}^{k-1}\prod_{i=2}^{n}A_{sz[i]}^{k-2}\)
F.Colorful Tree
考虑用主席树+LCA解决
对于每一个节点建主席树维护该节点到树根的路径中，相同颜色的边的数量以及该颜色的长度总和
两点之间的路径长度可以描述为 \(dis_i+dis_j-2\times dis_{LCA(i,j)}\) ，再减去原有的权值和，加上 \(y\) 乘边的数量
同样也可以用树剖+主席树维护，但码量较大
树上莫队也能解决 (但我不会
ABC134
前三题略
D.Preparing Boxes
倒序暴力模拟操作即可
E.Sequence Decomposing
可以利用 \(Dilworth\) 定理的结论，最长上升子序列的个数为最长不上升子序列的长度
也可以用 std::multiset 暴力维护每一条链的结尾数值是多少，将新加入的数字插入到可选的所有链中结尾元素最大的链尾
F.Permutation Oddness(*)
很深刻的数数题，待补
ABC135
前三题略
D.Digits Parade
考虑 dp ，设计状态 \(dp[i][j]\) 为前 \(i\) 个数所能组成的所有数字中模 \(13\) 为 \(j\) 的个数
转移方程可得
\(dp[i][(k * 10 + j) \bmod13] = dp[i - 1][k]\)
其中 \(k\) 为枚举余数为 \(0\) 到 \(12\) 的情况，\(j\) 为该位的值，当该位为 \(?\) 时， \(j\) 为 \(0\) 到 \(9\) 所有数字
E.Golf
很有水平的一个构造，自己没做出来，看的题解
首先为了简化条件，使得 \(0\leq X\leq Y\) ，可以通过取绝对值和加 \(K\) 等操作实现
如果 \(K\) 为偶数且 \(X+Y\) 为奇数，答案显然是不能走到的，因为初始点的坐标为 \((0,0)\) ，满足坐标和为偶数，因此接下来的每一步移动都是坐标和为偶数的
对于可以走到的情况，可以通过官方题解给出的方法构造：
F.Strings of Eternity
首先可以将 \(s\) 串倍增至 \(t\) 串的两倍以上然后用 \(kmp\) 暴力匹配，记录一下最多的连续匹配次数，如果答案满足 \(res\geq \frac{|s|}{|t|}\) ，说明后续可以无限匹配，答案为 \(-1\)
题解还提到了一种数最长路个数的做法，看上去很厉害，但是目前没懂😀
ABC136
前三题略
D.Gathering Children
由于运动范围一定保证在这 \(n\) 个位置中，因此运动到一定时间后一定会左右横跳，由于 \(10^{100}\) 是偶数，所以只需要判断开始横跳后偶数时刻各个小孩在哪即可
E.Max GCD
注意到操作不会影响到 \(\sum{a_i}\) ，因此最终答案一定是 \(\sum{a_i}\) 的因数，因此可以只 check \(\sqrt(\sum a_i)\) 个数字
check \(x\) 是否合法时可以将 \(a_i:=a_i\bmod x\) 后排序，用双指针模拟操作，判断操作次数是否小于等于 \(k\)
F.Enclosed Points
可以转化问题，将问题转化为每个点会被多少个子集包含
考虑以每个点作为原点建立平面直角坐标系，只有一、三象限或二、四象限同时有点的时候才会将该点包含，利用容斥减去一三和二四象限都有点的情况即为答案
求各象限点的数量为二维数点问题，利用树状数组即可解决
ABC137
前三题略
D.Summer Vacation
贪心，每天都选取在第 \(m\) 天之前能拿到报酬的最高工资的工作，可以用优先队列维护
E.Coins Respawn
可以将每条边的边权减去 \(P\) ，那么答案将会被转化为寻找 \(1 \rightarrow n\) 的最长路，可以将边权再取反转化为最短路，当图中存在负环时，答案为 \(-1\) ，可以用 \(spfa\) 解决
F.Polynomial Construction（*）
下次一定
ABC138
前三题略
D.Ki
树上差分维护即可
E.Strings of Impurity
建一个子序列自动机并维护 \(s\) 中每个字母第一次出现的位置即可，当 $ch \in T \and ch\notin S $ 时无解
F.Coincidence
数位dp，打表发现对于满足要求的数对 \((x,y)\) ，有两数最高位 \(1\) 相同且除最高位外 \(x\) 为 \(1\) 的数位， \(y\) 为 \(0\) ，\(x\) 为 \(0\) 的数位，\(y\) 也为 \(0\) ，直接进行dp即可
ABC139
前三题略
D.ModSum
显然构造为 \(2,3...n,1\) 时为最优，答案为等差数列求和
E.League
模拟，枚举天数，记录每个人进行到第几场比赛，贪心匹配即可
F.Engines
显然夹角越小的合并越优秀，在极角排序后夹角小的向量会在一个连续的区间里，枚举区间即可
ABC140
前三题略
D.Face Produces Unhappiness
贪心，设首字母为 \('R'\) ，那么则对 \(\min(x,k)\) （ \(x\) 为连续 \('L'\) 段的数量）连续 \('L'\) 段进行操作，操作结束后求值即可
E.Second Sum
对于每个位置维护四个值，左边第一第二个大于该数的位置以及右边第一第二个大于该数的位置即可，可以用 std::set 实现
F.Slime
贪心，在已有的史莱姆中从大到小遍历，每个史莱姆会生出尚未出现的比自己小的史莱姆中最大的史莱姆，可以用 std::multiset 实现
ABC141
前三题略
D.Powerful Discount Tickets
贪心，每次取最大的用打折券即可
E.Who Says a Pun?
dp， 设状态 \(dp_{i,j}\) 为第一个串起始位置为 \(i\) ，第二个串起始位置为 \(j\) 的最大匹配长度
SA 求出 LCP 后暴力求出 \(\max(|i - j|,LCP(i,j))\) 也可
F.Xor Sum 3
线性基，按位考虑，出现次数为奇数的位显然可以直接贡献答案，不必继续考虑
出现次数为偶数的要尽量合理划分使得结果最大，可以用线性基实现。在插入线性基前要记得将出现次数为奇数的位全部置为 \(0\)
ABC142
前三题略
D.Disjoint Set of Common Divisors
答案为 \(\gcd(A,B)\) 的质因数数量 \(+ 1\)
E.Get Everything
状压dp， 设状态 \(dp_{mask}\) 为得到 \(mask\) 所示状态宝物的最小花费，
显然转移方程为
其中 \(tmp\) 为当前钥匙所对应宝物的状态
F.Pure
进行 \(n\) 次 \(DFS\) 寻找最小环即可，在搜索的过程中记录前驱和到源点的距离
