小白的经典CNN复现(二):LeNet-5
小白的经典CNN复现(二):LeNet-5
各位看官大人久等啦!我胡汉三又回来辣(不是
最近因为到期末考试周,再加上老板临时给安排了个任务,其实LeNet-5的复现工作早都搞定了,结果没时间写这个博客,今天总算是抽出时间来把之前的工作简单总结了一下,然后把这个文章简单写了一下。
因为LeNet-5这篇文章实在是太——长——了,再加上内容稍稍有那么一点点复杂,所以我打算大致把这篇博客分成下面的部分:
-
论文怎么读:因为太多,所以论文里面有些部分可以选择性略过
-
论文要点简析:简单说一下这篇文章中提出了哪些比较有意思的东西,然后提一下这个论文里面有哪些坑
-
具体分析与复现:每一个部分是怎么回事,应该怎么写代码
-
结果简要说明:对于复现的结果做一个简单的描述
-
反思:虽然模型很经典,但是实际上还是有很多的考虑不周的地方,这些也是后面成熟的模型进行改进的地方
在看这篇博客之前,希望大家能先满足下面的两个前置条件:
-
对卷积神经网络的大致结构和功能有一定的了解,不是完完全全的小白
-
对Pytorch有初步的使用经验,不需要特别会,但起码应该知道大致有什么功能
-
LeNet-5这篇论文要有,可以先不读,等到下面讲完怎么读之后再读也没问题
那么废话少说,开始我们的复现之旅吧(@^▽^@)ノ
顺便一提,因为最近老是在写报告、论文还有文献综述啥的,文章风格有点改不回来了,所以要是感觉读着不如以前有意思了,那······凑合读呗,你还能打死我咋的┓( ´∀` )┏
论文该怎么读?
这篇论文的篇幅。。。讲道理当时我看到页码的时候我整个人是拒绝的······然后瞅了一眼introduction部分,发现实际上里面除了介绍他的LeNet-5模型之外,还介绍了如何构建一个完整的文本识别的系统,顺便分析了一下优劣势什么的。也就是说这篇论文里面起码是把两三篇论文放在一起发的,赶明儿我也试试这么水论文┓( ´∀` )┏
因此这篇论文算上参考文献一共45页,可以说对于相关领域的论文来说已经是一篇大部头的文章了。当然实际上关于文本识别系统方面的内容我们可以跳过,因为近年来对于文本识别方面的研究其实比这个里面提到的无论是从精度还是系统整体性能上讲都好了不少。
那这篇论文首先关于导读部分还有文字识别的基本介绍部分肯定是要读的,然后关于LeNet-5的具体结构是什么样的肯定也是要读的,最后就是关于他LeNet-5在训练的时候用到的一些“刀剑神域”操作(我怕系统不让我说SAO这个字),是在文章最后的附录里面讲的,所以也是要看的。把这些整合一下,对应的页码差不多是下面的样子啦:
-
1-5:文本识别以及梯度下降简介
-
5-9:LeNet-5结构介绍
-
9-11:数据集以及训练结果分析
-
40-45:附录以及参考文献
基本上上面的这些内容看完,这篇文章里面关于LeNet-5的内容就能全都看完了,其他的地方如果感兴趣的话自己去看啦,我就不管了哈(滑稽.jpg
在看下面的内容之前,我建议先把上面我说到的那些页码里面的内容先大致浏览一下,要不然下面我写的东西你可能不太清楚我在说什么,所以大家加把劲,先把论文读一下呗。(原来我就是加把劲骑士(大雾)
论文要点简析
这篇论文的东西肯定算是特别特别早了,毕竟1998年的老古董嘛(那我岂不是更老······话说我好像暴露年龄了欸······)。实际上这里面有一些思想已经比较超前了,虽然受当时的理论以及编程思路的限制导致实现得并不好,但是从思路方面上我觉得绝对是有学习的价值的,所以下面我们就将这些内容简单来说一说呗:
-
首先是关于全连接网络为啥不好。在文章中主要提到下面的两个问题:
-
全连接网络并没有平移不变性和旋转不变性。平移不变性和旋转不变性,通俗来讲就是说,如果给你一张图上面有一个东西要识别,对于一个具有平移不变性和旋转不变性的系统来说,不管这张图上的这个东西如何做平移和旋转变换,系统都能把这个东西辨识出来。具体为什么全连接网络不存在平移不变性和旋转不变性,可以参考一下我之前一直在推荐的《Deep Learning with Pytorch》这本书,里面讲的也算是清晰易懂吧,这里就不展开说了;
-
全连接网络由于要把图片展开变成一个行/列向量进行处理,这会导致图片像素之间原有的拓扑结构遭到破坏,毕竟对于图片来讲,一个像素和他周围的像素之间的关系肯定是很密切的嘛,要是不密切插值不就做不了了么┓( ´∀` )┏
-
-
在卷积神经网络结构方面,也提出了下面的有意思的东西:
-
池化层:前面提到过全连接网络不存在平移不变性,而从原理上讲,卷积层是平移不变的。为了让整个辨识系统的平移不变性更加健壮,可以引入池化层将识别出的特征的具体位置再一次模糊化,从而达到系统的健壮性的目的。嘛······这个想法我觉的挺好而且挺超前的,然而,LeCun大佬在这里的池化用的是平均池化······至于这有什么问题,emmmmm,等到后面的反思里面再说吧,这里先和大家提个醒,如果有时间的话可以停下来先想一想为啥平均池化为啥不好。
-
特殊设计的卷积层:在整个网络中间存在一个贼恶心的层,对你没看错,就是贼恶心。当然啦,这个恶心是指的复现层面的,从思路上讲还是有一些学习意义的。这个卷积层不像其他的卷积层,使用前面一层输出的所有的特征图来进行卷积,他是挑着来的,这和我的上一篇的LeNet-1989提到的那个差不多。这一层的设计思想在于:1)控制参数数量防止过拟合(这其实就有点像是完全确定的dropout,而真正的dropout是在好几年以后才提出的,是不是很超前吖);2)破坏对称性;3)强制让卷积核学习到不同的特征。从第一条来看,如果做到随机的话那和dropout就差不多了;第二条的话我没太看明白,如果有大佬能够指点一下的话那就太好了;第三条实际上就是体现了想要尽可能减少冗余卷积核从而减少参数数量的思想,相当于指明了超参数的一个设置思路。
-
RBF层与损失函数:通过向量距离来表征损失,仔细分析公式的话,你会发现,他使用的这个 层加上设计的损失函数,和我们现在在分类问题中常用的交叉熵函数(CrossEntropyLoss)其实已经非常接近了,在此之前大家使用的都是那种one-hot或者基于位置编码的损失函数,从原理性上讲已经是一个很大的进步了······虽然RBF本身因为计算向量距离的缘故,实际上把之前的平移不变性给破坏了······不过起码从思路上讲已经好很多了。
-
特殊的激活函数:这个在前一篇LeNet-1989已经提到过了,这里就不展开说了,有兴趣可以看一下论文的附录部分还有我的上一篇关于LeNet-1989的介绍。
-
初始化方法:这个也在之前一篇的LeNet-1989提到过了,大家就到之前的那一篇瞅瞅(顺便给我增加点阅读量,滑稽.jpg
-
以上就是论文里面一些比较有意思并且有价值的思想和内容,当然了这里只是针对那些刚刚简单看过一遍论文的小伙伴们看的,是想让大家看完论文以后对一些可能一晃就溜过去的内容做个提醒,所以讲得也很简单。如果上面的内容确实是有没注意到的,那就再回去把这些内容找到看一看;如果上面的内容都注意到了,哇那小伙伴你真的是棒!接下来就跟着我继续往下看,把一些很重要的地方进行一些更细致的研读吧(⁎˃ᴗ˂⁎)
具体分析与复现
现在我们假设大家已经把论文好好地看过一遍了,但是对于像我一样的新手小白来说,有一些内容可能看起来很简单,但是实际操作起来完全不知道该怎么搞,所以这里就和大家一起来一点一点扣吧。
首先先介绍一下我复现的时候使用的大致软件和硬件好了:python: 3.6.x,pytorch: 1.4.1, GPU: 1080Ti,window10和Ubuntu都能运行,只需要把文件路径改成对应操作系统的格式就行
在开始写代码之前,同样的,把我们需要的模块啥的,一股脑先都装进来,免得后面有什么东西给忘记了:
import torch
import torch.nn as nn
import torch.optim as optim
from torchvision import datasets
from torchvision import transforms as T
import matplotlib.pyplot as plt
import numpy as np
接下来我们开始介绍复现过程,论文的描述是先说的网络结构,然后再讲的数据集,但是其实从逻辑上讲,我们先搞清楚数据是什么个鬼样子,才知道网络应该怎么设计嘛。所以接下来我们先介绍数据集的处理,再介绍网络结构。
数据集的处理部分
这里使用的就是非常经典的MNIST数据集啦,这个数据集就很好找了,毕竟到处都是,而且也不是很大,拿来练手是再合适不过的了(柿子肯定是挑软的捏,饭肯定专挑软的吃,滑稽.jpg)。一般来说为了让训练效果更好,都需要对数据进行一些预处理,使数据的分布在一个合适的范围内,让训练过程更加高效准确。
在介绍怎么处理数据之前,还是先简单介绍一下这个数据集的特点吧。MNIST数据集中的图片的尺寸为[28, 28],并且都是单通道的灰度图,也就是里面的字都是黑白的。灰度图的像素范围为[0, 255],并且全都是整数。
由于在这个网络结构中使用的激活函数都是和Tanh或者Sigmoid函数十分接近的,为了能让训练过程总体上都在激活函数的线性区中,需要将数据的像素数值分布从之前的[0, 255]转换成均值为0,方差为1的一个近似区间。为了达到这个效果,论文提出可以把图片的像素值范围转换为[-0.1, 1.175],也就是说背景的像素值均为-0.1,有字的最亮的像素值为1.175,这样所有图片的像素值就近似在均值为0,方差为1的范围内了。
除此之外,论文还提到为了让之后的最后一层的感受野能够感受到整个数字,需要将这个图片用背景颜色进行“填充”。注意这里就有两个需要注意的地方:
-
填充:也就是说我们不能简单地用PIL库或者是opencv库中的resize函数,因为这是将图片的各部分进行等比例的插值缩放,而填充的实际含义和卷积层的padding十分接近,因此为了方便起见我们就直接在卷积操作中用padding就好了,能省事就省点事。
-
用背景填充:在卷积进行padding的时候,默认是使用0进行填充,而这和我们的实际的要求是不一样的,因此我们需要对卷积的padding模式进行调整,这个等到到时候讲卷积层的时候再详细说好了。
因此考虑到上面的因素,我们的图片处理器应该长下面的这个鬼样子:
picProcessor = T.Compose([
T.ToTensor(),
T.Normalize(
mean = [0.1 / 1.275],
std = [1.0 / 1.275]
),
])
具体里面的参数都是什么意思,我已经在以前的博客里面提到过了,所以这里就不赘述了哦。图片经过这个处理之后,就变成了尺寸为[28, 28],像素值范围[-0.1, 1.175]的tensor了,然后如何填充成一个[32, 32]的图片,到后面的卷积层的部分再和大家慢慢说。
数据处理完,就加载一下吧,这里和之前的LeNet-1989的代码基本上就一样的吖,就不多解释了。
dataPath = "F:\\Code_Set\\Python\\PaperExp\\DataSetForPaper\\" #在使用的时候请改成自己实际的MNIST数据集路径
mnistTrain = datasets.MNIST(dataPath, train = True, download = False, transform = picProcessor) #记得如果第一次用的话把download参数改成True
mnistTest = datasets.MNIST(dataPath, train = False, download = False, transform = picProcessor)
同样的,如果有条件的话,大家还是在GPU上训练吧,因为这个网络结构涉及到一些比较复杂的中间运算,如果用CPU训练的话那是真的慢,反正我在我的i7-7700上面训练,完整训练下来大概一天多?用GPU就几个小时,所以如果实在没条件的话,就跟着我把代码敲一遍,看懂啥意思就行了,这个我真的没办法┓( ´∀` )┏
device = torch.device("cuda:0") if torch.cuda.is_available() else torch.device("cpu")
网络结构部分
LeNet-5的结构其实还是蛮经典的,不过在这里还是再为大家截一下图,然后慢慢解释解释每层是怎么回事吧。
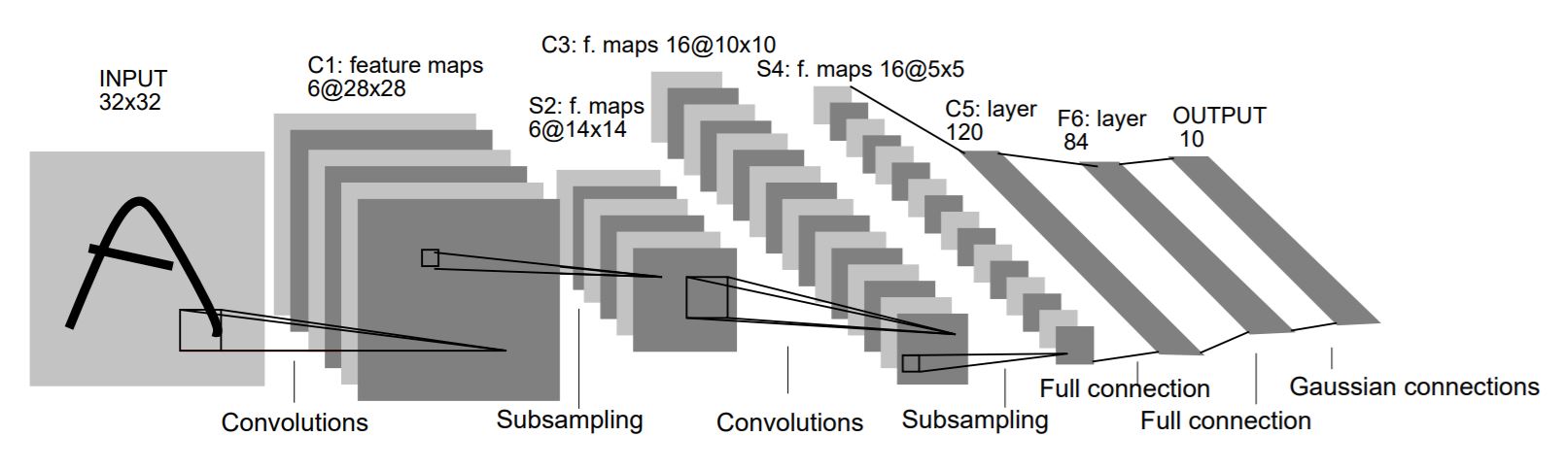
因为这里面的东西其实蛮多的,我怕像上一篇一样在最后才把代码一下子放出来会让人记不住前面讲过啥,所以这部分就每一个结构下面直接跟上对应的代码好了。
整体
我们的神经网络类的名字就定义为LeNet-5好了,大致定义方法如下:
class LeNet-5(nn.Module):
def __init__(self):
super(LeNet-5, self).__init__()
self.C1 = ...
self.S2 = ...
self.C3 = ...
self.S4 = ...
self.C5 = ...
self.F6 = ...
self.Output = ...
self.act = ...
初始化部分...
def forward(self, x):
......
那接下来我们就一个部分一个部分开始看吧。
C1层
C1层就是一个很简单的我们平常最常见的卷积层,然后我们分析一下这一层需要的参数以及输入输出的尺寸。
-
输入尺寸:在不考虑batch_size的情况下,论文中提到的输入图片的尺寸应该是[c, h, w] = [1, 32, 32],但是前面提到,我们为了不在图片处理中花费太大功夫进行图片的填充,需要把图片的填充工作放在卷积操作的padding中。从尺寸去计算的话,padding的维度应该是2,这样就能把实际图片的高宽尺寸从[28, 28]填充为[32, 32]。但是padding的默认参数是插入0,并不是用背景值 -0.1 进行填充,所以我们需要在定义卷积核的时候,将padding_mode这个参数设置为 ’replicate‘,这个参数的意思是,进行padding的时候,会把周围的背景值进行复制赋给padding的维度。
-
输出尺寸:在不考虑batch_size的情况下,输出的特征图的尺寸应该是[c, h, w] = [6, 28, 28]
-
参数:从输入尺寸还有输出尺寸并结合论文的描述上看,使用的卷积参数应该如下:
- in_channel: 1
- out_channel: 6
- kernel_size: 5
- stride: 1
- padding: 2
- padding_mode: 'replicate'
将上面的内容整合起来的话,C1层的构造代码应该是下面的样子:
self.C1 = nn.Conv2d(1, 6, 5, padding = 2, padding_mode = 'replicate')
在这一层的后面没有激活函数哟,至少论文里没有提到。
S2层
S2层以及之后所有的以S开头的层全都是论文里面提到的采样层,也就是我们现在常说的池化层。论文中提到使用的池化层是平均池化,池化层的概念和运作原理,大家还是去查一下其他的资料看一看吧,要不然这一篇篇幅就太长了······但是需要注意的是,这里使用的平均池化和实际我们现在常见的平均池化是不一样的。常见的池化层是,直接将对应的位置的值求个平均值,但是这里很恶心,这里是有权重和偏置的平均求和,差不多就是下面这个样子:
这俩参数w和b还是可训练参数,每一个特征图用的还不是同一个参数,真的我看到这里是拒绝的,明明CNN里面平均池化就不适合用,他还把平均池化搞得这么复杂,吔屎啦你(╯‵□′)╯︵┻━┻
但是自己作的死,跪着也要作完,所以大家就一起跟着我吔屎吧······
在Pytorch里,除了可以使用框架提供的API里面的池化层之外,我们也可以去自定义一个类来实现我们自己需要的功能。当然如果想要这个自定义的类能够和框架提供的类一样运行的话,需要让这个类继承torch.nn.Module这个类,只有这样我们的自定义类才有运算、自动求导等正常功能。并且相关的功能的实现,需要我们自己重写forward方法,这样在调用自己写的类的对象的时候,系统就会通过内置的__call__方法来调用这个forward方法,从而实现我们想要的功能。
下面我们构建一个类Subsampling来实现我们的池化层:
class Subsampling(nn.Module)
首先看一下我们的初始化函数:
def __init__(self, in_channel):
super(Subsampling, self).__init__()
self.pool = nn.AvgPool2d(2)
self.in_channel = in_channel
F_in = 4 * self.in_channel
self.weight = nn.Parameter(torch.rand(self.in_channel) * 4.8 / F_in - 2.4 / F_in, requires_grad=True)
self.bias = nn.Parameter(torch.rand(self.in_channel), requires_grad=True)
这个函数中的参数含义其实一目了然,并且其中也有一些我们在上一篇的LeNet-1989中提到过的让人感觉熟悉的内容,但是······这个多出来的Parameter是什么鬼啦(╯‵□′)╯︵┻━┻。别急别急,我们来一点点的看一下吧。
对于父类的初始化函数调用没什么好说的。我们先来看下面的这一行:
self.pool = nn.AvgPool2d(2)
我们之所以定义 self.pool 这个成员,是因为从上面我们的那个池化层的公式上来看,我们完全可以先对我们要求解的区域先求一个平均池化,再对这个结果做一个线性处理,从数学上是完全等价的,并且这也免得我们自己实现相加功能了,岂不美哉?(脑补一下三国名场景)。并且在论文中指定的池化层的核的尺寸是[2, 2],所以有了上面的定义方法。
然后是下面的和那个Parameter相关的代码:
self.weight = nn.Parameter(torch.rand(self.in_channel) * 4.8 / F_in - 2.4 / F_in, requires_grad=True)
self.bias = nn.Parameter(torch.rand(self.in_channel), requires_grad=True)
从参数的名称上看我们很容易知道weight和bias就是我们的可学习权重和偏置,但是为什么我们需要定义一个Parameter,而不是像以前一样只使用一个tensor完事?这里就要简单介绍一下nn.Module这个类了。在这个类中有三个比较重要的字典:
-
_parameters:模型中的参数,可求导
-
_modules:模型中的子模块,就类似于在自定义的网络中加入的Conv2d()等
-
_buffer:模型中的buffer,在其中的内容是不可自动求导的,常常用来存一些常量,并且在之后C3层的构造中要用到。
当我们向一个自定义的模型类中加入一些自定义的参数的时候(比如上面的weight),我们必须将这个参数定义为Parameter,这样在进行self.weight = nn.Parameter(...)这个操作的时候,pytorch会将这个参数注册到我们上面提到的字典中,这样在后续的反向传播过程中,这个参数才会被计算梯度。当然这里只是十分简单地说一下,详细的内容的话推荐大家看两篇博客,链接放在下面:
https://blog.csdn.net/u012436149/article/details/78281553
https://www.cnblogs.com/zhangxiann/p/13579624.html
然后代码里面的初始化方法什么的,在前一篇LeNet-1989里面已经提到过了,就不多说了。
接下来是forward函数的实现:
def forward(self, x):
x = self.pool(x)
outs = [] #对每一个channel的特征图进行池化,结果存储在这里
for channel in range(self.in_channel):
out = x[:, channel] * self.weight[channel] + self.bias[channel] #这一步计算每一个channel的池化结果[batch_size, height, weight]
outs.append(out.unsqueeze(1)) #把channel的维度加进去[batch_size, channel, height, weight]
return torch.cat(outs, dim = 1)
在这里比较需要注意的部分是for函数以及return部分的内容,我们同样一块一块展开进行分析:
for channel in range(self.in_channel):
out = x[:, channel] * self.weight[channel] + self.bias[channel]
outs.append(out.unsqueeze(1))
前面提到过,我们在每一个前面输出的特征图上计算平均池化的时候,使用的可训练参数都是不一样的,都需要各自进行训练,因此我们需要做的是把每一个channel的特征图都取出来,然后做一个池化操作,所有的channel都池化完毕之后我们再拼回去。
假设我们的输入的尺寸为x = [batch_size, c, h, w],我们的操作步骤应该是这样的:
-
那么我们需要做的是把每一个channel的特征图取出来,也就是x[:, channel] = [batch_size, h, w];
-
对取出来的特征图做池化:out = x[:, channel] * self.weight[channel] + self.bias[channel]
-
把特征图先放在一起(拼接是在return里面做的,这里只是先放在一起),为了让我们的图能够拼起来,需要把池化的输出结果升维,把channel的那一维加进去。之前我们提到out的维度是[batch_size, h, w],channel应该加在第一维上,也就是outs.append(out.unsqueeze(1))
unsqueeze操作也在以前的博客中有写过,就不多说了。
接下来是return的部分
return torch.cat(outs, dim=1)
在这里出现了一个新的函数cat,这个函数的实际作用是,将给定的tensor的列表,沿着dim指定的维度进行拼接,这样我们重新得到的返回值的维度就回复为[batch_size, c, h, w]了。具体的函数用法可以先看看官方文档,然后再自己实践一下,不是很难理解的。
至此Subsampling类就构建完毕了,每个部分都搞清楚以后,我们把类里面所有的代码都拼到一起看一下吧:
class Subsampling(nn.Module):
def __init__(self, in_channel):
super(Subsampling, self).__init__()
self.pool = nn.AvgPool2d(2)
self.in_channel = in_channel
F_in = 4 * self.in_channel
self.weight = nn.Parameter(torch.rand(self.in_channel) * 4.8 / F_in - 2.4 / F_in, requires_grad = True)
self.bias = nn.Parameter(torch.rand(self.in_channel), requires_grad = True)
def forward(self, x):
x = self.pool(x)
outs = [] #对每一个channel的特征图进行池化,结果存储在这里
for channel in range(self.in_channel):
out = x[:, channel] * self.weight[channel] + self.bias[channel] #这一步计算每一个channel的池化结果[batch_size, height, weight]
outs.append(out.unsqueeze(1)) #把channel的维度加进去[batch_size, channel, height, weight]
return torch.cat(outs, dim = 1)
每一个小部分都搞清楚以后再来看这个整体,是不是就清楚多啦!如果还有地方不太明白的话,可以把这部分代码多读几遍,然后多查一查官方的文档,这个里面基本是没有什么特别难的地方的。
这里是定义一个这样的池化层的类,用于复用,因为后面的S4的原理和这个是一致的,只是输入输出的维度不太一样。对于S2来说,先不考虑batch_size,由于从C1输出的尺寸为[6, 28, 28],因此我们进行定义时是按照如下方法定义的:
self.S2 = Subsampling(6)
并且从池化层的核的尺寸来看,得到的池化的输出最终的尺寸为[6, 14, 14]。
需要注意的是,在这一层后面有一个激活函数,但这里有一个小小的问题,论文里写的激活函数是Sigmoid,但我用的不是,具体原因后面再说。
C3层
好家伙刚送走一个麻烦的家伙,现在又来一个。这部分就是之前在 “论文要点简析” 部分提到的花里胡哨的特殊设计的卷积层啦。讲道理写到现在我都感觉我腱鞘炎要犯了······
在介绍这部分代码之前,还是先对整个结构的输入输出以及基本的参数进行简单的分析:
-
输入尺寸:在前一层S2的输出尺寸为[6, 14, 14]
-
输出尺寸:要求的输出尺寸是[16, 10, 10]
-
卷积层参数:要求的卷积核尺寸是[5, 5],没有padding填充,所以在这一层的基本的参数是下面这样的:
- in_channel: 6
- out_channel: 16
- kernel_size: 5
- stride: 1
- padding: 0
但是实际上不能只是这样简单的定义一个卷积层,因为一般的卷积是在输入的全部特征图上进行卷积操作,但是在这个论文里的C3层很 “刀剑神域”,他是每一个输出的特征图都只挑了输入的特征图里的一小部分进行卷积操作,具体的映射关系看下面啦:
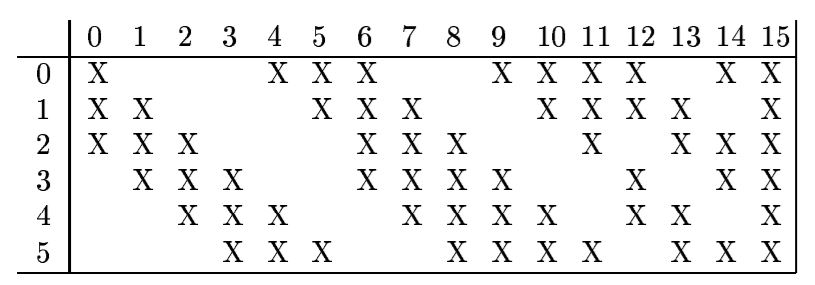
具体来说,这张图的含义是这个样子的:
-
所有的特征图的标号都是从零开始的,输出特征图16个channel,也就是0-15,输入特征图6个channel,也就是0-5
-
竖着看,0号输出特征图,在0、1、2号输入特征图上打了X,也就是说,0号输出特征图是使用0、1、2号输入特征图,在这个图像上进行卷积操作
-
其他的输出特征图同理
因此我们需要提前先定义一个用来表示映射关系的表,然后从表里面挑出来输入特征图进行卷积操作,最后再把得到的输出特征图拼起来,实际上听起来和刚刚的Subsampling类的基本逻辑差不多,就是多了一个映射关系而已。所以下面我们来构造一下这个类吧:
class MapConv(nn.Module):
同样的,我们先从构造方法开始一点点的看这个类。
def __init__(self, in_channel, out_channel, kernel_size = 5):
super(MapConv, self).__init__()
#定义特征图的映射方式
mapInfo = [[1, 0, 0, 0, 1, 1, 1, 0, 0, 1, 1, 1, 1, 0, 1, 1],
[1, 1, 0, 0, 0, 1, 1, 1, 0, 0, 1, 1, 1, 1, 0, 1],
[1, 1, 1, 0, 0, 0, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1],
[0, 1, 1, 1, 0, 0, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1],
[0, 0, 1, 1, 1, 0, 0, 1, 1, 1, 1, 0, 1, 1, 0, 1],
[0, 0, 0, 1, 1, 1, 0, 0, 1, 1, 1, 1, 0, 1, 1, 1]]
mapInfo = torch.tensor(mapInfo, dtype = torch.long)
self.register_buffer("mapInfo", mapInfo) #在Module中的buffer中的参数是不会被求梯度的
self.in_channel = in_channel
self.out_channel = out_channel
self.convs = {} #将每一个定义的卷积层都放进这个字典
#对每一个新建立的卷积层都进行注册,使其真正成为模块并且方便调用
for i in range(self.out_channel):
conv = nn.Conv2d(mapInfo[:, i].sum().item(), 1, kernel_size)
convName = "conv{}".format(i)
self.convs[convName] = conv
self.add_module(convName, conv)
这个里面就用到了我们之前提到的在Module里面重要的三个字典中的剩下两个,可能对于萌新小伙伴来说,这段代码初看起来真的复杂地要死,所以这里我们来一点点地解读这个函数。
首先,对于调用父类进行初始化,然后定义我们的映射信息这些部分我们就不看了,没啥看头,重点是我们来看一下下面这一行代码:
self.register_buffer("mapInfo", mapInfo)
在前面说三大字典的时候我们提到过,在Module的_buffer中的参数是不会被求导的,可以看成是常量。但是如果直接定义一个量放在Module里面的话,他实际上并没有被放在_buffer中,因此我们需要调用从Module类中继承得到的register_buffer方法,来将我们定义的mapInfo强制注册到_buffer这个字典中。
接下来比较重要的是下面的for循环部分:
for i in range(self.out_channel):
conv = nn.Conv2d(mapInfo[:, i].sum().item(), 1, kernel_size)
convName = "conv{}".format(i)
self.convs[convName] = conv
self.add_module(convName, conv)
为什么不能像之前那样一个一个定义卷积层呢?很简单,因为这里如果一个一个做的话,要自己定义16个卷积层,而且到写forward函数中,还要至少写16次输出······反正我是写不来,如果有铁头娃想这么写的话可以去试一下,那滋味一定是酸爽得要死┓( ´∀` )┏
首先是关于每一个单独的卷积层的定义部分:
conv = nn.Conv2d(mapInfo[:, i].sum().item(), 1, kernel_size)
前面我们提到,C3卷积层中的每一个特征图都是从前面的输入里面挑出几个来做卷积的,并且讲那个映射图的时候说过要一列一列地读,也就是说卷积层的输入的通道数in_channels是由mapInfo里面每一列有几个 “1”(X)决定的。
接下来是整个循环的剩余部分:
convName = "conv{}".format(i)
self.convs[convName] = conv
self.add_module(convName, conv)
这部分看起来稍稍有一点复杂,但实际上逻辑还是蛮简单的。在我们自定义的Module的子类中,如果里面有其他的Module子类作为成员(比如Conv2d),那么框架会将这个子类的实例化对象的对象名作为key,实际对象作为value注册到_module中,但是由于这里我们使用的是循环,所以卷积层的对象名就只有conv一个。
为了解决这个问题,我们可以自行定义一个字典convs,然后将自行定义的convName作为key,实际对象作为value,放到这个自定义的字典里面。但是放到这个字典还是没有被注册进_module里面,因此我们需要用从Module类中继承的add_module()方法,将(convName,conv)作为键值对注册到字典里面,这样我们才能在forward方法中,直接调用convs字典中的内容用来进行卷积计算。详细的关于这部分的说明还是参考一下我在上面提到的两个博客的链接。
解释完这个函数之后,接下来是forward函数:
def forward(self, x):
outs = [] #对每一个卷积层通过映射来计算卷积,结果存储在这里
for i in range(self.out_channel):
mapIdx = self.mapInfo[:, i].nonzero().squeeze()
convInput = x.index_select(1, mapIdx)
convOutput = self.convs['conv{}'.format(i)](convInput)
outs.append(convOutput)
return torch.cat(outs, dim = 1)
我们还是直接来看for循环里面的部分,其实这部分如果是有numpy基础的人会觉得很简单,但是毕竟这是面向小白和萌新的博客,所以就稍微听我啰嗦一下吧。
由于我们在看mapInfo的时候是按列看的,也就是说为了取到每一个输出特征图对应的输入特征图,我们应该把mapInfo每一列的非零元素的下标取出来,也就是mapInfo[:, i].nonzero()。nonzero这个函数的返回值是调用这个函数的tensor里面的,所有非零元素的下标,并且每一个非零点下标自成一维。举个例子的话,对mapInfo的第0列,调用nonzero的结果应该是:
[[0], [1], [2]],shape:[3, 1]
之所以要在后面加一个squeeze,是因为后续的index_select函数,这个操作要求要求后面对应的下标序列必须是一个一维的,也就是说需要把[[0], [1], [2]]变成[0, 1, 2],从shape:[3, 1]变成shape:[3],因此需要一个squeeze操作进行压缩。
接下来就是刚刚才提到的index_select操作,这个函数实际上是下面这个样子:
index_select(dim, index)
还有一些其他参数就不列出来了,这个函数的功能是,在指定的dim维度上,根据index指定的索引,将对应的所有元素进行一个返回。
对于我们编写的函数来说,x的shape是[batch_size, c, h, w],而我们需要从里面找到的是从mapInfo中找到的所有非零的channel,也就是说我们需要指定dim=1,也就是convInput = x.index_select(1, mapIdx)
剩下的内容就和之前介绍的Subsampling的内容差不多了,同样的对于每一组输入得到一组卷积,然后最后把所有卷积结果拼起来。
那现在我们把这个类的完整的代码放在一起好啦:
class MapConv(nn.Module):
def __init__(self, in_channel, out_channel, kernel_size = 5):
super(MapConv, self).__init__()
#定义特征图的映射方式
mapInfo = [[1, 0, 0, 0, 1, 1, 1, 0, 0, 1, 1, 1, 1, 0, 1, 1],
[1, 1, 0, 0, 0, 1, 1, 1, 0, 0, 1, 1, 1, 1, 0, 1],
[1, 1, 1, 0, 0, 0, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1],
[0, 1, 1, 1, 0, 0, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1],
[0, 0, 1, 1, 1, 0, 0, 1, 1, 1, 1, 0, 1, 1, 0, 1],
[0, 0, 0, 1, 1, 1, 0, 0, 1, 1, 1, 1, 0, 1, 1, 1]]
mapInfo = torch.tensor(mapInfo, dtype = torch.long)
self.register_buffer("mapInfo", mapInfo) #在Module中的buffer中的参数是不会被求梯度的
self.in_channel = in_channel
self.out_channel = out_channel
self.convs = {} #将每一个定义的卷积层都放进这个字典
#对每一个新建立的卷积层都进行注册,使其真正成为模块并且方便调用
for i in range(self.out_channel):
conv = nn.Conv2d(mapInfo[:, i].sum().item(), 1, kernel_size)
convName = "conv{}".format(i)
self.convs[convName] = conv
self.add_module(convName, conv)
def forward(self, x):
outs = [] #对每一个卷积层通过映射来计算卷积,结果存储在这里
for i in range(self.out_channel):
mapIdx = self.mapInfo[:, i].nonzero().squeeze()
convInput = x.index_select(1, mapIdx)
convOutput = self.convs['conv{}'.format(i)](convInput)
outs.append(convOutput)
return torch.cat(outs, dim = 1)
考虑到我们在开头提到的输入输出尺寸以及参数,最后我们应该做的定义如下所示:
self.C3 = MapConv(6, 16, 5)
和C1一样,这一层的后面也是没有激活函数的。
S4层
这个就很简单啦,就是把我们之前定义的Subsampling类拿过来用就行了,这里就说一下输入输出的尺寸还有参数好啦:
-
输入尺寸:C3的输出:[16, 10, 10]
-
输出尺寸:根据池化的核的大小,尺寸应该为[16, 5, 5]
-
参数:从输入的通道数判断,in_channel = 16
写出来的话应该是:
self.S4 = Subsampling(16)
这一层后面有激活函数,出现的问题和S2层一样,原因之后说
C5层
这个也好简单哟啊哈哈哈哈哈,再复杂下去我可能就要被逼疯了。
和C1层一样,这里是一个简单的卷积层,我们来分析一下输入输出尺寸以及定义参数:
-
输入尺寸:[16, 5, 5]
-
输出尺寸:[120, 1, 1]
-
参数:
- in_channel: 16
- out_channel: 120
- kernel_size: 5
- stride: 1
- padding: 0
写出来的话应该是这样的:
self.C5 = nn.Conv2d(16, 120, 5)
这里同样没有激活函数
F6层
这个也好简单啊哈哈哈哈哈(喂?120吗,这里有个疯子麻烦你们来处理一下)
这里是一个简单的线性全连接层,我们看到上一层的输入尺寸为[120, 1, 1],而线性层在不考虑batch_size的时候,要求输入维度不能这么多,这就需要用到view函数进行维度的重组,当然啦我们这一部分可以放到forward函数里面,这里我们就直接定义一个线性层就好啦:
self.F6 = nn.Linear(120, 84)
这里有一个激活函数,使用的就是和之前的LeNet-1989一样的:
Output层
终于要到最后了,我的妈啊,除了本科毕设我还是头一次日常写东西写这么多的,可把我累坏了。本来还想着最后一层能让人歇歇,结果发现最后一层虽然逻辑很简单,但是从代码行数来看真是恶心得一匹,因为里面涉及到一些数字编码的问题。总之我们先往下看一看吧。
这一层的操作也是“刀剑神域” 得不得了,论文在设计这一层的时候实际上相当于是在做一个特征匹配的工作。论文是将0-9这十个数字的像素编码提取出来,然后将这个像素编码展开形成一个向量。在F6层我们知道输出的向量的尺寸是[84],这个Output层的任务,就是求解F6层输出向量,和0-9的每一个展开成行向量的像素编码求一个平方和的距离,保证这个是一个正值。从结果上讲,如果这个距离是0,那就说明输出向量和该数字对应的行向量完全匹配。距离越小证明越接近,也就是概率越大;距离越大就证明越远离,也就是概率越低。
可能只是这么说有一点点不太好理解,我们来举个例子说明也许会更容易说明一些。我们先来看一下 “1”这个数字的编码大概长什么样子。为了让大家看得比较清楚,本来应该是黑色是+1,白色是-1,我这边就写成黑色是1,白色是0好了。
[0, 0, 0, 1, 1, 0, 0],
[0, 0, 1, 1, 1, 0, 0],
[0, 1, 1, 1, 1, 0, 0],
[0, 0, 0, 1, 1, 0, 0],
[0, 0, 0, 1, 1, 0, 0],
[0, 0, 0, 1, 1, 0, 0],
[0, 0, 0, 1, 1, 0, 0],
[0, 0, 0, 1, 1, 0, 0],
[0, 0, 0, 1, 1, 0, 0],
[1, 1, 1, 1, 1, 1, 1],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0]
仔细看一下里面是 1 的部分,是不是拼起来就像一个印刷体的数字 “1”,当然了你可以把这个矩阵用opencv、PIL或者matplotlib读取然后画出来,确实是印刷体的“1”。然后把它展开形成一个行向量,就是我们用来进行识别的基准模式了。
然后对于这一层的输出,使用的距离函数是下面的样子:
实际就是距离嘛,只不过就是没有开根号而已。
在这层中需要注意的就只有一个点,那就是数字的行向量组成的这个矩阵是固定死的,也就是说和之前的MapConv层中的mapInfo一样是不可训练的常量。
因为这一部分只是代码比较多而已,但是实际上逻辑上很简单,所以这里就不讲解了,直接上代码:
_zero = [-1, +1, +1, +1, +1, +1, -1] + \
[-1, -1, -1, -1, -1, -1, -1] + \
[-1, -1, +1, +1, +1, -1, -1] + \
[-1, +1, +1, -1, +1, +1, -1] + \
[+1, +1, -1, -1, -1, +1, +1] + \
[+1, +1, -1, -1, -1, +1, +1] + \
[+1, +1, -1, -1, -1, +1, +1] + \
[+1, +1, -1, -1, -1, +1, +1] + \
[-1, +1, +1, -1, +1, +1, -1] + \
[-1, -1, +1, +1, +1, -1, -1] + \
[-1, -1, -1, -1, -1, -1, -1] + \
[-1, -1, -1, -1, -1, -1, -1]
_one = [-1, -1, -1, +1, +1, -1, -1] + \
[-1, -1, +1, +1, +1, -1, -1] + \
[-1, +1, +1, +1, +1, -1, -1] + \
[-1, -1, -1, +1, +1, -1, -1] + \
[-1, -1, -1, +1, +1, -1, -1] + \
[-1, -1, -1, +1, +1, -1, -1] + \
[-1, -1, -1, +1, +1, -1, -1] + \
[-1, -1, -1, +1, +1, -1, -1] + \
[-1, -1, -1, +1, +1, -1, -1] + \
[-1, +1, +1, +1, +1, +1, +1] + \
[-1, -1, -1, -1, -1, -1, -1] + \
[-1, -1, -1, -1, -1, -1, -1]
_two = [-1, +1, +1, +1, +1, +1, -1] + \
[-1, -1, -1, -1, -1, -1, -1] + \
[-1, +1, +1, +1, +1, +1, -1] + \
[+1, +1, -1, -1, -1, +1, +1] + \
[+1, -1, -1, -1, -1, +1, +1] + \
[-1, -1, -1, -1, +1, +1, -1] + \
[-1, -1, +1, +1, +1, -1, -1] + \
[-1, +1, +1, -1, -1, -1, -1] + \
[+1, +1, -1, -1, -1, -1, -1] + \
[+1, +1, +1, +1, +1, +1, +1] + \
[-1, -1, -1, -1, -1, -1, -1] + \
[-1, -1, -1, -1, -1, -1, -1]
_three = [+1, +1, +1, +1, +1, +1, +1] + \
[-1, -1, -1, -1, -1, +1, +1] + \
[-1, -1, -1, -1, +1, +1, -1] + \
[-1, -1, -1, +1, +1, -1, -1] + \
[-1, -1, +1, +1, +1, +1, -1] + \
[-1, -1, -1, -1, -1, +1, +1] + \
[-1, -1, -1, -1, -1, +1, +1] + \
[-1, -1, -1, -1, -1, +1, +1] + \
[+1, +1, -1, -1, -1, +1, +1] + \
[-1, +1, +1, +1, +1, +1, -1] + \
[-1, -1, -1, -1, -1, -1, -1] + \
[-1, -1, -1, -1, -1, -1, -1]
_four = [-1, +1, +1, +1, +1, +1, -1] + \
[-1, -1, -1, -1, -1, -1, -1] + \
[-1, -1, -1, -1, -1, -1, -1] + \
[-1, +1, +1, -1, -1, +1, +1] + \
[-1, +1, +1, -1, -1, +1, +1] + \
[+1, +1, +1, -1, -1, +1, +1] + \
[+1, +1, -1, -1, -1, +1, +1] + \
[+1, +1, -1, -1, -1, +1, +1] + \
[+1, +1, -1, -1, +1, +1, +1] + \
[-1, +1, +1, +1, +1, +1, +1] + \
[-1, -1, -1, -1, -1, +1, +1] + \
[-1, -1, -1, -1, -1, +1, +1]
_five = [-1, +1, +1, +1, +1, +1, -1] + \
[-1, -1, -1, -1, -1, -1, -1] + \
[+1, +1, +1, +1, +1, +1, +1] + \
[+1, +1, -1, -1, -1, -1, -1] + \
[+1, +1, -1, -1, -1, -1, -1] + \
[-1, +1, +1, +1, +1, -1, -1] + \
[-1, -1, +1, +1, +1, +1, -1] + \
[-1, -1, -1, -1, -1, +1, +1] + \
[+1, +1, -1, -1, -1, +1, +1] + \
[-1, +1, +1, +1, +1, +1, -1] + \
[-1, -1, -1, -1, -1, -1, -1] + \
[-1, -1, -1, -1, -1, -1, -1]
_six = [-1, -1, +1, +1, +1, +1, -1] + \
[-1, +1, +1, -1, -1, -1, -1] + \
[+1, +1, -1, -1, -1, -1, -1] + \
[+1, +1, -1, -1, -1, -1, -1] + \
[+1, +1, +1, +1, +1, +1, -1] + \
[+1, +1, +1, -1, -1, +1, +1] + \
[+1, +1, -1, -1, -1, +1, +1] + \
[+1, +1, -1, -1, -1, +1, +1] + \
[+1, +1, +1, -1, -1, +1, +1] + \
[-1, +1, +1, +1, +1, +1, -1] + \
[-1, -1, -1, -1, -1, -1, -1] + \
[-1, -1, -1, -1, -1, -1, -1]
_seven = [+1, +1, +1, +1, +1, +1, +1] + \
[-1, -1, -1, -1, -1, +1, +1] + \
[-1, -1, -1, -1, -1, +1, +1] + \
[-1, -1, -1, -1, +1, +1, -1] + \
[-1, -1, -1, +1, +1, -1, -1] + \
[-1, -1, -1, +1, +1, -1, -1] + \
[-1, -1, +1, +1, -1, -1, -1] + \
[-1, -1, +1, +1, -1, -1, -1] + \
[-1, -1, +1, +1, -1, -1, -1] + \
[-1, -1, +1, +1, -1, -1, -1] + \
[-1, -1, -1, -1, -1, -1, -1] + \
[-1, -1, -1, -1, -1, -1, -1]
_eight = [-1, +1, +1, +1, +1, +1, -1] + \
[+1, +1, -1, -1, -1, +1, +1] + \
[+1, +1, -1, -1, -1, +1, +1] + \
[+1, +1, -1, -1, -1, +1, +1] + \
[-1, +1, +1, +1, +1, +1, -1] + \
[+1, +1, -1, -1, -1, +1, +1] + \
[+1, +1, -1, -1, -1, +1, +1] + \
[+1, +1, -1, -1, -1, +1, +1] + \
[+1, +1, -1, -1, -1, +1, +1] + \
[-1, +1, +1, +1, +1, +1, -1] + \
[-1, -1, -1, -1, -1, -1, -1] + \
[-1, -1, -1, -1, -1, -1, -1]
_nine = [-1, +1, +1, +1, +1, +1, -1] + \
[+1, +1, -1, -1, +1, +1, +1] + \
[+1, +1, -1, -1, -1, +1, +1] + \
[+1, +1, -1, -1, -1, +1, +1] + \
[+1, +1, -1, -1, +1, +1, +1] + \
[-1, +1, +1, +1, +1, +1, +1] + \
[-1, -1, -1, -1, -1, +1, +1] + \
[-1, -1, -1, -1, -1, +1, +1] + \
[-1, -1, -1, -1, +1, +1, -1] + \
[-1, +1, +1, +1, +1, -1, -1] + \
[-1, -1, -1, -1, -1, -1, -1] + \
[-1, -1, -1, -1, -1, -1, -1]
RBF_WEIGHT = np.array([_zero, _one, _two, _three, _four, _five, _six, _seven, _eight, _nine]).transpose()
class RBFLayer(nn.Module):
def __init__(self, in_features, out_features, init_weight = None):
super(RBFLayer, self).__init__()
if init_weight is not None:
self.register_buffer("weight", torch.tensor(init_weight))
else:
self.register_buffer("weight", torch.rand(in_features, out_features))
def forward(self, x):
x = x.unsqueeze(-1)
x = (x - self.weight).pow(2).sum(-2)
return x
这样在定义Output层的时候可以使用下面的代码:
self.Output = RBFLayer(84, 10, RBF_WEIGHT)
到这里我们整个神经网络LeNet-5的基本结构就就定义完毕了,然后初始化部分实际上和LeNet-1989是一致的,在这里就不多讲解了。
损失函数和激活函数
在神经网络的结构定义完成之后,我们还需要定义激活函数,要不然我们的LeNet-5的forward函数没有办法写嘛。前面我们提到,卷积层都没有激活函数,池化层都有Sigmoid函数,F6层后面有一个特殊的Tanh函数。这样做其实是可以的,但是我不知道为啥啊,按照论文这样去训练的话,要么损失函数基本不动,要么干脆直接不断增加然后爆炸······所以这里为了契合后面的训练方法,并且让我们的模型能正常训练出来,这俩我们前面所有的Sigmoid函数就都用那个特殊的Tanh函数来代替:
self.act = nn.Tanh()
同样的,我们将系数放到forward里面再加,现在先不用管。
这样我们的神经网络的forward函数也可以写一下啦:
def forward(self, x):
x = self.C1(x)
x = 1.7159 * self.act(2 * self.S2(x) / 3)
x = self.C3(x)
x = 1.7159 * self.act(2 * self.S4(x) / 3)
x = self.C5(x)
x = x.view(-1, 120)
x = 1.7159 * self.act(2 * self.F6(x) / 3)
out = self.Output(x)
return out
而对于损失函数,论文提到,就是使用Output层的输出。什么意思呢?在不考虑batch_size的情况下,我们的Output层的输出应该是一个[10]的向量,每一个值就对应着输入样本到 0-9 的其中一个数字编码向量的距离。假设我们输入的图片是0,然后Output层的输出是[7, 6, 4, 38, 1, 3, 54, 32, 64, 31],那么对应的损失函数值就是对应的实际类别的距离值,也就是out[0] = 7。
现在我们结合着这个损失函数以及Output层的计算思路,如果有接触过一些关于机器学习和深度学习的分类方法的话,应该能判断出来,这个和在分类问题中的交叉熵损失已经很像了,交叉熵损失的计算其实就是一个log_softmax + NLLoss嘛,虽然在这个LeNet-5中并不是用的log_softmax,而是直接用的距离,不过从思路上讲,跳出了以前常用的位置编码以及one-hot向量,这一点已经是相当超前了啊。
那这样看的话,实际上损失函数就只是一个简单的切片索引操作,代码其实很简单,就不详细讲了,直接上代码好啦。
def loss_fn(pred, label):
if(label.dim() == 1):
return pred[torch.arange(pred.size(0)), label]
else:
return pred[torch.arange(pred.size(0)), label.squeeze()]
现在我们终于把和网络结构部分的所有代码都搞定啦!往回一看发现内容是真的多,这也是为什么这一部分我决定每一部分都把原理和代码全都放在一起,要是把代码和原理分开,我估计代码敲着敲着就不知道该写哪里了。这一部分的内容还是蛮重要的,如果觉得有点混乱的话,最好还是反复多看几遍。下面就是整个神经网络结构的完整代码啦:
class LeNet5(nn.Module):
def __init__(self):
super(LeNet5, self).__init__()
self.C1 = nn.Conv2d(1, 6, 5, padding = 2, padding_mode = 'replicate')
self.S2 = Subsampling(6)
self.C3 = MapConv(6, 16, 5)
self.S4 = Subsampling(16)
self.C5 = nn.Conv2d(16, 120, 5)
self.F6 = nn.Linear(120, 84)
self.Output = RBFLayer(84, 10, RBF_WEIGHT)
self.act = nn.Tanh()
for m in self.modules():
if isinstance(m, nn.Conv2d):
F_in = m.kernel_size[0] * m.kernel_size[1] * m.in_channels
m.weight.data = torch.rand(m.weight.data.size()) * 4.8 / F_in - 2.4 / F_in
elif isinstance(m, nn.Linear):
F_in = m.in_features
m.weight.data = torch.rand(m.weight.data.size()) * 4.8 / F_in - 2.4 / F_in
def forward(self, x):
x = self.C1(x)
x = 1.7159 * self.act(2 * self.S2(x) / 3)
x = self.C3(x)
x = 1.7159 * self.act(2 * self.S4(x) / 3)
x = self.C5(x)
x = x.view(-1, 120)
x = 1.7159 * self.act(2 * self.F6(x) / 3)
out = self.Output(x)
return out
训练函数部分
训练函数部分和之前的LeNet-1989相比基本没有什么变化,所以这里我们先把整个代码放上来:
def train(epochs, model, optimizer, scheduler: bool, loss_fn, trainSet, testSet):
trainNum = len(trainSet)
testNum = len(testSet)
for epoch in range(epochs):
lossSum = 0.0
print("epoch: {:02d} / {:d}".format(epoch+1, epochs))
for idx, (img, label) in enumerate(trainSet):
x = img.unsqueeze(0).to(device)
y = torch.tensor([label], dtype = torch.long).to(device)
out = model(x)
optimizer.zero_grad()
loss = loss_fn(out, y)
loss.backward()
optimizer.step()
lossSum += loss.item()
if (idx + 1) % 2000 == 0: print("sample: {:05d} / {:d} --> loss: {:.4f}".format(idx+1, trainNum, loss.item()))
lossList.append(lossSum / trainNum)
with torch.no_grad():
errorNum = 0
for img, label in trainSet:
x = img.unsqueeze(0).to(device)
out = model(x)
_, pred_y = out.min(dim = 1)
if(pred_y != label): errorNum += 1
trainError.append(errorNum / trainNum)
errorNum = 0
for img, label in testSet:
x = img.unsqueeze(0).to(device)
out = model(x)
_, pred_y = out.min(dim = 1)
if(pred_y != label): errorNum += 1
testError.append(errorNum / testNum)
if scheduler == True:
if epoch < 5:
for param_group in optimizer.param_groups:
param_group['lr'] = 1.0e-3
elif epoch < 10:
for param_group in optimizer.param_groups:
param_group['lr'] = 5.0e-4
elif epoch < 15:
for param_group in optimizer.param_groups:
param_group['lr'] = 2.0e-4
else:
for param_group in optimizer.param_groups:
param_group['lr'] = 1.0e-4
torch.save(model.state_dict(), 'F:\\Code_Set\\Python\\PaperExp\\LeNet-5\\epoch-{:d}_loss-{:.6f}_error-{:.2%}.pth'.format(epochs, lossList[-1], testError[-1]))
我们可以发现,和上一篇的LeNet-1989的训练函数比较,就只有一些小地方不太一样:
- 由于论文里面,训练集和测试集的错误率都被评估了,所以这里比之前的部分多了一个对训练集的错误率计算;
- 之前由于我们使用的输出是和one-hot进行比较,因此我们判断样本的对应标签的时候使用的是max(),但是由于在这里我们是基于向量距离来判断样本的标签,所以实际上在这里要使用min()来获取实际标签
在上一篇中,我并没有说这个后面的if判断里面的代码到底是怎么回事,所以这里就来大致讲一下:
在训练神经网络的时候会用到各种各样的优化器,并且在初始化优化器的时候我们常常会使用下面这样的语句:
optimizer = optim.Adam(model.parameters(), lr=0.001)
实际上当这样定义之后,框架就会将所有的相关参数,存到优化器内部的一个字典param_group里面,并且由于optimizer里面可能会有很多组参数,所以里面还有一个更大的字典param_groups,里面是所有的param_group。这样当我们想要调整学习率的时候,就可以在每一次训练结束之后,通过遍历这两个字典,来将所有的和训练相关的参数进行自定义的调整。
当然实际上还有一些类可以专门用于调整学习率,但是在这里不太好用,所以我就自己写了一下,大家有兴趣可以去查一下相关的资料,很容易找的。
这里还有一个和论文不太一样的地方就是,论文里面的学习率调整其实蛮复杂的,他大概是这样调的:
-
指定一个常数μ=0.02
-
每一个epoch先给一个基准的学习率ε
-
每经过一定数量的样本,累计计算二阶导数h
-
每次进行梯度下降的时候使用的实际学习率为
就是这么恶心,所以这里我就省点事,不计算二阶导数了,直接就按照他的ε的下降规律进行训练好啦(这也有可能是我训练效果不如论文里面的原因吧)
那么现在我们关于整个模型的构建以及训练等相关部分就都讲完了,接下来,添加一些简单的可视化工作,然后把代码全部都拼到一起吧:
import torch
import torch.nn as nn
import torch.optim as optim
from torchvision import datasets
from torchvision import transforms as T
from torch.utils.data import DataLoader
import matplotlib.pyplot as plt
import numpy as np
'''
定义数据的初始化方法:
1. 将数据转化成tensor
2. 将数据的灰度值范围从[0, 1]转化为[-0.1, 1.175]
3. 将数据进行尺寸变化的操作我们放在卷积层的padding操作中,这样更加方便
'''
picProcessor = T.Compose([
T.ToTensor(),
T.Normalize(
mean = [0.1 / 1.275],
std = [1.0 / 1.275]
),
])
'''
数据的读取和处理:
1. 从官网下载太慢了,所以先重新指定路径,并且在mnist.py文件里把url改掉
2. 使用上面的处理器进行MNIST数据的处理,并加载
3. 将每一张图片的标签转换成one-hot向量
'''
dataPath = "F:\\Code_Set\\Python\\PaperExp\\DataSetForPaper\\" #在使用的时候请改成自己实际的MNIST数据集路径
mnistTrain = datasets.MNIST(dataPath, train = True, download = False, transform = picProcessor)
mnistTest = datasets.MNIST(dataPath, train = False, download = False, transform = picProcessor)
# 因为如果在CPU上,模型的训练速度还是相对来说较慢的,所以如果有条件的话就在GPU上跑吧(一般的N卡基本都支持)
device = torch.device("cuda:0") if torch.cuda.is_available() else torch.device("cpu")
'''
神经网络类的定义
1. C1(卷积层): in_channel = 1, out_channel = 6, kernel_size = (5, 5), stride = 1, 我们在这里将图片进行padding放大:
padding = 2, padding_mode = 'replicate', 含义是用复制的方式进行padding
2. 激活函数: 无
3. S2(下采样,即池化层):kernel_size = (2, 2), stride = (2, 2), in_channel = 6, 采用平均池化,根据论文,加权平均权重及偏置也可训练
4. 激活函数:1.7159Tanh(2/3 * x)
5. C3(卷积层): in_channel = 6, out_channel = 16, kernel_size = (5, 5), stride = 1, padding = 0, 需要注意的是,这个卷积层
需要使用map进行一个层次的选择
6. 激活函数: 无
7. S4(下采样,即池化层):和S2基本一致,in_channel = 16
8. 激活函数: 同S2
9. C5(卷积层): in_channel = 16, out_channel = 120, kernel_size = (5, 5), stride = 1, padding = 0
10. 激活函数: 无
11. F6(全连接层): 120 * 84
12. 激活函数: 同S4
13. output: RBF函数,定义比较复杂,直接看程序
无激活函数
按照论文的说明,需要对网络的权重进行一个[-2.4/F_in, 2.4/F_in]的均匀分布的初始化
由于池化层和C3卷积层和Pytorch提供的API不一样,并且RBF函数以及损失函数Pytorch中并未提供,所以我们需要继承nn.Module类自行构造
'''
# 池化层的构造
class Subsampling(nn.Module):
def __init__(self, in_channel):
super(Subsampling, self).__init__()
self.pool = nn.AvgPool2d(2) #先做一个平均池化,然后直接对池化结果做一个加权
#这个从数学公式上讲和对池化层每一个单元都定义一个相同权重值是等价的
self.in_channel = in_channel
F_in = 4 * self.in_channel
self.weight = nn.Parameter(torch.rand(self.in_channel) * 4.8 / F_in - 2.4 / F_in, requires_grad = True)
self.bias = nn.Parameter(torch.rand(self.in_channel), requires_grad = True)
def forward(self, x):
x = self.pool(x)
outs = [] #对每一个channel的特征图进行池化,结果存储在这里
for channel in range(self.in_channel):
out = x[:, channel] * self.weight[channel] + self.bias[channel] #这一步计算每一个channel的池化结果[batch_size, height, weight]
outs.append(out.unsqueeze(1)) #把channel的维度加进去[batch_size, channel, height, weight]
return torch.cat(outs, dim = 1)
# C3卷积层的构造
class MapConv(nn.Module):
def __init__(self, in_channel, out_channel, kernel_size = 5):
super(MapConv, self).__init__()
#定义特征图的映射方式
mapInfo = [[1, 0, 0, 0, 1, 1, 1, 0, 0, 1, 1, 1, 1, 0, 1, 1],
[1, 1, 0, 0, 0, 1, 1, 1, 0, 0, 1, 1, 1, 1, 0, 1],
[1, 1, 1, 0, 0, 0, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1],
[0, 1, 1, 1, 0, 0, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1],
[0, 0, 1, 1, 1, 0, 0, 1, 1, 1, 1, 0, 1, 1, 0, 1],
[0, 0, 0, 1, 1, 1, 0, 0, 1, 1, 1, 1, 0, 1, 1, 1]]
mapInfo = torch.tensor(mapInfo, dtype = torch.long)
self.register_buffer("mapInfo", mapInfo) #在Module中的buffer中的参数是不会被求梯度的
self.in_channel = in_channel
self.out_channel = out_channel
self.convs = {} #将每一个定义的卷积层都放进这个字典
#对每一个新建立的卷积层都进行注册,使其真正成为模块并且方便调用
for i in range(self.out_channel):
conv = nn.Conv2d(mapInfo[:, i].sum().item(), 1, kernel_size)
convName = "conv{}".format(i)
self.convs[convName] = conv
self.add_module(convName, conv)
def forward(self, x):
outs = [] #对每一个卷积层通过映射来计算卷积,结果存储在这里
for i in range(self.out_channel):
mapIdx = self.mapInfo[:, i].nonzero().squeeze()
convInput = x.index_select(1, mapIdx)
convOutput = self.convs['conv{}'.format(i)](convInput)
outs.append(convOutput)
return torch.cat(outs, dim = 1)
# RBF函数output层的构建
class RBFLayer(nn.Module):
def __init__(self, in_features, out_features, init_weight = None):
super(RBFLayer, self).__init__()
if init_weight is not None:
self.register_buffer("weight", torch.tensor(init_weight))
else:
self.register_buffer("weight", torch.rand(in_features, out_features))
def forward(self, x):
x = x.unsqueeze(-1)
x = (x - self.weight).pow(2).sum(-2)
return x
# 损失函数的构建
def loss_fn(pred, label):
if(label.dim() == 1):
return pred[torch.arange(pred.size(0)), label]
else:
return pred[torch.arange(pred.size(0)), label.squeeze()]
# RBF的初始化权重
_zero = [-1, +1, +1, +1, +1, +1, -1] + \
[-1, -1, -1, -1, -1, -1, -1] + \
[-1, -1, +1, +1, +1, -1, -1] + \
[-1, +1, +1, -1, +1, +1, -1] + \
[+1, +1, -1, -1, -1, +1, +1] + \
[+1, +1, -1, -1, -1, +1, +1] + \
[+1, +1, -1, -1, -1, +1, +1] + \
[+1, +1, -1, -1, -1, +1, +1] + \
[-1, +1, +1, -1, +1, +1, -1] + \
[-1, -1, +1, +1, +1, -1, -1] + \
[-1, -1, -1, -1, -1, -1, -1] + \
[-1, -1, -1, -1, -1, -1, -1]
_one = [-1, -1, -1, +1, +1, -1, -1] + \
[-1, -1, +1, +1, +1, -1, -1] + \
[-1, +1, +1, +1, +1, -1, -1] + \
[-1, -1, -1, +1, +1, -1, -1] + \
[-1, -1, -1, +1, +1, -1, -1] + \
[-1, -1, -1, +1, +1, -1, -1] + \
[-1, -1, -1, +1, +1, -1, -1] + \
[-1, -1, -1, +1, +1, -1, -1] + \
[-1, -1, -1, +1, +1, -1, -1] + \
[-1, +1, +1, +1, +1, +1, +1] + \
[-1, -1, -1, -1, -1, -1, -1] + \
[-1, -1, -1, -1, -1, -1, -1]
_two = [-1, +1, +1, +1, +1, +1, -1] + \
[-1, -1, -1, -1, -1, -1, -1] + \
[-1, +1, +1, +1, +1, +1, -1] + \
[+1, +1, -1, -1, -1, +1, +1] + \
[+1, -1, -1, -1, -1, +1, +1] + \
[-1, -1, -1, -1, +1, +1, -1] + \
[-1, -1, +1, +1, +1, -1, -1] + \
[-1, +1, +1, -1, -1, -1, -1] + \
[+1, +1, -1, -1, -1, -1, -1] + \
[+1, +1, +1, +1, +1, +1, +1] + \
[-1, -1, -1, -1, -1, -1, -1] + \
[-1, -1, -1, -1, -1, -1, -1]
_three = [+1, +1, +1, +1, +1, +1, +1] + \
[-1, -1, -1, -1, -1, +1, +1] + \
[-1, -1, -1, -1, +1, +1, -1] + \
[-1, -1, -1, +1, +1, -1, -1] + \
[-1, -1, +1, +1, +1, +1, -1] + \
[-1, -1, -1, -1, -1, +1, +1] + \
[-1, -1, -1, -1, -1, +1, +1] + \
[-1, -1, -1, -1, -1, +1, +1] + \
[+1, +1, -1, -1, -1, +1, +1] + \
[-1, +1, +1, +1, +1, +1, -1] + \
[-1, -1, -1, -1, -1, -1, -1] + \
[-1, -1, -1, -1, -1, -1, -1]
_four = [-1, +1, +1, +1, +1, +1, -1] + \
[-1, -1, -1, -1, -1, -1, -1] + \
[-1, -1, -1, -1, -1, -1, -1] + \
[-1, +1, +1, -1, -1, +1, +1] + \
[-1, +1, +1, -1, -1, +1, +1] + \
[+1, +1, +1, -1, -1, +1, +1] + \
[+1, +1, -1, -1, -1, +1, +1] + \
[+1, +1, -1, -1, -1, +1, +1] + \
[+1, +1, -1, -1, +1, +1, +1] + \
[-1, +1, +1, +1, +1, +1, +1] + \
[-1, -1, -1, -1, -1, +1, +1] + \
[-1, -1, -1, -1, -1, +1, +1]
_five = [-1, +1, +1, +1, +1, +1, -1] + \
[-1, -1, -1, -1, -1, -1, -1] + \
[+1, +1, +1, +1, +1, +1, +1] + \
[+1, +1, -1, -1, -1, -1, -1] + \
[+1, +1, -1, -1, -1, -1, -1] + \
[-1, +1, +1, +1, +1, -1, -1] + \
[-1, -1, +1, +1, +1, +1, -1] + \
[-1, -1, -1, -1, -1, +1, +1] + \
[+1, +1, -1, -1, -1, +1, +1] + \
[-1, +1, +1, +1, +1, +1, -1] + \
[-1, -1, -1, -1, -1, -1, -1] + \
[-1, -1, -1, -1, -1, -1, -1]
_six = [-1, -1, +1, +1, +1, +1, -1] + \
[-1, +1, +1, -1, -1, -1, -1] + \
[+1, +1, -1, -1, -1, -1, -1] + \
[+1, +1, -1, -1, -1, -1, -1] + \
[+1, +1, +1, +1, +1, +1, -1] + \
[+1, +1, +1, -1, -1, +1, +1] + \
[+1, +1, -1, -1, -1, +1, +1] + \
[+1, +1, -1, -1, -1, +1, +1] + \
[+1, +1, +1, -1, -1, +1, +1] + \
[-1, +1, +1, +1, +1, +1, -1] + \
[-1, -1, -1, -1, -1, -1, -1] + \
[-1, -1, -1, -1, -1, -1, -1]
_seven = [+1, +1, +1, +1, +1, +1, +1] + \
[-1, -1, -1, -1, -1, +1, +1] + \
[-1, -1, -1, -1, -1, +1, +1] + \
[-1, -1, -1, -1, +1, +1, -1] + \
[-1, -1, -1, +1, +1, -1, -1] + \
[-1, -1, -1, +1, +1, -1, -1] + \
[-1, -1, +1, +1, -1, -1, -1] + \
[-1, -1, +1, +1, -1, -1, -1] + \
[-1, -1, +1, +1, -1, -1, -1] + \
[-1, -1, +1, +1, -1, -1, -1] + \
[-1, -1, -1, -1, -1, -1, -1] + \
[-1, -1, -1, -1, -1, -1, -1]
_eight = [-1, +1, +1, +1, +1, +1, -1] + \
[+1, +1, -1, -1, -1, +1, +1] + \
[+1, +1, -1, -1, -1, +1, +1] + \
[+1, +1, -1, -1, -1, +1, +1] + \
[-1, +1, +1, +1, +1, +1, -1] + \
[+1, +1, -1, -1, -1, +1, +1] + \
[+1, +1, -1, -1, -1, +1, +1] + \
[+1, +1, -1, -1, -1, +1, +1] + \
[+1, +1, -1, -1, -1, +1, +1] + \
[-1, +1, +1, +1, +1, +1, -1] + \
[-1, -1, -1, -1, -1, -1, -1] + \
[-1, -1, -1, -1, -1, -1, -1]
_nine = [-1, +1, +1, +1, +1, +1, -1] + \
[+1, +1, -1, -1, +1, +1, +1] + \
[+1, +1, -1, -1, -1, +1, +1] + \
[+1, +1, -1, -1, -1, +1, +1] + \
[+1, +1, -1, -1, +1, +1, +1] + \
[-1, +1, +1, +1, +1, +1, +1] + \
[-1, -1, -1, -1, -1, +1, +1] + \
[-1, -1, -1, -1, -1, +1, +1] + \
[-1, -1, -1, -1, +1, +1, -1] + \
[-1, +1, +1, +1, +1, -1, -1] + \
[-1, -1, -1, -1, -1, -1, -1] + \
[-1, -1, -1, -1, -1, -1, -1]
RBF_WEIGHT = np.array([_zero, _one, _two, _three, _four, _five, _six, _seven, _eight, _nine]).transpose()
#整个神经网络的搭建
class LeNet5(nn.Module):
def __init__(self):
super(LeNet5, self).__init__()
self.C1 = nn.Conv2d(1, 6, 5, padding = 2, padding_mode = 'replicate')
self.S2 = Subsampling(6)
self.C3 = MapConv(6, 16, 5)
self.S4 = Subsampling(16)
self.C5 = nn.Conv2d(16, 120, 5)
self.F6 = nn.Linear(120, 84)
self.Output = RBFLayer(84, 10, RBF_WEIGHT)
self.act = nn.Tanh()
for m in self.modules():
if isinstance(m, nn.Conv2d):
F_in = m.kernel_size[0] * m.kernel_size[1] * m.in_channels
m.weight.data = torch.rand(m.weight.data.size()) * 4.8 / F_in - 2.4 / F_in
elif isinstance(m, nn.Linear):
F_in = m.in_features
m.weight.data = torch.rand(m.weight.data.size()) * 4.8 / F_in - 2.4 / F_in
def forward(self, x):
x = self.C1(x)
x = 1.7159 * self.act(2 * self.S2(x) / 3)
x = self.C3(x)
x = 1.7159 * self.act(2 * self.S4(x) / 3)
x = self.C5(x)
x = x.view(-1, 120)
x = 1.7159 * self.act(2 * self.F6(x) / 3)
out = self.Output(x)
return out
lossList = []
trainError = []
testError = []
#训练函数部分
def train(epochs, model, optimizer, scheduler: bool, loss_fn, trainSet, testSet):
trainNum = len(trainSet)
testNum = len(testSet)
for epoch in range(epochs):
lossSum = 0.0
print("epoch: {:02d} / {:d}".format(epoch+1, epochs))
for idx, (img, label) in enumerate(trainSet):
x = img.unsqueeze(0).to(device)
y = torch.tensor([label], dtype = torch.long).to(device)
out = model(x)
optimizer.zero_grad()
loss = loss_fn(out, y)
loss.backward()
optimizer.step()
lossSum += loss.item()
if (idx + 1) % 2000 == 0: print("sample: {:05d} / {:d} --> loss: {:.4f}".format(idx+1, trainNum, loss.item()))
lossList.append(lossSum / trainNum)
with torch.no_grad():
errorNum = 0
for img, label in trainSet:
x = img.unsqueeze(0).to(device)
out = model(x)
_, pred_y = out.min(dim = 1)
if(pred_y != label): errorNum += 1
trainError.append(errorNum / trainNum)
errorNum = 0
for img, label in testSet:
x = img.unsqueeze(0).to(device)
out = model(x)
_, pred_y = out.min(dim = 1)
if(pred_y != label): errorNum += 1
testError.append(errorNum / testNum)
if scheduler == True:
if epoch < 5:
for param_group in optimizer.param_groups:
param_group['lr'] = 1.0e-3
elif epoch < 10:
for param_group in optimizer.param_groups:
param_group['lr'] = 5.0e-4
elif epoch < 15:
for param_group in optimizer.param_groups:
param_group['lr'] = 2.0e-4
else:
for param_group in optimizer.param_groups:
param_group['lr'] = 1.0e-4
torch.save(model.state_dict(), 'F:\\Code_Set\\Python\\PaperExp\\LeNet-5\\epoch-{:d}_loss-{:.6f}_error-{:.2%}.pth'.format(epochs, lossList[-1], testError[-1]))
if __name__ == '__main__':
model = LeNet5().to(device)
optimizer = optim.SGD(model.parameters(), lr = 1.0e-3)
scheduler = True
epochs = 25
train(epochs, model, optimizer, scheduler, loss_fn, mnistTrain, mnistTest)
plt.subplot(1, 3, 1)
plt.plot(lossList)
plt.subplot(1, 3, 2)
plt.plot(trainError)
plt.subplot(1, 3 ,3)
plt.plot(testError)
plt.show()
结果简要分析
我写到这里真的有点头痛了······所以我就偷个懒,结果的曲线就不画了,直接说一个结果好了。
最终这个模型训练,在训练25轮之后,损失函数值为5.0465(论文并未提及),在训练集的错误率为1.2%(论文为0.35%),在测试集上的错误率为2.1%(论文为0.95%),不过考虑到他的学习率的下降方式并未被完美还原,再加上训练25轮的时候模型其实还有收敛的空间,只不过因为当时突然有点别的工作所以电脑要腾出来干别的没得办法继续训练了,所以其实模型的性能还能再通过训练提高。不过就复现工作本身,我觉得已经差不多可以了吧,嗯,就当时这样好了┓( ´∀` )┏
结果反思
总体来说这篇论文很多地方非常值得学习,主要存在以下几个方面吧:
- 卷积结构的提出,这个虽然是废话,但是这也告诉我们一个事情,就是神经网络的结构本身还有很多不合理的地方,有待我们继续优化,就比如说卷积结构相较于之前的全连接结构,引入了平移不变性,但是卷积本身仍然不支持旋转不变性,这也是为什么后来的基于卷积的模型,大多数都对训练集进行了随机旋转、镜像变换等数据增强
- 引入了池化概念,虽然在论文中的池化方法并不是很合适,但是这种希望通过模糊化从而将特征的位置信息进行剔除的思想还是十分先进的
- 设计了近似于dropout的卷积层,虽然稍微有一点点那种多此一举的感觉,但是这其实结合现在的一些研究看来,还是有一些继续思考的空间的。比如卷积层的输出通道数out_channels一直是一个不太好选择的超参数,并且在训练中观察卷积的参数变化,其实可以发现卷积层中有许多特征图都是冗余没有必要的。其实在这篇LeNet-5的论文中就蕴含着一种思想,就是既然有冗余特征,那我干脆强制让特征图学一些特征,这样不就不冗余了嘛,而且可以顺便把参数量降下来。其实从优化角度上讲,这种想法还是蛮有趣的
- 引入了和交叉熵十分接近的损失函数,这就使得进行分类问题的处理的时候,整个模型的性能以及可解释性变得更好了。
- 引入了下降的学习率,对于训练来说,当训练到接近局部最优值的时候,如果学习率还很大那肯定是容易在最优值附近不停地震荡,然后导致模型最终性能不是很好(秘技 · 反复横跳!)。此时降低学习率,将会更容易收敛到最优值附近。
- 引入了随机梯度下降
先不说上面的理论上理解了多少,反正在复现这篇论文的时候,最起码python以及pytorch的编程能力上肯定是提高了不少,而且pytorch的源码阅读经验也肯定是积累了不少┓( ´∀` )┏
整篇论文确实有不少闪光点,但是里面还是有一些不是很好的地方,当然啦这篇文章在当时来看已经是相当优秀了,只是在技术不断发展的现在,再回过头去看这篇文章,多少还是有一点点论文已经落伍了的感觉,并且有一些地方在我个人浅薄的知识量来看,感觉有一点不太对劲:
- 平均池化:论文提到,为了能够使特征的位置参数模糊化,可以使用平均池化进行处理,乍一看感觉好像挺对的,但是接下来我们来举一个例子进行简单说明,假设平均池化就是做个平均值,也不做其他的任何处理了。现在我们假设现在有一个输入向量[48, 0, 0, 0],数值超过24的时候我们认为是某一特征存在,显然从输入来看特征存在,如果是最大池化的话,池化结果为48,特征存在;但是平均池化最终的结果是12,特征不存在。再假设有另一个输入向量[25, 25, 25, 25],最大池化为25,特征存在;平均池化结果为25,特征存在。举这个例子的目的就在于,对于识别问题来说,为了保证不变性,最大池化我感觉效果应该是很好的。这里论文可能是考虑过这个问题所以引入了学习参数,使得特征能够通过学习来得到,但是这个我感觉稍微有一种多此一举的感觉。(当然啦也有可能是我读论文太少,没有看到关于最大池化的缺点的相关论文,如果有大佬在评论区指点一下的话那就更好了)
- dropout的卷积:单纯从减少参数量的角度上讲,这样的设计可能还是挺不错的,如果是想实现一个近似的dropout的功能的话,我觉得其实有一点点没必要,毕竟如果输出特征图在所有的输入特征图上做卷积的话,输入特征图如果不是很重要那么学习到的权重会近似为0,也就达到和这个人为的dropout差不多的效果了。而且由于这个是人工设计的映射模式,那么这个模式到底是否合适?这相当于又引入了新的超参数和人工特征,对于模型的泛化来说可能并不是那么有帮助。不过从卷积结构出发的特殊处理这种思路我觉得还是值得借鉴的。
- RBF层的处理:前面论文里面提到了卷积以及池化,目的实际就是在于让整个网络对于特征的位置信息变得不那么敏感,但是在这一层,又引入了与位置信息强相关的数字编码向量,而且是用输入和这个向量进行距离计算得到分类依据。我觉得这样又把之前好不容易丢掉了的位置信息又捡回来了,当然也有可能是我没能正确理解这一部分的含义,反正我是觉得这里怪怪的。并且,如果是以距离为依据来判断分类依据的话,我觉得不能简单地只是求一个距离,而是应该对输入和数字编码向量先都进行单位化,这样才能将因为向量的模长导致的距离变化的影响降到最低,事实上如果是判断距离的话,我觉得角度是最重要的,而具体的距离长度反而不是那么重要,毕竟这些数字编码向量肯定是线性无关的嘛。
- 随机梯度下降:在前一篇文章中只是简单提了一下,这里稍微细致介绍一下。对于一般的正常的基于所有样本的梯度下降来说,使用的公式大概是这样的:
这样做是最准确的,但是会导致每一次都要计算很多的导数进行相加,而且这么大的计算量还只是计算了更新参数的一小步,每一小步都要计算这么多东西,很明显计算成本是很高的。
仔细观察一下上面的式子,可以发现如果把整个训练集看做一个总体空间,那么取平均相当于是求一个期望,从我们学习过的概率论里面的东西可以知道,如果我们从中取出一部分样本,对样本求均值,那这个均值肯定是实际期望的无偏估计量,而这个实际上就是mini-batch的梯度下降的思想。如果我们进一步极端化,完全可以取其中的一个样本值作为期望来代替,这也就是SGD随机梯度下降。但是大家思考一下,随机梯度下降一次选一个样本是很快,但是这个样本值和实际的期望之间的差距太过于随机了,导致模型很可能朝着完全不合适的方向进行优化,所以合理的使用mini-batch我觉得才是最好的。
从这个描述上也可以看出来,为了引入随机性并且不让计算量太大,batch_size也不能取得太大。
结语
总之从学习来说,这篇论文比较适合拿来做一个对比思考,以及用来熟悉Pytorch的各种操作。反正我是觉得看完这篇论文之后,基本的一些深度学习的概念,以及Pytorch各种模块与类的使用,好多都涉及到了,而且掌握地也稍微比以前好了那么一点点。
当然啦,我也算是一个刚刚入行的小白,可能还是很多的内容说得并不正确,还是希望各位大佬能在评论区批评指正。下一篇打算是复现一下AlexNet,但是ImageNet的数据集一来我不知道从哪里找(官网下载有点慢,如果谁有网盘链接希望能给我一份,不胜感激),二来是这个数据集太大了,130+G,我假期回家以后就家里的破电脑实在是无能为力,所以下一篇重点就放在模型怎么构建上,就不训练了哈,大家感兴趣可以自己搞一搞,我就不弄了。
写了这么多可算是要结束了,突然有点不舍得呢(T_T),如果不出意外的话应该就是更新AlexNet了,那大家下次再见辣!(一看字数快2w,头一次写这么多我真是要吐了)
参考内容:



 浙公网安备 33010602011771号
浙公网安备 33010602011771号