浙大人工智能算法与系统课程作业指南系列(一)再续:口罩识别的神经网络结构
浙大人工智能算法与系统课程作业指南系列(一)再续:口罩识别的神经网络结构
好啦好啦~各位亲爱的小伙伴们,我 JD 又回来辣~为了进一步帮助大家通过这个作业来为以后的AI研究做准备,在这里我打算简单介绍一下课程代码提供的MobileNetV1的代码,虽然挺简单的,我甚至在怀疑干嘛要提供这么个没啥卵用的示例┓( ´∀` )┏。闲话不多说了,我们直接开讲!
为了更加方便小伙伴们读代码,我把里面没啥卵用的注释,以及和模型本身没什么太大关系的部分全都删除了,所以和课程提供的源代码会稍稍有一点点不一样,不过没啥大问题:
import torch
import torch.nn as nn
import torch.nn.functional as F
class MobileNetV1(nn.Module):
def __init__(self, classes=2):
super(MobileNetV1, self).__init__()
self.mobilebone = nn.Sequential(
self._conv_bn(3, 32, 2),
self._conv_dw(32, 64, 1),
)
self.avg_pool = nn.AdaptiveAvgPool2d(1)
self.fc = nn.Linear(64, classes)
for m in self.modules():
if isinstance(m, nn.Conv2d):
n = m.kernel_size[0] * m.kernel_size[1] * m.out_channels
m.weight.data.normal_(0, (2. / n) ** .5)
if isinstance(m, nn.BatchNorm2d):
m.weight.data.fill_(1)
m.bias.data.zero_()
def forward(self, x):
x = self.mobilebone(x)
x = self.avg_pool(x)
x = x.view(x.size(0), -1)
out = self.fc(x)
return out
def _conv_bn(self, in_channel, out_channel, stride):
return nn.Sequential(
nn.Conv2d(in_channel, out_channel, 3, stride, padding=1, bias=False),
nn.BatchNorm2d(out_channel),
nn.ReLU(inplace=True),
)
def _conv_dw(self, in_channel, out_channel, stride):
return nn.Sequential(
nn.Conv2d(in_channel, out_channel, 1, 1, 0, bias=False),
nn.BatchNorm2d(out_channel),
nn.ReLU(inplace=False),
)
这个代码的具体位置是在notebook里面的torch_py/MobileNet.py,很好找啊。很快啊,啪的一下就点开看就完事了。这可能是我这个系列到此为止一次性贴的最多的代码了欸······代码很长,但是我们时间也很长啊,一点点来嘛
在开始读这个MobileNetV1这个类之前,我们先来看看他继承的这个类 nn.Module。其实呢,Pytorch提供了很多神经网络的基本模型,比如全连接模型nn.Linear(),卷积层nn.Conv2d(),还有我们会在下一个作业里面见到的长短期记忆网络nn.LSTM()等等。但是有的时候这些并不能完全满足你的需要,有可能你需要把很多这些子网络组合起来拼成一个大的网络,或者干脆自己写点神奇的结构,那这个时候你就需要自定义一个类,让这个类继承nn.Module,只有这样之后你的自定义网络才能让Pytorch正常地识别并运行。
顺便说一下,和之前两篇文章不一样的是,这回读代码的前置要提及的东西会比较多,如果新的读者比较了解的话,直接往下翻吧,如果是从头跟着读到现在的小萌新们,还是要好好读好好看哈。
在读这个系列的我的随笔的时候,我在第一篇里说了些前提条件,就是说你要对神经网络的基本结构有一些大致的了解,而且下面的内容也会涉及到这些,所以如果大家还没有了解神经网络的基本结构,最好去找些其他文章做个入门,然后再接着回到我的碗里来(滑稽.jpg)。
下面我们要简单介绍一下在这个网络里面接触到的,也是神经网络中最基本的两个结构:线性全连接层(nn.Linear),二维卷积核(nn.Conv2d)。
我们先给出一个十分简单的全连接层的参数列表吧~
nn.Linear(input_size, output_size)
这个参数列表也是和上面代码里基本一致的。下面是一张简单的全连接神经网络的图片: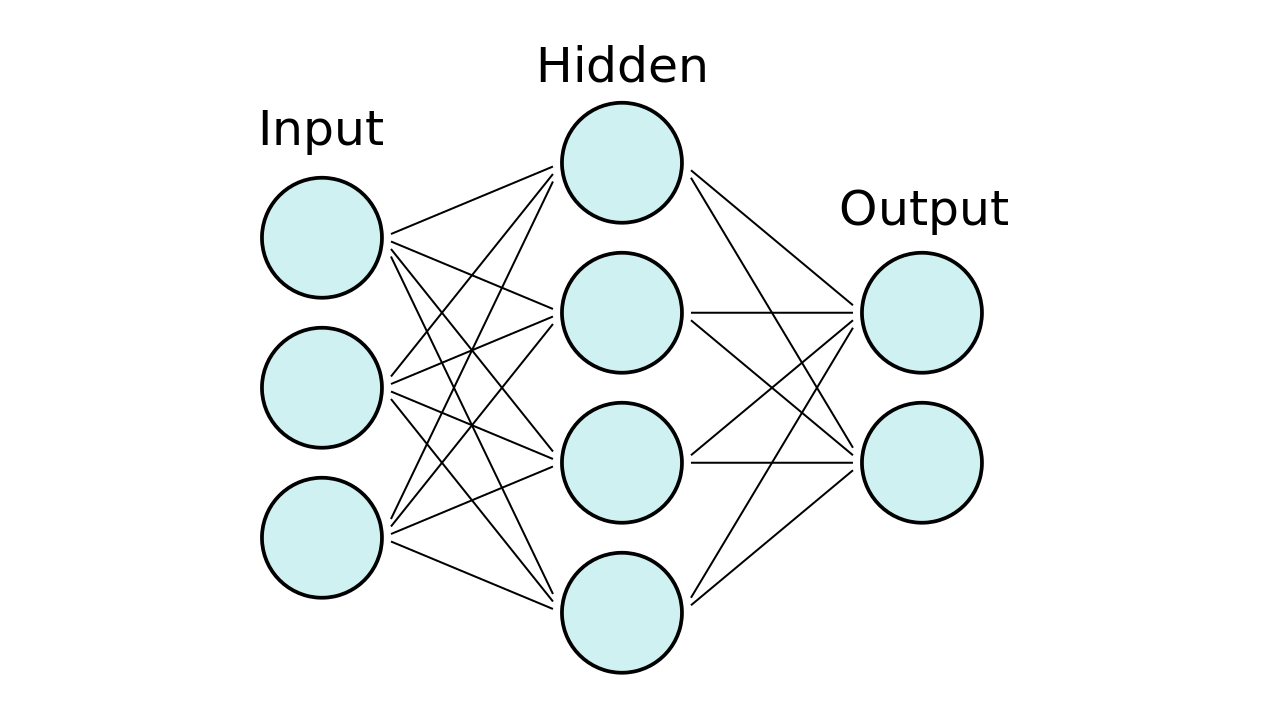
对于全连接层,相信各位小伙伴们并不陌生,如果大家对神经网络稍微有过一些学习的话,大家可能就会知道,神经网络的运算,或者说这些神经层,实际上都是做了矩阵乘法,也就是说实际上上面那幅图就只是一堆的矩阵乘法运算的可视化而已,从这个角度上来看,这个Linear实际上存储的东西应该是下图的红色方框中的部分:

然后通过这个图,我们来看一下Linear层的参数吧~
input_size:Linear的输入端有几个神经元,或者说对应的输入有几个特征
output_size:Linear的输出端有几个神经元,或者说对应的输出有几个特征
以输入层和隐藏层之间的那个Linear为例,input_size = 3,output_size = 4
全连接层就是这么简单,接下来呢我们来看一下卷积层吧~下面是一张输入图片和卷积核的关系:
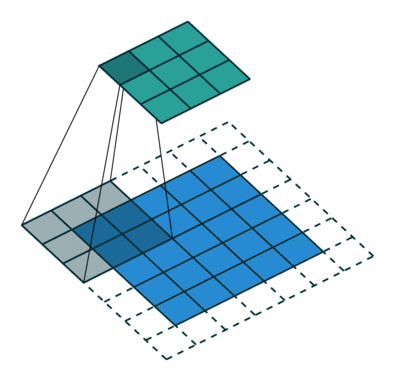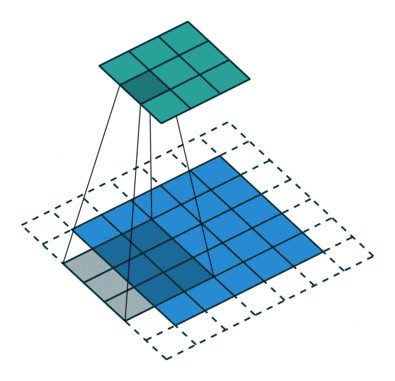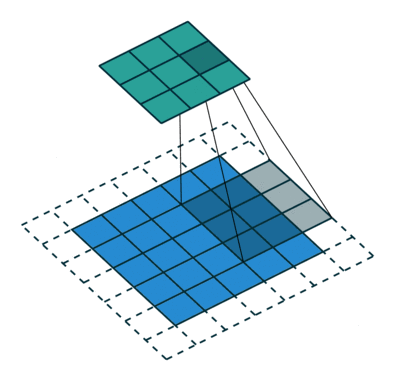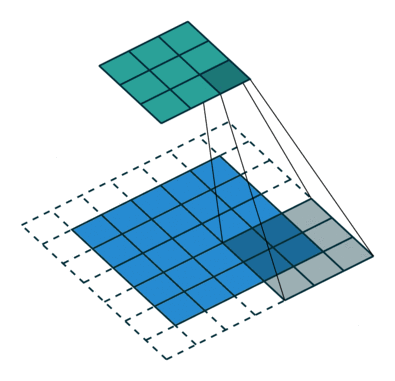
在这个图片里面,下面的蓝色的部分为实际的图片,在蓝色的图片上面有一个灰色的3x3的网格就是我们的卷积核啦~我们可以看到卷积核一般都是一个方形的。卷积运算实际上就是把卷积核上的值和下面图片里面的像素值做一个线性组合,然后把得到的值放到新的图片,也就是最上面的绿色图片的对应位置。为了得到一张新的图,下面蓝色的图片总会大吼一声:“卷积核!上来,自己动”(好快的车车⁄(⁄ ⁄•⁄ω⁄•⁄ ⁄)⁄),然后卷积核就会按照一个给定的步长进行移动,先沿着行,再沿着列。在基本介绍完之后,我们来看一下二维卷积核的API参数列表吧!
nn.Conv2d(in_channel, out_channel, kernel_size, stride, padding, bias)
在Deeping Learning领域里,卷积核的专业术语叫做kernel,这也就是参数里面那个kernel_size里面那个kernel。在第一篇中我们提到过,输入神经网络的图片的尺寸必须是(batch_size, channels, height, width)的尺寸,而卷积核的输入参数in_channel以及out_channel就是对应的图片尺寸中的channels这个维度。
kernel_size这个参数也很好理解,Conv2d默认卷积核是一个正方形的,因此我们传入的这个参数实际上就是这个卷积核的边长。可能有小伙伴就会问了,如果我就是想要一个矩形的咋办?我只想说你是在难为我胖虎(不是),事实上你只需要把你想要的尺寸用(height, width)的元组形式穿进去就好啦。bias这个参数是一个布尔类型,因为我们的卷积运算是一个线性运算类似于wx + b,bias就是设置是否在计算的时候有那个b(我没在骂人!警察叔叔我冤枉啊!)
还剩下两个参数stride和padding没有说,别急嘛,马上就说。stride参数是卷积核移动的步长,在默认情况下卷积核在行列两个移动方向都是等长的,也就是说你输入一个数进去就完事了。如果你非要步长不相等,和上面的kernel_size的处理方法一样,自己动。然后接下来是这个padding,对应上面那个卷积神经网络的图,实际就是蓝色图周围那一圈虚线的小框框。padding的实际作用就是在每一个维度的两端都加上你的padding的值,比如说图片是5x5的,当padding=1的时候,图片会在左右一行的左右+1,一列的上下+1,也就变成了7x7,并且填入的像素值都是0。
小伙伴可能会问了,为啥要加一个这个padding啊?我们先来举个栗子。假设我们的图片是4x4的,卷积核是3x3的,stride = 1,padding = 0。我们会发现通过卷积核的移动,输出的图片尺寸变成了2x2,卷积核在图片上动完以后图片变小了(好家伙这破路都能开,警察叔叔就是这个人!)。而早期的神经网络在设计的时候,希望输入输出的图片尺寸尽量是一致的,所以会用padding操作把原图片变大一点,然后再卷积,就还是和之前一样了。(虽然后来好多模型都是要让图片变小一点)
这个时候我们来读上面神经网络的代码,就会稍微容易一点点咯······大概吧┓( ´∀` )┏
首先是这一段:
self.mobilebone = nn.Sequential(
self._conv_bn(3, 32, 2),
self._conv_dw(32, 64, 1),
)
好家伙上来就当场自闭。我们先来读一下里面两个函数对应的代码,因为里面两个函数对应的代码结构是完全一样的,所以我们就以第一个为例大概说一下:
def _conv_bn(self, in_channel, out_channel, stride):
return nn.Sequential(
nn.Conv2d(in_channel, out_channel, 3, stride, padding=1, bias=False),
nn.BatchNorm2d(out_channel),
nn.ReLU(inplace=True),
)
呐呐,卷积核部分就和我们之前说的一样吧,然后下面还有两个运算,BatchNorm2d的功能主要是对我们的卷积得到的输出做一个批标准化,让我们的输出能够在一个合理的分布区间内,在一定程度上可以加快我们的训练速度,并且稍微降低过拟合的风险,原理就不细说了;而ReLU函数是一个激活函数,实际上是对每一个数值做了这样的一个运算:ReLU(x) = max(0, x),这样的激活函数相较于传统的Sigmoid函数以及Tanh函数来说,运算快,求导容易,而且在一定程度上解决了梯度消失问题。但是这个函数也是存在一些缺陷的,比如由于x < 0时导数为0,所以可能会杀死一部分神经元(没梯度咋更新嘛┓( ´∀` )┏);输出不是以0为中心;数据会不断膨胀等等,具体的还是去参考一些其他大佬的博客好了。
然后这三个部分都被由一个nn.Sequential包了起来,当我们令一个对象net = nn.Sequential(a, b, c)时,我们就相当于将a, b, c打包都归给了net,就组成了一个稍微大一点的子网络。这也顺便解释了一下mobilebone部分的那个代码段。OK我们继续~
self.avg_pool = nn.AdaptiveAvgPool2d(1)
在卷积神经网络中,为了进一步降低我们在网络中的特征数来降低网络参数数量,我们会在卷积之后进行一个池化操作(Pooling),实际上池化也是特殊的卷积,主要目的就是为了降维。在正常来说我们应该用通常的池化操作MaxPool2d(kernel_size, stride),来规定我们在进行池化的时候尺寸还有步长是什么。但是这就需要我们在写代码的时候,自己心里要清楚到每个位置图片输出和输入的尺寸是啥,然后自己算池化的核尺寸以及步长。幸运的是,Pytorch直接帮我们把这个问题解决了,这个AdaptiveAvgPool2d(out_size)的参数,就是你想要输出的图片的最后尺寸(height, width),Pytorch会自动帮你算出来池化的核还有步长。
下面还有一行定义全连接层的代码,这个之前已经讲得很清楚了吧,参数还有可视化的东西都有提到了,还不懂的话建议直接打死,哼╭(╯^╰)╮
下面还有一个对所有的参数进行初始化的一些代码,这些首先从功能上很容易读懂,其次是初始化的方法上稍微涉及到了MobileNetV1的原理上的东西,所以直接Pass。(懒人行为)总之,一个卷积神经网络的基本结构大致上都是这样:好几个卷积层连在一起,然后池化之后后面接一个全连接层,就可以作为最后的输出了,虽然有一些网络不太一样(比如ResNet等),不过大部分都差不多。
然后是这个模型中的非常重要的部分,就是下面的这个函数:
def forward(self, x):
x = self.mobilebone(x)
x = self.avg_pool(x)
x = x.view(x.size(0), -1)
out = self.fc(x)
return out
首先是这个函数本身。在Pytorch中,所有继承了nn.Module的类都会继承其中的方法,其中有一个方法是__call__,这个方法会自动调用类里面的forward方法,并且执行一些其他的功能。也就是说,当你自定义了一个自己的神经网络结构的时候,如果想让这个网络正常运行,一定要在这个类中定义一个forward方法,一定要是这个名字哈。
当我们执行model(x)的时候,就会自行调用forward(x)函数。但是说了这么久,我们输入数据到底是什么样子的呢?emmmmm,如果我们去查看一下我们的数据集中的文件,我们会发现给出的图片都是三通道的,160x160的图片。这个尺寸一定要记住,因为这和下面的我们神经网络的结构有关系。
这个代码的内部结构里面,前两行的mobilebone还有avg_pool的代码都已经讲过了,就不多说了,但是下面的x.view()又是什么呢?在讲这个之前,我们最好先回过头来,看一下我们这个整体的网络里面到底每一层输出的尺寸都是什么,那么下面我就只把和网络结构有关的代码放在一起,并且用注释的方式给出输入输出的图片的尺寸,并且为了方便起见,我们将batch_size用B表示。:
self.mobilebone = nn.Sequential(
#input: [B, 3, 160, 160]
nn._conv_bn(3, 32, 2)
#output: [B, 32, 80, 80]
#input: [B, 32, 80, 80]
nn._conv_dw(32, 64, 1)
#output: [B, 64, 80, 80]
)
#total output: [B, 64, 80, 80]
#input: [B, 64, 80, 80]
self.avg_pool = nn.AdaptiveAvgPool(1)
#output: [B, 64, 1, 1]
#input: [B, 64, 1, 1], 尺寸不对辣~
self.fc = nn.Linear(64, classes = 2)
我们可以发现,当到全连接层那里的时候,根据我们之前的描述,全连接层接受的尺寸应该是[batch_size, input_size = 64]这样的类型,很显然这边多出来两个。萌新小伙伴们可能会再次懵逼,哎呀这可咋办嘛Σ(っ°Д°;)っ。嗯······在介绍view的功能之前,我们最好是先对Pytorch中tensor的存储方式进行简单的介绍。
真要说起来的话,tensor的存储方式和C++数组的存储方式是差不多的,tensor也是要在内存中占据一段连续的存储空间,然后通过数组名来表示数组的首地址,然后通过[]运算符来获取元素的位置,与首地址进行计算之后得到元素的准确位置,进而取值。也就是说,在Pytorch的tensor中,有这样一个思想:不管你一个tensor是啥维度的,底层数据都一模一样,改变的只是我怎么看这个tensor罢了,这个思想很重要。而view(视图)函数就是反应这个思想的一个功能。
虽然数据是一个[B, 64, 1, 1]的数据,但是在底层数据都是按照一个顺序进行顺序存储的,现在我们需要将它转化成[B, 64]的数据,那我把后面两维丢掉不就完事了。然后在view函数的参数其实很有趣,每一个位置就对应的要输出的tensor的维度,比如在第一个出现的数字,就对应着输出的第0维的尺寸;当给出的数字是-1的时候,函数会自动按照其他的维度的尺寸以及tensor的元素个数,自动地帮你算出这个位置的数字,哎呀妈呀贼贴心好吗。
所以在forward函数中的下面的句子:
x = x.view(x.size(0), -1)
本质上讲,就是把图片从[B, 64, 1, 1],转化为[B, s],然后元素个数是B * 64 * 1 * 1 = B * 64,第0维尺寸为B,那s = 64可不是理所当然(MVP:所以爱会消失是吗,大误)
到这里,我们的神经网络基本结构就介绍完了。基本上在理解包括前两篇在内的所有内容之后,如果小伙伴们想自己写一个数据处理步骤、训练函数以及神经网络模型,基本上不会有太大的问题,最多可能就是在一些小的函数使用上查查Pytorch的文档然后学一学。这个作业也就基本上可以写了。但是呢,这个作业其实,还! 有! 坑! 至于是什么坑,我们放在下一篇继续说吧,大家下次见~



 浙公网安备 33010602011771号
浙公网安备 33010602011771号