点是否在三角形内问题的思考

关于点是否在三角形内（落在边线上亦可）问题的解法，大体有两种：

1、根据面积来求解：

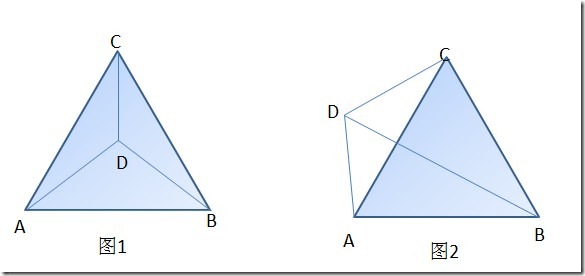
当点D落于三角形内时，图1所示，则由D与A,B,C三个顶点所组成的三个三角形面积之和即为外围三角形面积：S(ABC)=S(ABD)+S(BCD)+S(ACD)

当点D落于三角形外时，图2所示，则由D与A,B,C三个顶点所组成的三个三角形面积之和应该大于原三角形面积之和，多出了面积S(ACD):S(ABC)<S(ABD)+S(BCD)+S(ACD)

而根据三角形三条边长求解面积的公式如下：

假设三条边长为：a、b、c则

p=(a+b+c)/2  =>  S(ABC)=sqrt((p-a)*(p-b)*(p-c)*p);

 

2、根据向量叉积来求解：

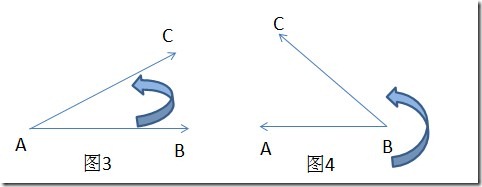
当一个点与一向量的叉积为正时，我们可以确定该点位于当前向量的左边，因为sin<BAC>为正，图3所示;

当一个点与一向量的叉积为负时，我们可以确定该点位于当前向量的右边，因为sin<BAC>为负，图4所示;

 

故，我们可以利用这点来判断点与三角形的关系。

假设向量AD与AB的叉积结果表示为：p(AD，AB)

当点D位于三角形以内时，则延着ABC逆时针走，点D都位于三条边的左侧，也就是说向量AD与AB,向量BD与BC,向量CD与CA的叉积均为正，因为它们之间的夹角均小于180度。图5所示，

则：p(AD，AB)>0&&p(BD，BC)>0&&p(CD，CA)>0

当点D位于三角形外面时，则向量AD与AB,向量BD与BC,向量CD与CA的叉积结果中有一个会为负，比如向量CA与CD的叉积结果，注意夹角是以逆时针旋转得到的，故角ACD大于180度，图6所示，

则：p(AD，AB)>0&&p(BD，BC)>0&&p(CD，CA)>0 结果不成立时则可判断D位于三角形之外。

 

下面给出向量叉积的求解公式：

假如A向量为(a,b),B向量为(c,d),则向量A与B叉积的结果为：a*d-b*c。当结果为正时，则说明两向量间的夹角为0到180度之间，为负时则为180到360之间。

以上两种思路转换成相应的code都比较简单，这里就不详细记录呢。