[笔记] 三元环 && 四元环计数
Thanks to Prutekoi!
三元环计数
无向图的三元环计数
我们首先需要对无向边按一定规则定向:
设 \(in[u]\) 表示 \(u\) 的度数
- 若 \(in[u]<in[v]\) ,从 \(u\) 向 \(v\) 连边,反之则从 \(v\) 向 \(u\) 连边。
- 若 \(in[u]==in[v]\) ,我们从编号小的点向编号大的点连边。
此时这张图是一张有向无环图。
枚举每个点 \(u\) ,标记所有 \(u\) 的出点;然后枚举点 \(u\) 的出点 \(v\) ,再枚举 \(v\) 的出点 \(w\) ,若 \(w\) 被标记,则 \((u,v,w)\) 成三元环。
每个三元环只会在 \(u\) 被统计一次,如下图。
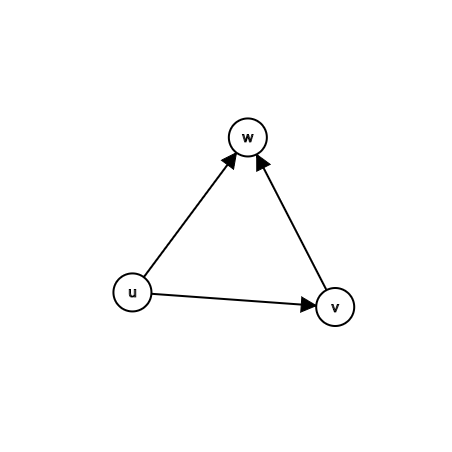
代码:
#define R register int
inline void main() {
n=g(),m=g();
for(R i=1,u,v;i<=m;++i) u=g(),v=g(),++d[u],++d[v],e[i]=edge(u,v);
for(R i=1,u,v;i<=m;++i) { u=e[i].u,v=e[i].v;
if(d[u]>d[v]||(d[u]==d[v]&&u>v) add(u,v);
else add(v,u);
} R ans=0;
for(R u=1;u<=n;++u) { ++C;
for(R i=fir[u];i;i=nxt[i]) flg[vr[i]]=C;
for(R i=fir[u];i;i=nxt[i])
for(R j=fir[vr[i]];j;j=nxt[j]) ans+=(flg[vr[j]]==C);
} printf("%d\n",ans);
}
时间复杂度:
考虑在中间枚举的那个点,贡献为 \(\mathcal{O}(in_u \times out_u),out_u \leq \mathcal{O}(\sqrt{m}),in_u \leq \mathcal{O}(m)\) ,所以复杂度为 \(\mathcal{O}(m\sqrt{m})\) 。
有向完全图(竞赛图)的三元环计数
\(C(n,3)-\sum_{u} C(in_u,2)\) ,\(in_u\) 表示 \(u\) 的入度。
四元环计数
还是要对边定向,同样类似上边的定向。
但此时注意枚举点 \(u\) 相邻的点 \(v\) 是原图中的边(而非重定向后的边),而枚举 \(v\) 相邻的点 \(w\) 则要是重定向后的点(可以交换图的顺序),原因是我们相当于是枚举两个部分拼起来。
还是在 \(u\) 被枚举一次,因为 \(rk[u]<rk[w]\).
代码:
inline bool cmp(const int& _this,const int& _that)
{return d[_this]<d[_that]||(d[_this]==d[_that]&&_this<_that);}
#define con const int&
inline void main() {
n=g(),m=g(); for(R i=1,u,v;i<=m;++i)
u=g(),v=g(),e[u].push_back(v),e[v].push_back(u);
for(R i=1;i<=n;++i) d[id[i]=i]=e[i].size();
sort(id+1,id+n+1,cmp);
for(R i=1;i<=n;++i) rk[id[i]]=i;
for(R u=1;u<=n;++u) for(con v:e[u])
if(rk[v]>rk[u]) f[u].push_back(v);
for(R u=1;u<=n;++u) {
for(con v:e[u]) for(con w:f[v]) if(rk[w]>rk[u]) ans+=c[w],++c[w]; //交换e与f的枚举顺序也是对的。
for(con v:e[u]) for(con w:f[v]) if(rk[w]>rk[u]) c[w]=0; //清空桶。
} printf("%lld\n",ans);
}
时间复杂度:
仍然考虑在中间枚举的点的贡献:\(\mathcal{O}(d_i\times out_i),d_i \leq \mathcal{O}(m),out_i \leq \mathcal{O}(\sqrt{m})\),所以复杂度为 \(\mathcal{O}(m\sqrt{m})\) 。
还有一种别的写法:
const int N=510;
int n,m; ll ans; bitset <N> e[N];
inline void main() {
n=g(),m=g(); for(R i=1,u,v;i<=m;++i) u=g(),v=g(),e[u][v]=true,e[v][u]=true;
for(R i=1,tmp;i<=n;++i) for(R j=i+1;j<=n;++j) {
tmp=(e[i]&e[j]).count(); ans+=tmp*(tmp-1);
} printf("%lld\n",ans>>2);
}
\(\mathcal{O}(n^3/32)\)
思考:其实也可以从度数大的连向度数小的点,但是连边方式会改变,并且复杂度分析会用到 \(in_u\) 。
2019.10.28
upd on 2020.06.11


