已知椭圆长轴，短轴，圆心，旋转角度求任意椭圆外包矩形

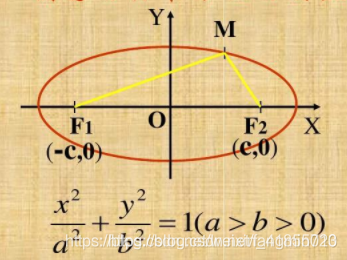
一、已知椭圆长轴，短轴，圆心，旋转角度求椭圆（旋转未做平移）方程一般式：

一般来说，椭圆可以以任何一点为中心，也可以有与坐标轴不平行的轴。这样的椭圆总是可以从标准位置的椭圆开始，然后进行旋转和/或平移得到。对于一般性的公式，我们可以包括通过一个角度为0的旋转(即根本没有旋转)和通过零向量的平移(根本没有平移)来进行变换。也就是说，每一个椭圆都可以通过在标准位置上旋转和平移得到。因此，对椭圆的标准方程进行旋转和平移，可以得到任意椭圆的方程。
是旋转然后平移，还是相反，这是一个需要选择的问题。为了理解这个，让R表示一个旋转，考虑点x = ( x , y ) x=(x,y)x=(x,y)，会发生什么如果我们先平移向量v vv，然后应用 R RR。因为R RR是线性的，变换之后的结果为R ( x + v ) = R x + R v R(x+v)=Rx+RvR(x+v)=Rx+Rv，然而这和先旋转x xx，然后用R v RvRv平移是一样的。这表明，每一个椭圆都可以从一个标准位置的椭圆中得到，要么是旋转后再平移，要么是平移后再旋转。在推导椭圆的一般方程时，我们将使用先旋转后平移的方法。
参考旋转矩阵的两种用法一文，我们使用极坐标工具，绕原点逆时针旋转，通过一个角α αα，很容易可以将( x , y ) (x,y)(x,y)变成( x c o s α − y s i n α , y c o s α + x s i n α ) (xcosα-ysinα,ycosα+xsinα)(xcosα−ysinα,ycosα+xsinα)。写成矩阵的形式为：

然后，再次使用坐标旋转变换公式，即可得到椭圆的长短轴信息，参考Rotated Conic Section Identifying这个视频

二、上述基础上，增加平移向量，方程一般式为：

三、上述基础上增加平移向量，方程一般式为：
1.构造关于x的二元一次方程式：

2.令△=0，构造关于y的二元一次方程组，求得y值为Y最大和最小值。

构造关于y的二元一次方程式，

令△=0，构造关于x的二元一次方程组，求得x值为x最大和最小值。

四、代码实现

static void Main(string[] args)
{
    double maxX = 0, minX = 0, maxY = 0, minY = 0;
    CalcEllipseRect(0.4254, 2.1152, 0, 201.7681, 163.9117, ref maxX, ref minX, ref maxY, ref minY);
    CalcEllipseRect(0.4254, 2.1152, (Math.PI * 3.0 / 4.0 + Math.PI / 6.0), 201.7681, 163.9117, ref maxX, ref minX, ref maxY, ref minY);
    CalcEllipseRect(3.86555, 10.7108, (Math.PI / 4.0), -0.8859, 7.57, ref maxX, ref minX, ref maxY, ref minY);
    Console.WriteLine($"maxX {maxX}, minX {minX}, maxY {maxY}, minY {minY}");
}

/// <summary>
/// 计算椭圆外包矩形
/// </summary>
/// <param name="minorAxis">短轴半径</param>
/// <param name="majorAxis">长轴半径</param>
/// <param name="rotation">旋转角度(弧度)</param>
/// <param name="centerX">椭圆圆心X</param>
/// <param name="centerY">椭圆圆心Y</param>
/// <param name="maxX"></param>
/// <param name="minX"></param>
/// <param name="maxY"></param>
/// <param name="minY"></param>
/// <returns></returns>
static bool CalcEllipseRect(double minorAxis, double majorAxis, double rotation, double centerX, double centerY,
    ref double maxX, ref double minX, ref double maxY, ref double minY)
{
    //计算椭圆方程旋转(未平移)一般式：Ax²+Bxy+Cy²=1。中A,B,C
    double A = (Math.Cos(rotation) * Math.Cos(rotation)) / (majorAxis * majorAxis) + (Math.Sin(rotation) * Math.Sin(rotation)) / (minorAxis * minorAxis);
    double B = 2 * Math.Cos(rotation) * Math.Sin(rotation) * (1.0 / (majorAxis * majorAxis) - 1.0 / (minorAxis * minorAxis));
    double C = (Math.Sin(rotation) * Math.Sin(rotation)) / (majorAxis * majorAxis) + (Math.Cos(rotation) * Math.Cos(rotation)) / (minorAxis * minorAxis);

    //计算椭圆方程增加平移(椭圆中心坐标,即向量(P,Q))后的一般式：Ax² + Bxy + Cy²−(2AP + BQ)x−(2CQ + BP)y + (AP²+ BPQ + CQ²−1)= 0
    double P = centerX;
    double Q = centerY;

    //关于X的二元一次方程：Ax² + (By-2AP-QB)x + Cy²-(2CQ + BP)y +  (AP²+ BPQ + CQ²−1)= 0
    //令δ=0，b²-4ac 则得到关于y公式：(B²-4AC)y²+[4A2CQ + 4ABP-2B(2AP+BQ)]y+(2AP+BQ)²-4A(AP²+ BPQ + CQ²−1) = 0;
    //求解y:

    double a = B * B - 4 * A * C;
    double b = 4 * A * 2 * C * Q + 4 * A * B * P - 2 * B * (2 * A * P + B * Q);
    double c = (2*A*P + B*Q) * (2*A*P + B*Q) - 4*A*(A*P*P + B*P*Q + C*Q*Q - 1);

    maxY = (-b + Math.Sqrt(b * b - 4 * a * c)) / (2 * a);
    minY = (-b - Math.Sqrt(b * b - 4 * a * c)) / (2 * a);

    if(maxY < minY)
    {
        double tempV = maxY;
        maxY = minY;
        minY = tempV;
    }

    //关于X的二元一次方程：Cy² + (Bx-2CQ-BP)y + Ax²-(2AP + BQ)x + (AP²+ BPQ + CQ²−1)= 0
    //令δ=0，b²-4ac 则得到关于y公式：(B²-4AC)x²+[4C(2AP+BQ)-2B(2CQ+BP)]x+(2CQ+BP)²-4C(AP²+ BPQ + CQ²−1) = 0;
    //求解x:
    a = B* B - 4*A*C;
    b = 4*C*(2*A*P + B*Q) - 2*B*(2*C*Q + B*P);
    c = (2 * C * Q + B * P) * (2 * C * Q + B * P) - 4 * C * (A * P * P + B * P * Q + C * Q * Q - 1);
    maxX = (-b + Math.Sqrt(b * b - 4 * a * c)) / (2 * a);
    minX = (-b - Math.Sqrt(b * b - 4 * a * c)) / (2 * a);
    if (maxX < minX)
    {
        double tempV = maxX;
        maxX = minX;
        minX = tempV;
    }
    return true;
}

参考：https://blog.csdn.net/fangmin723/article/details/118595271
参考：https://blog.csdn.net/liuxiang3/article/details/114258907