【指北】动态规划从入门到入坟

前言

本【指北】适合正在学习 DP 的 OIer。

本【指北】中不仅有简单内容，还有较难内容，总体来讲适合不同水准的选手。

本人才疏学浅，请大佬们在评论区中指出错误，我会加以改进与完善！

Part 0 DP 是啥

What is DP? What can DP do? What can't DP do?

动态规划（Dynamic Programming），简称 DP。

DP 能干嘛？我为啥不贪心？

• 基础的 DP 较为简单，且容易实现。
• DP 能够得到贪心获得不到的正确答案。
• DP 可扩展性强，你可以在大部分地方使用。（点名表扬某 AI, 打 CF 全写的是 DP）

这么说，DP 是万能的？不不不。

下面列出了 DP 的部分缺点：

• 复杂度较高，有些时候需要优化

• 手推柿子需要有一定数学基础

• 对新手不太友好

• 不太好理解

• 标准式用处不大，只能用于概念的理解

• 状态设计需要结合题目

不过，我们面对部分问题，仍有相应的解决方案。

话不多说，开始踏上我们的学习路程吧！

Part 1 线性 DP

线性 DP，顾名思义，就是给你一条直线，以直线上的点坐标为状态，答案从之前已决策过的点中转移过来。

下面给出线性 DP 的一般式（非标准，自己总结的）：

\[f_i = f_{i - a} + v \]

我们结合一道经典例题进行讲解：

以 P1095 守望者的逃离为例。题目链接传送门

在这道题里面，我们发现可以把时间套在 \(i\) 上，那么进行分类讨论（设 \(f(i)\) 为当时间为 \(i\) 时，策略是魔力能耗则耗，不能耗则恢复的最大的行走距离；而 \(M\) 为当时间为 \(i\) 时，能耗则耗，不能耗则恢复的魔力数目 ）：

① \(M \ge 10\)

显然，消耗魔力闪现比走路更快，能耗则耗，选择消耗魔力。

此时，\(f_i = f_{i - 1} + 60\)，\(M\) 减去 10。

② \(M < 10\)

显然，他耗不动，所以尝试停下来。

此时，\(f_i = f_{i - 1}\)，\(M\) 加上 4。

接下来，如果停下来回魔力的状态比不耗魔力走路的状态要慢，那选择不耗魔力走路。

为什么是对的呢？

显然，我每一个状态都有最优子结构，我每一个状态只从前面的最优的状态转移过来，自然是对的。

回顾一下内容。接下来提供几道例题：

摆花 甚至不需要分类讨论。

乌龟棋 暴力 DP。

Part 2 背包问题

背包问题，顾名思义，就是给你一坨没有价值有重量的物品，一個有容量的背包，让你把价值总计最大的那些物品扔进去。

那么，我们根据物品可取几个，将背包问题分为了 0/1 背包、多重背包和完全背包。

Part 2.1 0/1 背包

物品只能取一个或零个。

下面给出 0/1 背包的一般式（设 \(f_{i, j}\) 为考虑到第 \(i\) 个物品时，背包容量为 \(j\)）：

\[f_{i, j} = \max \begin{cases} f_{i - 1, j} \\ f_{i - 1, j - w_i} + v_i \\ \end{cases} \]

1. 不取

此时，相当于考虑到第 \(i - 1\) 个物品，而不消耗容量，即 \(f_{i, j} = f_{i - 1, j}\)

2. 取

此时，相当于考虑到第 \(i - 1\) 个物品，消耗 \(w_i\) 的容量，而获得 \(v_i\) 的价值，即 \(f_{i, j} = f_{i - 1, j - w_i} + v_i\)

Tips

有些题目的空间限制会把你卡没，所以考虑优化。

我们看到 \(f_i\) 只与 \(f_{i - 1}\) 有关系，所以将表示考虑到第 \(i\) 个物品的那一维去掉，即：

\[f_j = \max \begin{cases} f_j \\ f_{j - w_i} + v_i \\ \end{cases} \]

注意将体积 \(j\) 倒着遍历，否则会取到当前这一行的状态。

这个优化像是将数组滚动起来，因此被称为滚动数组优化。

Part 2.2 多重背包

物品可以取有限个。

下面给出多重背包的一般式（设 \(f_{i, j}\) 为考虑到第 \(i\) 个物品时，背包容量为 \(j\)，取 \(k\) 个物品）：

\[f_{i, j} = \max \begin{cases} f_{i - 1, j} \\ f_{i, j - k \cdot w_i} + k \cdot v_i \\ \end{cases} \]

方程容易理解，下面考虑优化。

我们学欧姆定律时，有没有想过电阻箱的几个电阻为什么不是二的 \(k\) 次方？

于是我们想到，把每个物体最多能取的个数进行二进制的拆分，将问题转换为 0/1 背包，将时间复杂度优化至 \(\mathcal{O}(M \sum_{i = 1}^N \log_2 w_i)\)，十分优秀。

Part 2.3 完全背包

物品可以无限取。

下面给出完全背包的一般式（设 \(f_{i, j}\) 为考虑到第 \(i\) 个物品时，背包容量为 \(j\)）：

\[f_{i, j} = \max \begin{cases} f_{i - 1, j} \\ f_{i, j - w_i} + v_i \\ \end{cases} \]

这是什么意思呢？就是要么不取，要么取。

这不跟 0/1 背包一毛一样吗... 等一下，第二项怎么改了？

是的，因为我可以仍在考虑这一物品时继续取，所以是 \(f_{i, j - w_i}\)。

跟 0/1 背包一样，完全背包也有优化，不过体积 \(j\) 是正着遍历的。

Part 3 区间 DP

顾名思义，以区间为状态进行转移，常用方程：

自两个区间合并而来的，枚举划分点 \(k\)（有时合并需要费用 \(w\)）。

\[f_{l, r} = f_{l, k} + f_{k + 1, r} + w \]

注意区间合并时为了保证状态已经计算过，循环中第一维是步长（区间长度）。

下面结合一道例题：Zuma

先设计状态，设 \(f_{l, r}\) 为消除区间 \([l, r]\) 的最小花费。

则易知：

\[\large f_{l, r} = \min_{k = l}^{r - 1} \begin{cases} f_{l, k} + f_{k + 1, r} \\ f_{l + 1, r - 1} \quad (arr_l = arr_r) \\ \end{cases} \]

就是说若两头相同，则可以转移自一个回文串（一个回文串首末加上同一个数还是回文串）。

否则枚举划分点，转移自两个区间之和。两者取最小值。

之后可以做做例题：涂色

Part 4 图上 DP

注：因为树形 DP 也算是图上 DP，所以不单独拎出来说了。

顾名思义，图上 DP 就是在一张图上做 DP。

本部分前置芝士：链式前向星、Tarjan 缩点、DFS。

对于每个节点，都进行 DP，那么常用方程如下（设 \(u\) 为当前节点，\(v\) 为可达的节点）：

\[f_u = \min\{f_v + w_{u \to v}\} \]

关于例题，树形 DP 与图上 DP 的题目多得过于泛滥，而且方程多样，不再赘述。

若想看本人的例题讲解，请移步至（都是有点思维量的题目，新手也可以先去写 选课、没有上司的舞会 和 二叉苹果树）：

P7238 迷失森林 题解 题目链接

P7846 Arcade hall / 街机厅 题解 题目链接

P1269 信号放大器 题解 题目链接

小问题：

当你发现有环怎么办？

可以使用 Tarjan 缩点，使得原图变成了 DAG，这样就没有环的问题了。

Part 5 数位 DP & 状压 DP

注：由于这两种 DP 思想有点像，故将它们放在一起。

Part 5.1 数位 DP

顾名思义，数位 DP 即在数字的每一位做 DP。

能用在哪里呢？计数类 DP 有可能是。

下面结合一道例题进行分析：P2657 windy 数

根据题意，要我们求出 \([a, b] (a < b)\) 内的 Windy 数的个数。

思索一下发现可以先求出 \([1, a]\) 与 \([1, b + 1]\) 内的 Windy 数，然后相减即为正确答案。

那么就可以设计 DP 方程辣。设 \(f_{i, j}\) 为考虑到第 \(i\) 位上一位的数为 \(j\) 的方案个数。

方程很好写：

\[f_{i, j} = \sum_{k = 0}^9 \begin{cases} 0 &\quad (|j - k| < 2) \\ f_{i - 1, k} &\quad (|j - k| \ge 2) \\ \end{cases} \]

不过求完之后还是得计算最终答案。设 \(ans_x\) 为 \([1, x]\) 区间内的 Windy 数，答案由三部分组成 （\(len_x\) 为 \(x\) 的位数，从高到低）：

1. 所有位数小于 \(len_x\) 的。
2. 位数为 \(len_x\) 但是最高位小于 \(x\) 的最高位的。
3. 位数为 \(len_x\) 而且最高位等于 \(x\) 的最高位的。从 \(len_x - 1\) 到 \(1\) 枚举每一位，先枚举可能的 \(j\) 转移累加，如果该位与上一位之差小于 \(2\) 就说明后面的数就已经处理过了，不必继续判断。

这样这题就做完啦。

Part 5.2 状压 DP

顾名思义就是把方程的状态压缩至可以储存。例题 P2704 [NOI2001] 炮兵阵地

看完题就应该会设计啦。我们将每一行每一个格子放不放炮兵的状态压成二进制数，这样就不会 MLE。

设 \(f_{i, s, ps}\) 表示考虑到第 \(i\) 行，该行状态为 \(s\)，上一行状态为 \(ps\) 的最大炮兵放置数目，则有（上一行状态为 \(pps\)，状态 \(s\) 的炮兵数目记为 \(sum_s\)）：

\[f_{i, s, ps} = \max \begin{cases} f_{i, s, ps} \\ f_{i - 1, ps, pps} + sum_s \quad (\text{需要满足条件}) \\ \end{cases} \]

那么问题来了，这个条件是什么？

首先要保证答案合法才能转移，因此涉及到的所有状态都不能有相邻的炮兵。

那么就分两种情况考虑：

1. 状态本身：右移一位，位与原状态；右移两位，位与原状态。有任意一个不为 \(0\) 的就不合法。注意不能在山丘上放炮兵...
2. 状态之间：本行状态与上一行状态位与，本行状态与上上行状态位与，上行状态与上上行状态位与。有任意一个不为 \(0\) 的就不合法。

那么这样就做完啦。不过结合前面学的滚动数组，你就不能优化一下吗？

发现我的方程中求一行只会用到前一行的答案，因此可以使用滚动数组优化空间。

下面推荐几道用到状压思想的题目：

P3869 宝藏 虽然不是 DP，但是也可以用来练习状压。

P1879 Corn Fields G 类似于炮兵阵地，思路清晰。

P1896 互不侵犯 长得挺像八皇后的哈哈。

P4011 孤岛营救问题 也不是 DP，但是是状压分层图经典好题。

Part 6. 轮廓线 / 插头 DP

是的，你没有听错！现在就在 10 min 之内教会你插头 DP。

轮廓线 DP，顾名思义就是在棋盘问题中，将当前决策格子作为已决策与未决策格子划分构造一条线，如图：

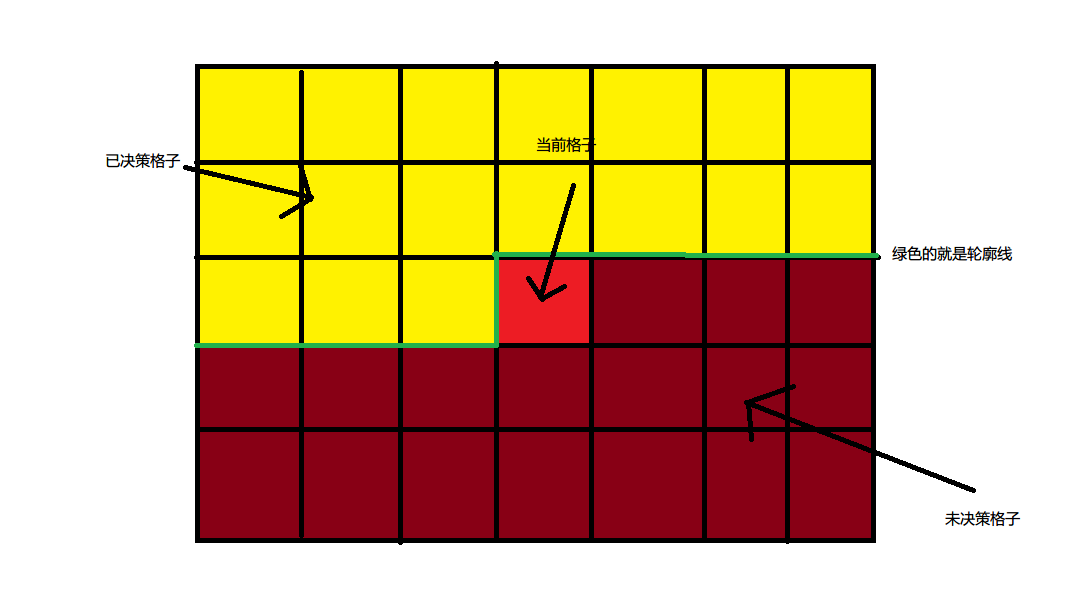
那么就以轮廓线为状态，去进行转移。这也用到了状压的思想。

插头 DP，顾名思义 就是将一个格子拆成四个插头：

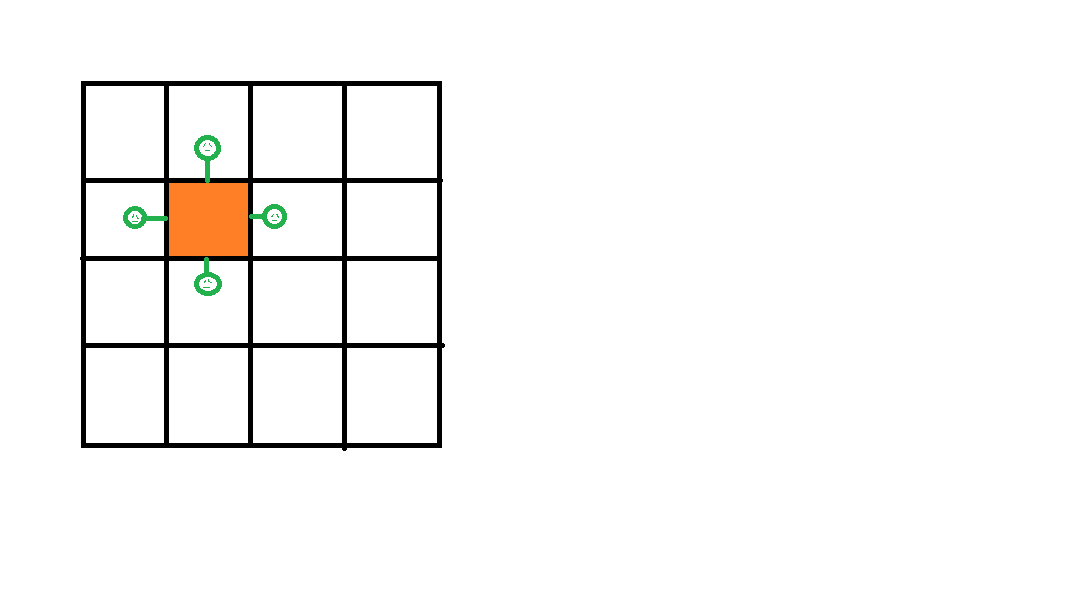
然后记录轮廓线上的插头状态，进行 DP。

为啥要定义插头？很简单，它规定了格子是否能够相连，而大部分棋盘问题格子都是可以相连的。这样我们可以根据轮廓线上的插头转移自所有合法状态。

下面来看 CDQ 大佬《基于连通性状态压缩的动态规划问题》中的例题：P5056 插头 DP

考虑将插头的相连性记录至状态，那就有了两种表示法：

1. 最小表示法

很简单，就是从左到右把联通的插头标为同一个编号。

2. 括号表示法

考虑到插头两两匹配的特性，可以联想到括号匹配。

定义轮廓线上的联通分量最左端的插头记为左括号，最右端的插头记为右括号，没有插头记为 \(0\):

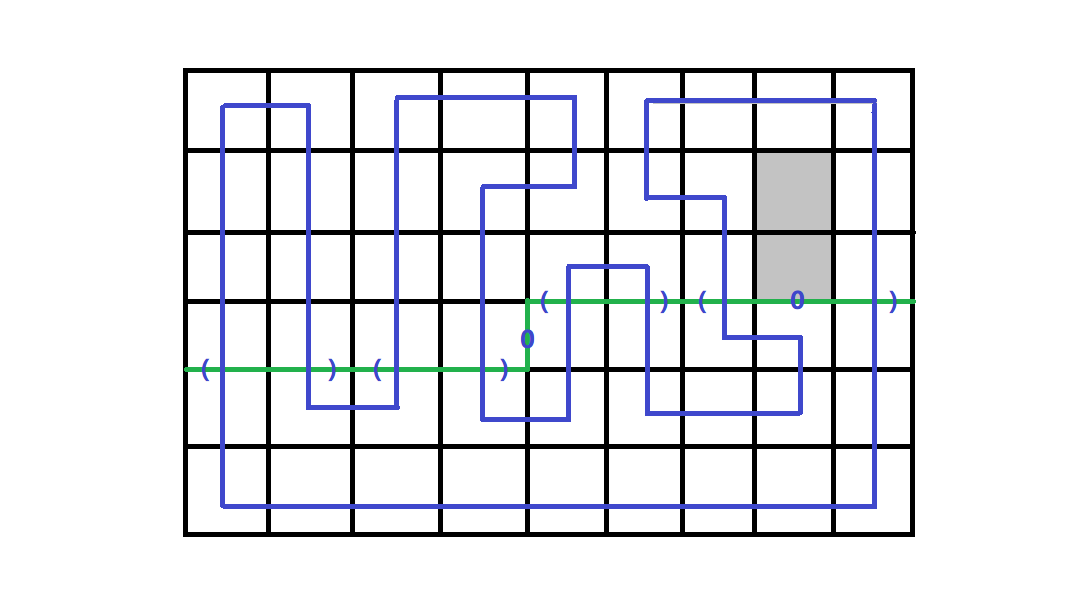
可以看到明显是个括号匹配。我们可以用三进制记录，不过为了方便使用四进制。

---

那么选好了表示法以后就可以快乐的分类讨论了。

1. 没有左、上插头

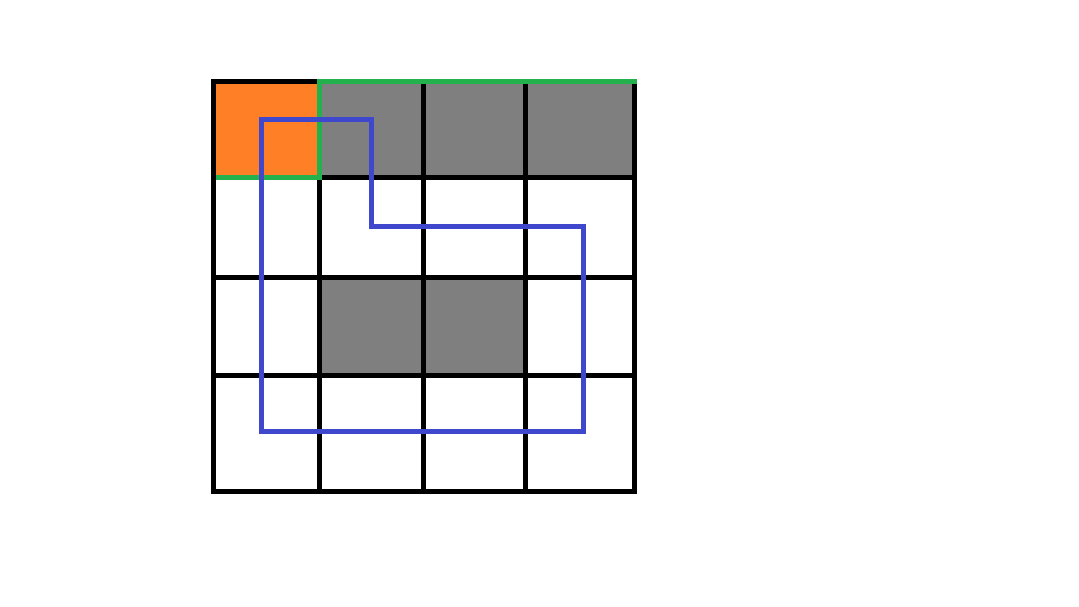
直接新建一个联通分量。往下面和右边造插头。

2. 两个插头都有

那就合并呗，否则造不出回路。

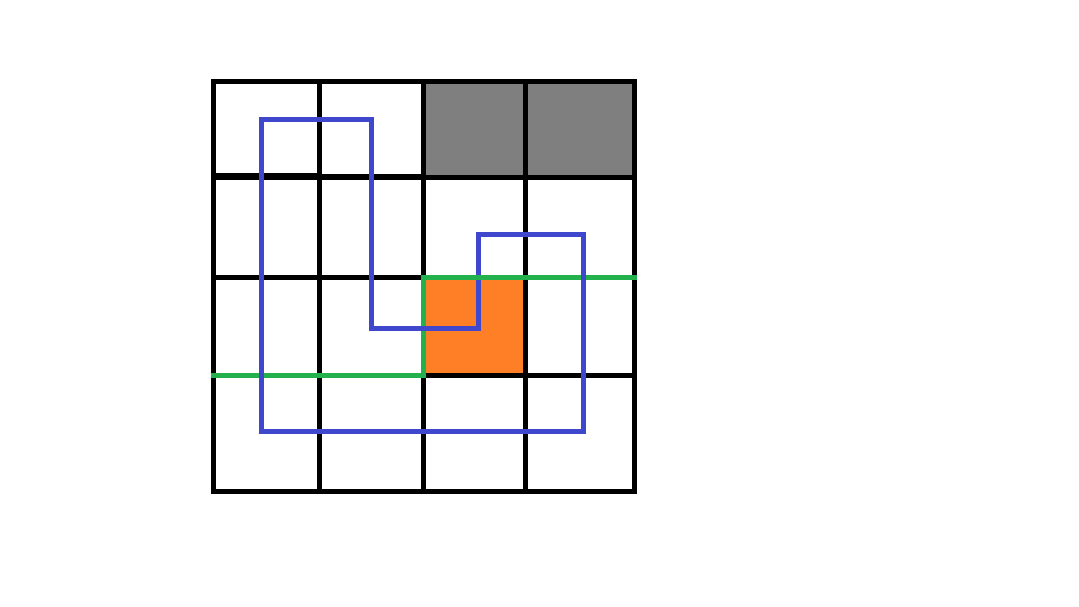
注意当这两个插头联通时，只有当这个格子为最后一个可以铺线的格子时才合法。

（因为只能产生一个环，既然你这一步都完成了整个环，那么后面的格子就无法成为环的一员了）

3. 只有一个插头

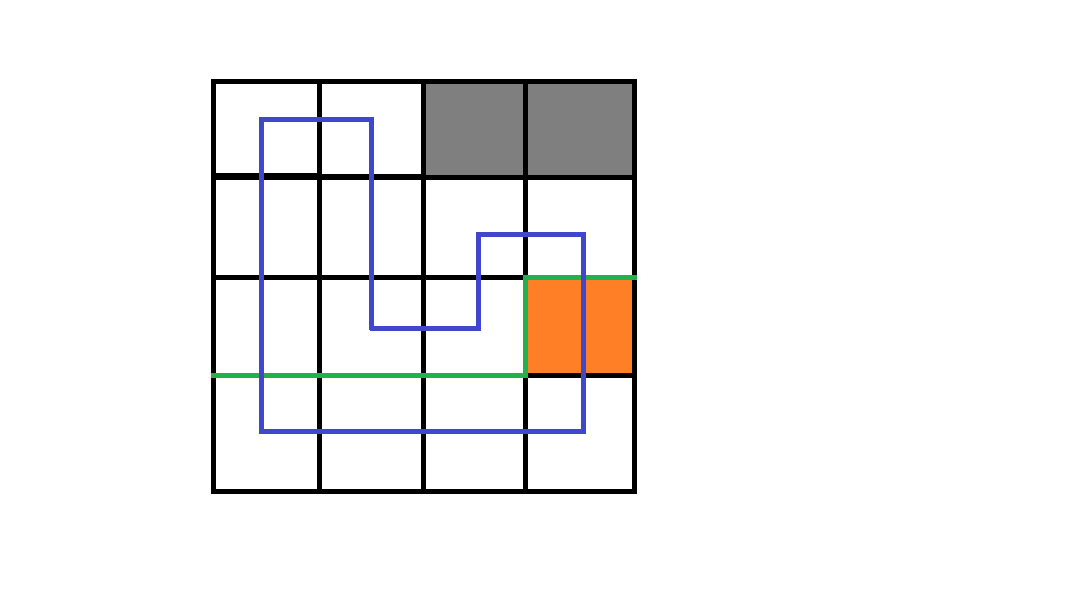
那就把线接过来，然后分成建右、下插头两种情况。

---

至此，分类讨论结束。题目就做完啦。

下面推荐几道插头 DP 练手题：

P5347 俄罗斯方块 千万不要做，太难了。

P6758 Vim 略微有点需要转化。

P4262 白金元首与莫斯科 骨牌覆盖问题。

P3272 地板 当年可是紫题啊... 思路简单，抓住 L 形特点即可。（不过还是凭着恶臭的分类讨论晋升到了黑题）

Part 7. 经典优化

没错我们终于来到了优化部分。

Part 7.1 单调队列优化

针对线性 DP 的方程，考虑维护其贡献单调性，进行单调队列优化。做法就是把有价值的保留，没意义的删掉。

例题：P1725 琪露诺

考虑枚举 \(i\)，枚举要跳的位置 \(j\)，复杂度为 \(\mathcal{O}(N (R - L + 1))\)，无法通过。

先列出方程吧：

\[f_i = \max_{i - L \le j \le i - R} \{f_{j} + A_i\} \]

然后就发现单调队列的用处了：可以让窗口大小为 \(R - L + 1\)，然后维护 \(f_i\)，每次都从最优者转移，再入队。

这样复杂度就下降了，成为了 \(\mathcal{O}(N)\) 的线扫。

Part 7.2 斜率优化

就是针对方程：

\[f_i = a_i \cdot b_j + c_i + d_j \]

的玄学优化。

例题：P3195 玩具装箱

先预处理前缀和 \(sum\)，然后写出柿子（令 \(A_i = sum_i + i, B_i = A_i + L + 1\)）：

\[\begin{aligned} f_i &= \min \{f_j + (sum_i - sum_j - L + i - j - 1)^2\} \\ &= \min \{f_j + (A_i - B_j)^2\} \\ &= \min \{f_j + A_i^2 - 2A_i B_j + B_j^2\} \\ \end{aligned} \]

假定 \(f_i = f_j + A_i^2 - 2A_i B_j + B_j^2\)，令 \(X = B_j, Y = f_j + B_j^2\)：

\[Y = f_i + 2A_i X - A_i^2 \]

这个就成了斜率为 \(2A_i\) 的直线。那么任务就是缩小截距。

发现题目中的好多玩意都具有单调性，考虑单调队列优化：

维护一个下凸壳，使得相邻两点之间的连线斜率单调上升。弹出对当前无意义的点（就是斜率小于 \(2A_i\) 的）获得当前最优，计算出 \(f_i\)，弹出在凸壳内部的点（截距肯定大），插入这个点。

那就做完啦。复杂度为 \(\mathcal{O}(N)\)。

Part 7.3 CDQ 分治

啊啊啊又是 CDQ 大佬。

简单来讲就是先求解左边的子问题 （后序遍历！！！），再处理左边的答案对于右边的答案的影响，再解决右边的子问题。

例题：P4027 货币兑换

先贴柿子：

\[x_i = f_i \frac{Rate_i}{A_i Rate_i + B_i}, y_i = f_i \frac{1}{A_i Rate_i + B_i}, f_i = \max \begin{cases} f_{i - 1} \\ \max \{ x_j A_i + y_j B_i\} \end{cases} \]

斜率乱搞：

\[\frac{y_j - y_k}{x_j - x_k} > - \frac{A_i}{B_i} \]

什么竟然没有单调性... 那么就要请出我们的 CDQ 分治了。

首先按照 \(- \frac{A_i}{B_i}\) 排序，左半边按照时间排序，确保用时间早的更新时间晚的。

再单调队列建立上凸壳转移，最后再按照 \(x\) 排个序即可。复杂度 \(\mathcal{O}(N \log_2^2 N)\)，勉强能过，尝试优化。

发现 CDQ 分治的壳子其实是个归并排序的壳子，那么再往里面添加归并排序即可。复杂度 \(\mathcal{O}(N \log_2 N)\)，可以通过。

Part 7.4 四边形不等式优化

对于区间 DP 的优化。

四边形不等式：

\[w_{a, b} + w_{c, d} \le w_{a, d} + w_{b, c} \quad (a \le b \le c \le d) \]

即交叉小于包含。那如何证明方程符合四边形不等式呢？

四边形不等式判定定理：

若对于任意 \(a < b\) 均有 \(w_{a, b} + w_{a + 1, b + 1} \le w_{a, b + 1} + w_{a + 1, b}\)，则 \(w_{a, b}\) 满足四边形不等式。

证明：

对于任意 \(a + 1 < c\) 都有 \(w_{a, c} + w_{a + 1, c + 1} \le w_{a, c + 1} + w_{a + 1, c}, w_{a + 1, c} + w_{a + 2, c + 1} \le w_{a + 1, c + 1} + w_{a + 2, c}\)。

可以推出来：

\[w_{a, c} + w_{a + 2, c + 1} \le w_{a, c + 1} + w_{a + 2, c} \]

于是可以推广至任意数。发现 \(b\) 亦是如此，证毕。

决策单调性：

满足四边形不等式一定满足决策单调性。证明：

设 \(pos_i\) 为 \(f_i\) 的决策点。要证明 \(pos_{i - 1} \le pos_i\), 先假设 \(pos_{i - 1} > pos_i\).

易得：

\[\begin{cases} f_{pos_i} + w_{pos_i, i} \le f_{pos_{i - 1}} + w_{pos_{i - 1}, i} \\ w_{pos_i, i - 1} + w_{pos_{i - 1}, i} \le w_{pos_i, i} + w_{pos_{i - 1}, i - 1} \end{cases} \]

。

综合可得：

\[f_{pos_i} + w_{pos_i, i - 1} \le f_{pos_{i - 1}} + w_{pos_i, i - 1} \]

这样就发现问题了，怎么 \(pos_i\) 变成 \(f_{i - 1}\) 的决策点了？因此假设不成立，原命题得证。

下面直接看例题：P4767 邮局

首先给坐标 \(x\) 排个序。然后手推方程：

\[f_{i, j} = \min \{f_{k, j - 1} + w_{k + 1, i}\} \]

其中 \(w_{k + 1, i}\) 表示在村庄 \(i, j\) 之间（含左右端点）的一个村庄放邮局的最小距离总和。可得放中间显然 \(w\) 可以预处理得来，于是我们写出递推式：

\[w_{i, j} = w_{i, j - 1} + x_j - x_{\lfloor \frac{i + j}{2}\rfloor} \]

然后将其变化可得：

\[w_{i, j + 1} - w_{i, j} = x_{j + 1} - x_{\lfloor \frac{i + j + 1}{2}\rfloor} \tag{1} \label{1} \]

以及：

\[w_{i + 1, j + 1} - w_{i + 1, j} = x_{j + 1} - x_{\lfloor \frac{i + j + 2}{2}\rfloor} \tag{2} \label{2} \]

\(\eqref{1} - \eqref{2}\) 得：

\[w_{i, j + 1} + w_{i + 1, j} - w_{i, j} - w_{i + 1, j + 1} = x_{\lfloor\frac{i + j + 2}{2}\rfloor} - x_{\lfloor\frac{i + j + 1}{2}\rfloor} \geq 0 \]

继续变形不等式：

\[\begin{aligned} w_{i, j + 1} + w_{i + 1, j} - w_{i, j} - w_{i + 1, j + 1} &\geq 0 \\ w_{i, j + 1} + w_{i + 1, j} &\geq w_{i, j} + w_{i + 1, j + 1} \\ w_{i, j} + w_{i + 1, j + 1} &\leq w_{i, j + 1} + w_{i + 1, j} \end{aligned} \]

发现符合一开始我们讲的判定定理，即 \(w\) 满足四边形不等式，同时 \(f\) 也满足。

可得 \(f_{i, j}\) 的决策点 \(pos_{i, j}\) 满足：

\[pos_{i, j - 1} \leq pos_{i, j} \leq pos_{i + 1, j} \]

于是直接从这个区间里找决策点就行。复杂度降至 \(\mathcal{O}(PV)\)，可以通过。

Part 7.5 WQS 二分

应用范围：恰好选 \(m\) 个的最优方案。

应用前提：设 \(g_i\) 为强制选 \(i\) 个物品的最优方案，那么把所有的 \((i, g_i)\) 画出后一定形成一个凸壳。

那么 WQS 二分就是一个能去掉这一限制的东东。

不妨求一下 \(g_m\)。先二分斜率，毕竟斜率对应的凸壳切点是惟一的（共线的除外），快速算出切点。

然后因为答案同样具有单调性，所以可以二分求解。考虑如何快速计算切点。

发现我们要的切点使得切线的截距最大，而 \(b = g_x - kx\)，于是截距的意义就变成了所有物品的价值减去 \(k\)，这样就不再有限制了。

下面来看例题：P6246 邮局 加强版。默认大家都会邮局了，下面讲解如何优化成 \(\log\) 级。

发现邮局建的越多越好，所以直接建 \(M\) 个，随便联想一下转换成恰好建 \(M\) 个。

然后直接可以上 WQS 二分啦！？突然发现方程不太符合 WQS 的思想？

易证方程的决策单调性，所以我们考虑将找决策点 \(pos\) 变为找决策点可以转移到的目标。那么就直接记录可以转移到的范围即可，使用单调队列维护（考虑某个点是否会选择转移自它）。

那么就真的可以上 WQS 二分辣！复杂度 \(\mathcal{O}(N \log_2 N \log \omega)\)，可以通过。

Part 7.6 线段树优化

就是拿线段树优化某些转移的过程。

例题：P8476 「GLR-R3」惊蛰

发现 Subtask #2 的值域奇小无比，于是设 \(f_{i, j}\) 为当 \(b_i = j\) 时的答案，属于 1D/2D 的 DP。

考虑做一个后缀最小值进行优化，复杂度为 \(\mathcal{O}(NV)\)，可以拿 15 pts。

又发现 \(\forall i,j \in [1, N], \text{s.t.} \ b_i = a_j\)，因为如果不等于，一定比将 \(b_i\) 缩小为 \(a_j\) 的答案劣。（省去一个 \(C\) 能不优吗）

修改一下方程，设 \(f_{i, j}\) 表示 \(b_i\) 为 \(a\) 中第 \(i\) 大的数字，可以达到 \(\mathcal{O}(N^3)\), 稍微一想就可以发现做一个前缀最小值就可以优化掉一维。可以拿下 Subtask #1 的 25pts。

然后考虑优化啦。发现值域路线难以再次优化，考虑将 Subtask #1 的做法再次优化成 \(\log_2\) 级。

发现方程只转移自上一个人，考虑扔到线段树上去维护，计算每一个人的加入对答案的贡献。分类讨论：

\[f_{i, j} = \min \begin{cases} f_{i - 1, j} + b_j - a_i \quad &(1 \le j \le k) \\ f_{i - 1, j} + C \quad &(k + 1 \le j \le N) \\ \end{cases} \]

对于第二种情况可以简单的区间加。而对于第一种情况，一部分是 \(a_i\) 容易维护，而 \(b_j\) 不知道是谁，所以不好做。

发现两个序列都单调不增，所以相加后同样单调不增，区间最小值的位置仍不变。所以 \(b_j\) 就是右端点。

不过发现 \(f\) 为两个单调不增序列相接组成，不满足性质，于是最后再拿左边的右端点值拿来推平右区间即可。

复杂度约为 \(\mathcal{O}(N \log_2 N)\)。可以通过。

Part 7.7 矩阵乘法加速优化

前置知识：矩阵乘法。这个优化对于一些递推题很实用。但是写出柿子有些困难。

例题：P4910 帕秋莉的手环

计数类问题，考虑 DP。设 \(f_i\) 为放到 \(i\) 的方案, \(f_{i, 1}\) 表示放木，\(f_{i, 2}\) 表示放金，然后容易推出转移方程：

\[\begin{cases} f_{i, 1} = f_{i - 1, 2} \\ f_{i, 2} = f_{i - 1, 1} + f_{i - 1, 2} \end{cases} \]

但这个算法是 \(\mathcal{O}(TN)\) 的，不可能过的了。考虑优化。

由于我们知道矩阵快速幂能够优化递推，所以采用矩阵快速幂优化本题。

很轻松（真的吗）就能推出矩阵：

\[\begin{aligned} \left[ \begin{matrix} f_{i - 1, 1}, f_{i - 1, 2} \end{matrix} \right] \times \left[ \begin{matrix} 0, 1 \\ 1, 1 \end{matrix} \right] &= \left[ \begin{matrix} f_{i - 1, 1} \times 0 + f_{i - 1, 2} \times 1, f_{i - 1, 1} \times 1 + f_{i - 1, 2} \times 1 \end{matrix} \right] \\ &= \left[ \begin{matrix} f_{i, 1}, f_{i, 2} \end{matrix} \right] \end{aligned} \]

复杂度 \(\mathcal{O}(T \log_2 N)\), 可以勉强通过。

Part 8. 一些杂类 DP

一些你考场上大概碰不到的 DP。

Part 8.1 概率 DP

一种蛮有意思的 DP，考察了选手对于概率论的理解。

概率论初步：P2791 幼儿园篮球题

例题：POJ2096 Collecting Bugs

题面意思：

一个软件有 \(s\) 个子系统，会产生 \(n\) 种 bug。某人一天发现一个 bug，这个 bug 属于某种 bug 分类，也属于某个子系统。
每个 bug 属于某个子系统的概率是 \(\dfrac{1}{s}\)，属于某种 bug 分类的概率是 \(\dfrac{1}{n}\)。求发现 \(n\) 种 bug，且 \(s\) 个子系统都找到 bug 的期望天数。

设 \(f_{i, j}\) 为找到 \(i\) 种 bug 分类，\(j\) 个子系统时达到目标状态的期望天数。易得 \(f_{n, s} = 0\)。

于是考虑 \(f_{i, j}\) 转移自谁：

• \(f_{i, j}\)。即这个 bug 还是属于之前找到的子系统和 bug 类型。概率为 \(\dfrac{i \times j}{n \times s}\)。

• \(f_{i + 1, j}\)。即这个 bug 还是属于之前找到的子系统。概率为 \(\left(1 - \dfrac{i}{n}\right) \times \dfrac{j}{s}\)。

• \(f_{i, j + 1}\)。即这个 bug 还是属于之前找到的 bug 类型。概率为 \(\left(1 - \dfrac{j}{s}\right) \times \dfrac{i}{n}\)。

• \(f_{i, j + 1}\)。即这个 bug 是全新的。概率为 \(\left(1 - \dfrac{j}{s}\right) \times \left(1 - \dfrac{i}{n}\right)\)。

这样子就可以用 DP 求解了。

Part 8.2 SOS DP

即子集和 DP。它可以解决子集求和类问题。例题：CF1829H Don't Blame Me

这道题看起来跟求和没有关系，我们先考虑最 naive 的做法 \(\mathcal{O}(3^K)\) 的枚举子集，但是会超时。接下来介绍如何搞成 \(\mathcal{O}(K \cdot 2^K)\) 级别。

我们用集合来表示二进制数。设 \(S_i\) 为包含了 \(i\) 的二进制所有 \(1\) 的位置的一个集合。

若 \(S_i \cap S_j = S_i\)，即 \(S_i \in S_j\)，则其实际含义为 i & j = i。

然后我们要计算 \(S_i\) 的子集个数 \(A_i\)，这个就需要使用 SOS DP 进行求解，其本质是个状压。

转移代码：

for (int j = 0; j < k; ++ j)
	for (int i = 0; i < 1 << k; ++ i)
		if (!(i & (1 << j)))
			a[i] += a[i ^ (1 << j)];

这离答案还差一点。我们要计算任意匹配个数 \(f_i\)，因此快速幂计算 \(2^{a_i}\)，但显然有重复的。

因此我们要容斥一下。把子集的答案计数全部删去一遍（因为任意匹配已经算过）。最后答案为 \(\displaystyle\sum_{\operatorname{popcnt}_i = 1} f_i\)，别忘记若 \(N = K\) 时要减一（因为是全集，所以空集也会算一次）。

Part 8.3 动态 DP

这人有病吧讲这个。 典题：P4719 【模板】"动态 DP"&动态树分治

这题就是个求动态带点权最大权独立集的权。所以先做不带修版本。

设 \(f_{i}\) 为以 \(i\) 为根的最大权独立集的权，容易写出（分 \(i\) 取不取）：

\[\begin{cases} f_{i, 0} = \sum_{j \in son_i}{\max\{f_{j, 0}, f_{j, 1}\}}\\ f_{i, 1} = val_i + \sum_{j \in son_i}{f_{j, 0}} \end{cases} \]

接下来加上修改操作。因为点带权，且树上的转移点修改后只影响该点到根的这一条链上的答案，所以直接树剖。

我们用 \(g_{i, 0}\) 来表示 \(i\) 的所有轻儿子任意取的最大权独立集的权和，用 \(g_{i, 1}\) 来表示 \(i\) 的所有轻儿子都只取自己的最大权独立集的权和。写出方程（\(hson_i\) 表示 \(i\) 的重儿子）：

\[\begin{cases} f_{i, 0} = g_{i, 0} + \max\{f_{hson_i, 0}, f_{hson_i, 1}\}\\ f_{i, 1} = g_{i, 1} + f_{hson_i, 0} \end{cases} \]

这个一半可以矩乘优化，另外一半有个最大值所以无法优化。这时候定义广义矩乘：

\[C_{i, j} = \max_{k = 1}^N\{A_{i, k} + B_{k, j}\} \]

显然其满足结合律（因为涉及的操作全符合结合律），于是可以使用矩乘加速。

我们构造矩阵：

\[\left[ \begin{matrix} g_{i, 0}, &g_{i, 0} \\ g_{i, 1}, &-\infty \end{matrix} \right] \times \left[ \begin{matrix} f_{hson, 0} \\ f_{hson, 1} \end{matrix} \right] = \left[ \begin{matrix} f_{i, 0} \\ f_{i, 1} \end{matrix} \right] \]

然后用线段树维护链上的 \(g\) 矩乘乘积之类的，查询只需求根节点的整条重链的乘积。

注：2022 年 S 组考了这个，因此想要特地讲讲。

后言

历时半年，终于写完了这篇博客。这里感谢所有题目的贡献者。

部分资料来源于 动态规划部分简介 - OI Wiki (oi-wiki.org)。