图算法之——dijkstra算法

一.算法特点

目标：找出加权图中前往X的最短路径

适用于：无环有向加权图，且各边的权值为正

二.算法思路

 

三.算法示例演示

如下图，请找出结点v1到其他各个结点的最短路径：

 

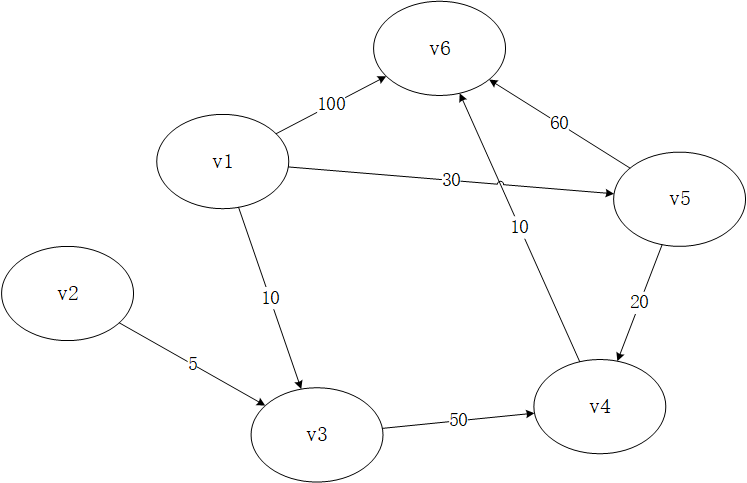
首先创建一个字典（散列表），该字典的键表示结点名字，值表示从v1到该结点的最短路径。下图中，字典初始化后只有v1的邻居节点被写入值：

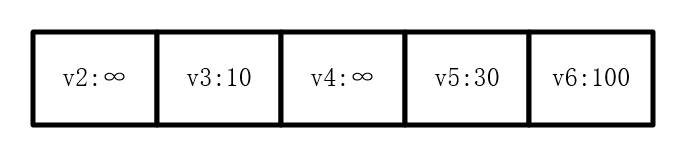
按照算法的思路，我们先找到距离起点最近的结点（v3），结点v3已经是最短路径了（因为迪杰特斯拉算法处理的是边权值为正的图，所以经其他任何节点再到v3的路径和不会小于v1到v3的权值，之后的步骤同理）。接着寻找v3的邻居节点（v4），更新v4的开销为10+50=60。此外，要完成这个需求，还应该定义一个字典，保存结点的父节点信息。此处将v4的父节点标为v3，并且把v3标记为处理过的结点。

 

接着再找到下一个距离v1最近并且没有被标记过的结点，重复以上步骤，v5的邻居节点有v4和v6两个，经过v5到达v4和v6的路径分别为50和90，将字典中对应的值修改后，将v4和v6的父节点改为v5（此处若经过v5的值大于原来的值则不应该修改父节点），标记v5为已处理结点。

   

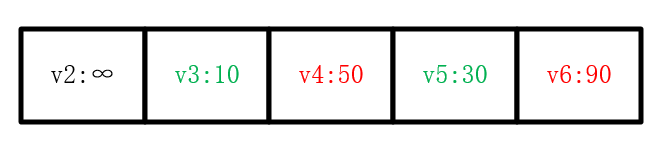
继续按照循环的思路，最后字典被修改为：

 

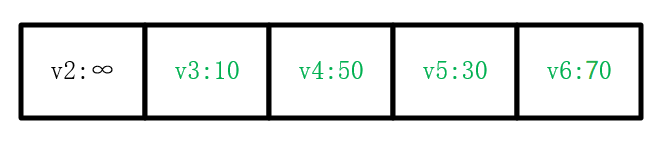
到目前，只有v2结点没有被处理过了。然而此时应当理解∞的含义，即没有任何一个结点可以到达v2结点，因此v2结点是不可到达的，没有最近距离。通过上述字典和记录父节点的列表即可求出最短距离及最短路径。

四.算法实现（Python）