数组与链表
简单记录下数据结构中最常用的两种线性数据结构:数组与链表。
数组
数组是一种最常见的链式结构,存储在一段连续的内存空间中,如下所示:
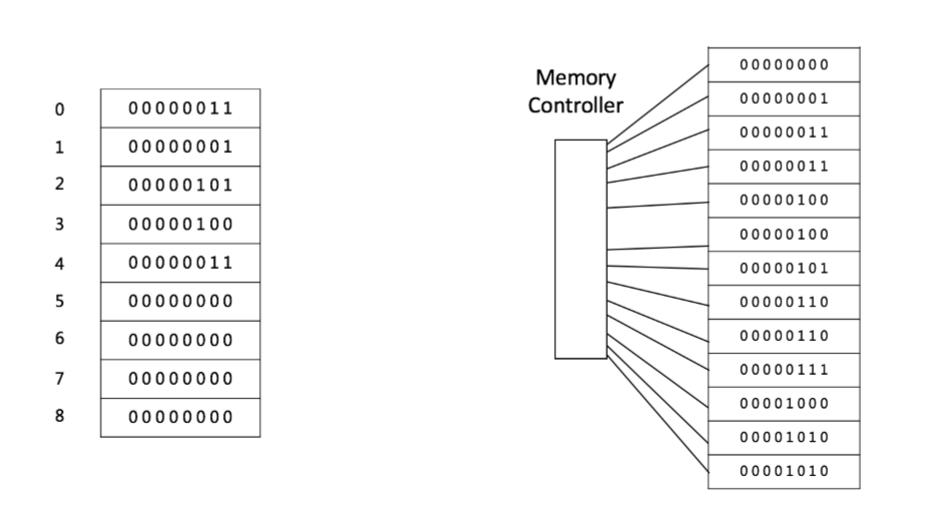
插入和删除操作:

根据这种结构,在数组中进行一些常规操作时的时间复杂度为:
- 插入: 平均O(n)
- 删除: 平均O(n)
- 查找(按索引): O(1)
- 查找(按值): 无序O(n) 有序O(log n)
说明:数组的插入操作中,最好情况是O(1)的,即直接加到数组最后。最坏情况是插入到数组开头,这就需要将后面的元素全部往后移动(我们需要尽量避免这种操作)。此外,插入操作可能还会引起数组的扩容操作。因此,插入操作平均的时间复杂度认为是O(n)。删除同理。
相关练习:

""" 给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。 示例: 输入: [0,1,0,3,12] 输出: [1,3,12,0,0] 说明: 必须在原数组上操作,不能拷贝额外的数组。 尽量减少操作次数。 """ """ ---------------------------------------------------------------------------------------------------------- 对于列表而言,插入和删除操作的时间代价是要高于查找及修改操作的。 所以在本题中,更高效的做法是:把数组中所有的非零元素,按顺序给数组的前段元素位赋值,剩下的全部直接赋值 0。 ---------------------------------------------------------------------------------------------------------- """ class Solution: def moveZeroes(self, nums): """ :type nums: List[int] :rtype: void Do not return anything, modify nums in-place instead. """ count = nums.count(0) index = 0 for i in nums: if i != 0: nums[index] = i index += 1 nums[-1: -count-1: -1] = [0 for i in range(count)] num = [0,1,0,3,12] res = Solution() res.moveZeroes(num) print(num)

""" 给定一个数组 nums 和一个值 val,你需要原地移除所有数值等于 val 的元素,返回移除后数组的新长度。 不要使用额外的数组空间,你必须在原地修改输入数组并在使用 O(1) 额外空间的条件下完成。 元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。 示例 1: 给定 nums = [3,2,2,3], val = 3, 函数应该返回新的长度 2, 并且 nums 中的前两个元素均为 2。 你不需要考虑数组中超出新长度后面的元素。 示例 2: 给定 nums = [0,1,2,2,3,0,4,2], val = 2, 函数应该返回新的长度 5, 并且 nums 中的前五个元素为 0, 1, 3, 0, 4。 注意这五个元素可为任意顺序。 你不需要考虑数组中超出新长度后面的元素。 说明: 为什么返回数值是整数,但输出的答案是数组呢? 请注意,输入数组是以“引用”方式传递的,这意味着在函数里修改输入数组对于调用者是可见的。 你可以想象内部操作如下: // nums 是以“引用”方式传递的。也就是说,不对实参作任何拷贝 int len = removeElement(nums, val); // 在函数里修改输入数组对于调用者是可见的。 // 根据你的函数返回的长度, 它会打印出数组中该长度范围内的所有元素。 for (int i = 0; i < len; i++) { print(nums[i]); } """ """ ------------------------------------------- 同01题,尽可能不在列表中进行增删操作 ------------------------------------------- """ class Solution: def removeElement(self, nums, val): """ :type nums: List[int] :type val: int :rtype: int """ length = len(nums) count = 0 for i in nums: if i != val: nums[count] = i count += 1 else: length -= 1 return length

""" 给定一个排序数组,你需要在原地删除重复出现的元素,使得每个元素只出现一次,返回移除后数组的新长度。 不要使用额外的数组空间,你必须在原地修改输入数组并在使用 O(1) 额外空间的条件下完成。 示例 1: 给定数组 nums = [1,1,2], 函数应该返回新的长度 2, 并且原数组 nums 的前两个元素被修改为 1, 2。 你不需要考虑数组中超出新长度后面的元素。 示例 2: 给定 nums = [0,0,1,1,1,2,2,3,3,4], 函数应该返回新的长度 5, 并且原数组 nums 的前五个元素被修改为 0, 1, 2, 3, 4。 你不需要考虑数组中超出新长度后面的元素。 说明: 为什么返回数值是整数,但输出的答案是数组呢? 请注意,输入数组是以“引用”方式传递的,这意味着在函数里修改输入数组对于调用者是可见的。 你可以想象内部操作如下: // nums 是以“引用”方式传递的。也就是说,不对实参做任何拷贝 int len = removeDuplicates(nums); // 在函数里修改输入数组对于调用者是可见的。 // 根据你的函数返回的长度, 它会打印出数组中该长度范围内的所有元素。 for (int i = 0; i < len; i++) { print(nums[i]); } """ class Solution: def removeDuplicates(self, nums): """ :type nums: List[int] :rtype: int """ length = len(nums) if nums: last_num = nums[0] index = 1 for i in nums: if i != last_num: nums[index] = i index += 1 last_num = i else: length -= 1 return length+1 # 循环第一次时last_num = nums[0],会认为重复,多减了一次 else: return 0 num = [] res = Solution() n = res.removeDuplicates(num) print(num, n)
链表
链表是一种元素内存空间离散排列的线性数据结构,如下图所示:
单向链表:
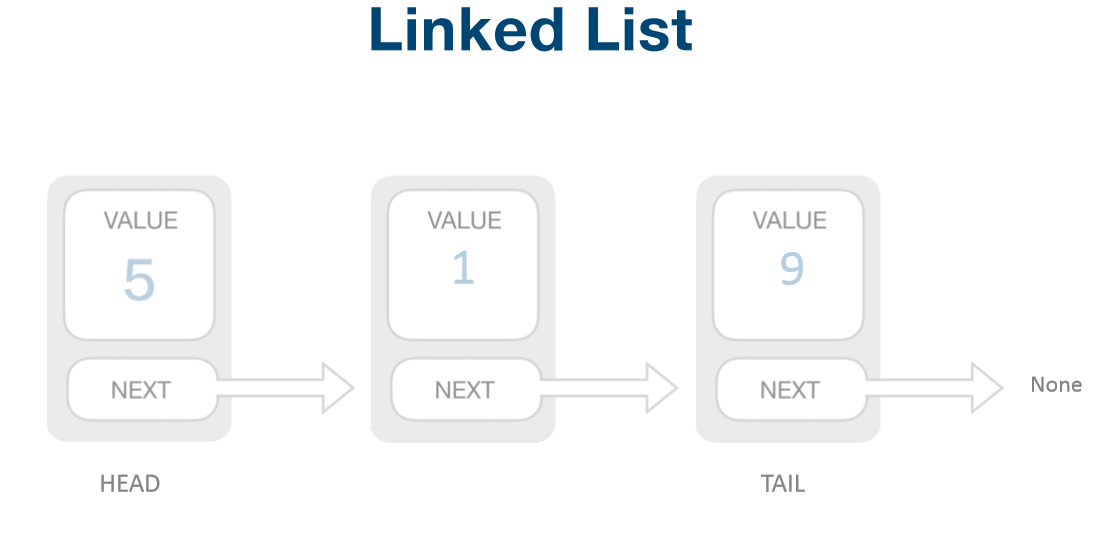
双向链表:
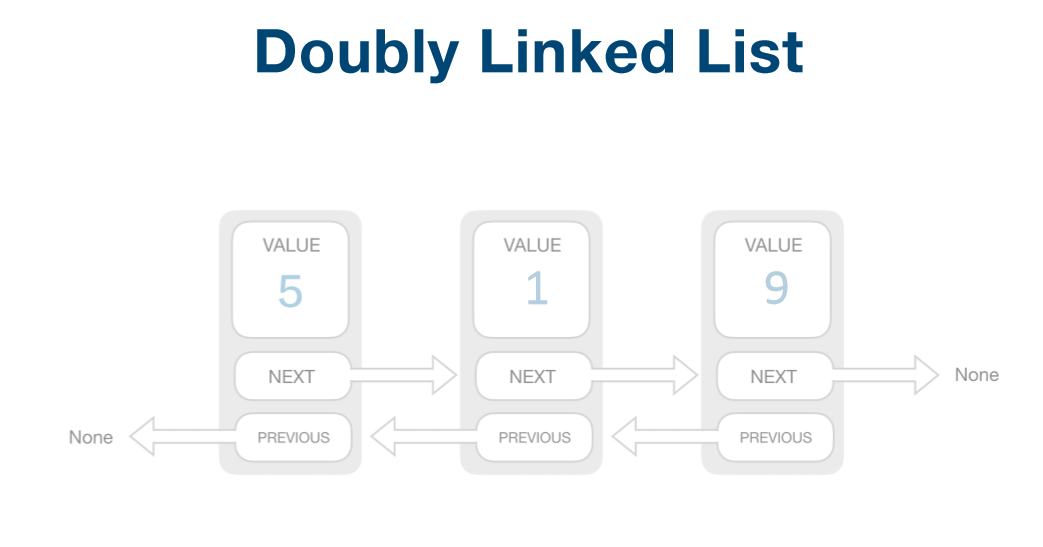
特点:
n个节点离散分配
每个节点只有一个前驱节点,每个节点只有一个后续节点
彼此通过指针相连(单项链表中只有指向后续节点的指针next,双向链表还有一个指向前驱结点的指针previous)
首节点没有前驱节点,尾节点没有后续节点
插入:

删除:
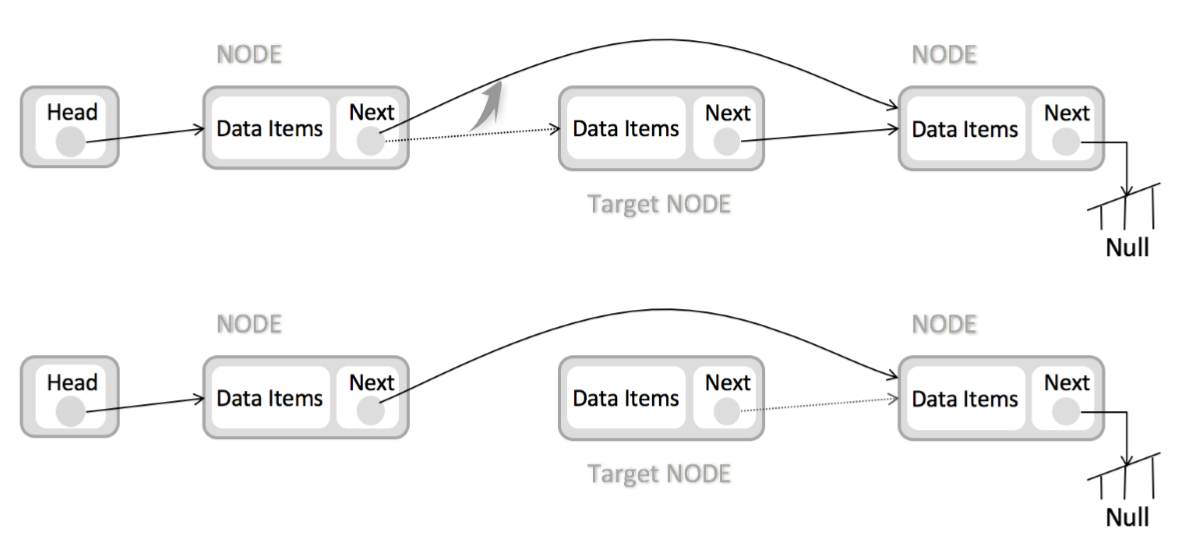
根据这种结构,在数组中进行一些常规操作时的时间复杂度为:
- 插入: O(1)
- 删除: O(1)
- 查找: O(n)
说明:尽管链表的插入和删除两种操作本身的时间复杂度为O(1),但是需要先查找到对应的节点才能进行相应的操作,因此在平时项目里我们很难会实际使用链表。但是有一种情况,比如区块链或者比特币,我们很少随机访问中间位置的节点,而绝大部分时候我们就在尾部叠加新节点。此外,虽然同为O(n)操作,链表查找第N个节点的时间再插入,比插入一个节点到数组,数组移动N个节点时间相比,数组移动节点的时间还是要多。
相关练习:

""" 反转一个单链表。 示例: 输入: 1->2->3->4->5->NULL 输出: 5->4->3->2->1->NULL """ # Definition for singly-linked list. class ListNode: def __init__(self, x): self.val = x self.next = None def reverseList(head): """ :type head: ListNode :rtype: ListNode """ cur, prev = head, None while cur: # cur, cur.next, prev = cur.next, prev, cur # 这里有一个关于python的坑 cur.next, prev, cur = prev, cur, cur.next return prev a = ListNode(1) b = ListNode(2) c = ListNode(3) d = ListNode(4) e = ListNode(5) a.next = b b.next = c c.next = d d.next = e e.next = None new_a = reverseList(a)

""" 反转链表在逻辑理解上并没有什么难度,遍历链表中的每个节点,将指向后继节点的指针指向它的前驱结点,第一个结点的后继结点指向空即可。在python实现中的我,却遇到了一个巨大的坑: 仔细观察上面循环中的两段代码,被注释的代码与下面的代码赋值的操作一模一样,唯一的区别仅仅是变量赋值的顺序不一样,对python语言有一定基础的朋友也许和我一开始想的一样,解释器会帮助我们算好等号右边的所有值,然后一次性赋给左边,这是python中独特的语法糖,不同于其他语言。(举一个简单的例子:交换a,b的值,只需要a,b=b,a一句话即可实现,原理是python解释器在底层会先生成一个(b,a)的元组,然后再分别将a,b引用到元组中b,a的内存地址,完成交换。而对于其他语言,我们需要自己再添加一个临时变量c,借助临时变量分步完成值的交换) 正是由于python语言的这种独特性质,让我深深的相信这两句代码的执行效果肯定是一模一样的,然而事实证明自己还是太年轻: 使用第一句代码执行,得到的结果是AttributeError: 'NoneType' object has no attribute 'next',而使用第二句代码去执行同样的操作,完美的得到了最终的结果!那么问题究竟出在了哪里?难道是我吃糖的姿势不对?下面,我从代码入手,来分析下这个问题: 首先,将头结点(a对象)的指针head传入函数,当前节点(cur)的值指向head,它的前驱结点(prev)是空值,进入循环,先从赋值语句的右边来看,cur.next, prev, cur此时的值分别为b的内存地址,None和a对象,将这三个值再分别赋给cur, cur.next, prev,执行cur = b的内存地址时,将cur变量指到b的内存地址。接下来为cur.next赋值为空,问题的关键出现了!按照之前的思路,我认为这里执行的操作是a.next = None,即让反转后a的后继结点为空。然而实际情况不是这样的,在python中对变量的赋值采用的是对内存地址的引用(理解这一句话很关键,在python中很多坑都和它有关,如函数的默认参数陷阱、深浅拷贝等问题),那么,在刚才执行cur = b的内存地址时,cur已经是b的地址了,cur.next = None这一语句实际上是将b对象的next属性设置为空,在下一次循环里,当代码先计算赋值语句右边的值,cur.next, prev, cur此时分别为变为None(不是c结点的地址了),a的地址,b的地址。然后继续给左边的cur, cur.next, prev赋值,cur = None,cur.next变为None.next,报错: 'NoneType' object has no attribute 'next',实际上这种写法的思路是没有问题的,但是因为python的这种引用赋值的特性,需要将我们代码中变量赋值的顺序略作修改,使cur的后继结点先反转到前驱结点后再更改cur的内存地址即可。 """ """ 总结: 1.python中的赋值语句是通过变量引用到值对应的内存地址,是一种引用赋值。 2.python中多变量赋值时,虽然是对所有变量一次性赋值,但并不代表这种赋值是同时发生的,还是按照先后顺序执行。 3.结合以上两点,发生了这次报错。这无关算法思路,而是对python语言的语法机制了解的还不够深入,解决问题的过程就是对已掌握知识点的复现和对自己知识盲区的查缺补漏,完善整体的知识脉络。 4.前路漫漫,还需努力。 """



