排序
排序算法研究的若干问题
- 排序成本模型:在研究算法的时候我们会计算比较和交换的次数,对于不交换元素的算法我们会计算数组访问的次数。
-
额外内存使用
排序算法的额外内存开销与运行时间是同等重要的,排序算法那可以分为两种,一是除了算法函数本身调用栈和固定数目的实例变量之外无需额外内存的原地排序算法,以及需要额外内存空间来存储一组数组副本的其他排序算法。
一、选择排序
算法思想:这是一种最简单的排序思想,先找出数组中的最小元素和数组第一个元素交换,然后从数组的第二个元素开始找出余下的元素中最小的那个跟数组的第二个元素进行交换,以此类推直到将整个数组排序。这种算法那叫做选择排序。因为他在不断的选择数组中最小的元素。
实现如下:
1 public static void sort(Comparable[] paramArray) {
2 for (int i=0; i<paramArray.length; i++) {
3
4 //find the minimum element from the rest of the Array
5 int minElement = i;
6 Comparable temp = paramArray[i];
7 for (int k=i+1; k<paramArray.length; k++) {
8 if (less(paramArray[k], temp)) {
9 temp = paramArray[k];
10 minElement = k;
11 }
12 }
13
14 //exchange
15 Comparable temp2 = paramArray[i];
16 paramArray[i] = paramArray[minElement];
17 paramArray[minElement] = temp2;
18 }
19 }
20

二、插入排序
就像我们平时玩扑克牌一样,在抓牌的时候,手里的牌总是已经排好序的,抓下一张牌的时候,会把它插入到正确的位置。为了给要插入的元素腾出位置,我们需要将后面的所有元素都向后移动一个位置。插入排序所需的时间取决于初始数组元素的顺序。
1 public static void insertionSort(Comparable[] paramArray) {
2 for(int i=1; i<paramArray.length; i++) {
3 for (int j=0; j<=i; j++) {
4 if (less(paramArray[j], paramArray[i])) {
5 continue;
6 }
7
8 //将要插入位置以后的数组元素向后移动一个元素
9 Comparable insertElement = paramArray[i]; //要插入的元素
10 for (int k=i; k>j; k--) {
11 paramArray[k] = paramArray[k-1];
12 }
13
14 paramArray[j] = insertElement; //元素插入
15 }
16 }
17 }
18
19 private static boolean less(Comparable comparable, Comparable temp) {
20 return comparable.compareTo(temp)<0 ? true : false;
21 }
三、希尔排序
四、归并排序
将两个有序数组合并成一个有序数组,这就是归并排序算法的核心思想。要将一个数组排序,可以先将其分成两个数组(递归的),对这两个小数组分别排序,最后再将两个有序数组合并。归并排序吸引人的地方在于它的时间复杂度是o(NlgN),缺点它并不一个原地排序算法,需要的额外空间和输入规模N成正比。
-
归并算法
归并排序的核心算法就是归并的实现。下面是一种原地归并的抽象方法。即将原来部分有序的数组归并有序化。
1 /**********************************************************************************
2 * 将一个部分有序的数组(low到mid有序,mid到high有序),归并成一个有序的数组
3 * 先将原数组复制到另一个辅助数组中,然后对这两个数组分别遍历,每次选取最小的一个元素放入
4 * 到原来的数组中
5 * *******************************************************************************/
6 private static void merge (Comparable[] paramArray, int low, int mid, int high ) {
7 //将原数组中的元素复制大辅助数组中
8 Comparable[] auxiliaryArray = new Comparable[paramArray.length];
9 for (int i=low; i<=high; i++) {
10 auxiliaryArray[i] = paramArray[i];
11 }
12
13 //将两个有序数组归并到原来的数组中
14 int lowLocation = low;
15 int midLocation = mid + 1;
16
17 for (int j=low; j<=high; j++) { //归并并回到paramArray[low....hign]
18 if (lowLocation > mid) {
19 paramArray[j] = auxiliaryArray[midLocation];
20 midLocation ++;
21 }
22 else if (midLocation > high) {
23 paramArray[j] = auxiliaryArray[lowLocation];
24 lowLocation ++;
25 }
26 else if (less(auxiliaryArray[lowLocation], auxiliaryArray[midLocation])) {
27 paramArray[j] = auxiliaryArray[lowLocation];
28 lowLocation ++;
29 }
30 else if (less(auxiliaryArray[midLocation], auxiliaryArray[lowLocation])) {
31 paramArray[j] = auxiliaryArray[midLocation];
32 midLocation ++;
33 }
34
-
自顶向下的归并排序
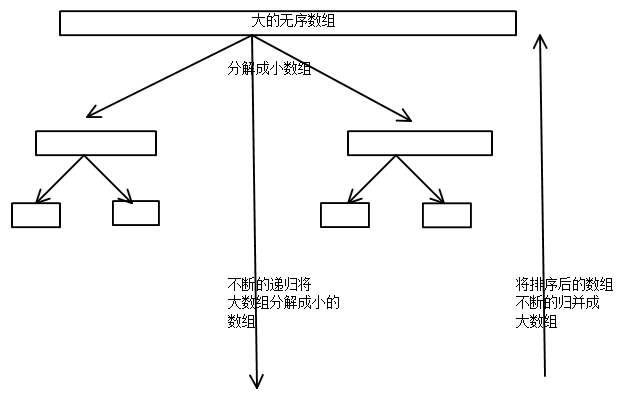
我们已经实现了上述的归并算法,那么我们可以用分治法的思想对一个数组进行归并排序。我们要对一个大的数组进行排序,可以先将这个数组分成两部分分别排序,然后对这两部分已经排序好的数组进行归并,同样的对于划分的两个小数组同样可以用上述的思想去排序。
1 public static void mergeSort(Comparable[] paramArray) {
2 mergeSort(paramArray, 0, paramArray.length);
3 }
4
5 private static void mergeSort(Comparable[] paramArray, int low, int high) {
6 if (low >= high) {
7 return;
8 }
9
10 int mid = low + (high-low)/2;
11 //先对左半部分进行排序
12 mergeSort(paramArray, low, mid);
13
14 //对右半部分排序
15 mergeSort(paramArray, mid+1, high);
16
17 //对排序结果进行归并
18 merge(paramArray, low, mid, high);
19 }
20
对于自顶向下的归并排序,我们可以用下面的树状图来理解其排序过程
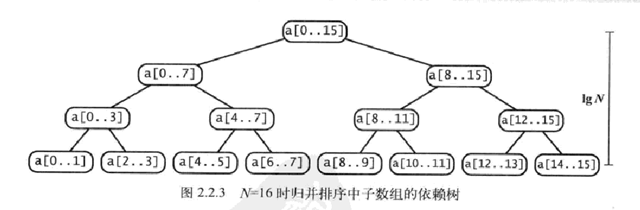

因此自顶向下的归并排序算法的时间复杂度是NlgN。归并排序需要额外的辅助数组空间,其大小也是和输入规模N成正比。
-
自底向上的归并排序
用递归的方法实现归并排序,是一种分治思想的一种典型应用。我们将一个大问题分解成比较小的的问题分别解决,然后用所有小问题的答案来解决大问题。实现归并排序的另外一种方法是先对小的数组分别进行排序,然后再成对的归并小数组,知道将整个数组归并到一起。
1 /*自底向上的归并排序*/
2 public static void mergeSortButtonUp(Comparable[] paramArray) {
3 int N = paramArray.length;
4
5 for (int size=1; size<N; size += size) { //子数组的大小
6 for (int low=0; low<N; low=low+size*2) {
7 merge(paramArray, low, low+size-1, Math.min(low+size*2-1, N));
8 }
9 }
10 }
-
排序算法的时间复杂度

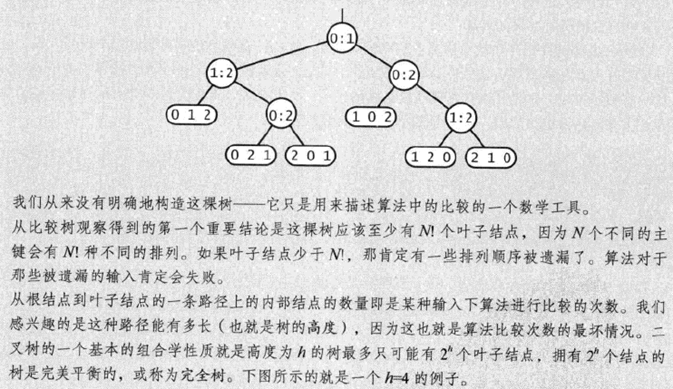

由此可见归并排序是一种渐进最优的基于比较排序的算法。
四、快速排序
快速排序算法的特点是它是一个原地排序算法(只需要一个小的辅助栈),且将规模为N的数组排序需要的时间复杂度是NlgN。
快速排序也是一种利用分治思想排序的方法,其主要算法思想大概如下:给定一个数组paramArray,将该数组切分为两个数组paramArray[low...i],paramArray[i+1...high],使paramArray[low...i]都小于某个元素,paramArray[i+1...high]都大于某个元素。然后将切分后的小数组再进行切分…直到最后被切分的小数组只有一个元素,这时候整个数组就完成了排序。
由此可以看出,快速排序算法的核心算法是切分算法的设计。快速排序的切分算法实现如下:
1 /***********************************************************************
2 * 给定一个数组paramArray,将该数组切分为两个数组paramArray[low...i],paramArray[i+1...high],
3 * 使paramArray[low...i]都小于某个元素,paramArray[i+1...high]都大于某个元素。
4 * 我们的做法是用两个哨兵变量sentry1,sentry2分别从数组的头和尾进行遍历,如果
5 * sentry1比flag大,sentry2比flag小,则对调,直到两个哨兵相遇
6 * *********************************************************************/
7 private static int seperate(Comparable[] paramArray, int low, int high) {
8 int sentry1 = low+1;
9 int sentry2 = high;
10
11 Comparable flag = paramArray[low];
12 while (sentry1<=sentry2) {
13 if (less(paramArray[sentry1], flag)) {
14 sentry1++;
15 continue;
16 }
17 if (less(flag, paramArray[sentry2])) {
18 sentry2--;
19 continue;
20 }
21 exchange(paramArray, sentry1, sentry2);
22 sentry1++;
23 sentry2--;
24 }
25 exchange(paramArray, low, sentry2);
26 return sentry2
基于该切分算法利用递归调用的思想实现的快速排序算法如下:
1 public static void quickSort(Comparable[] paramArray) {
2 quickSort(paramArray, 0, paramArray.length-1);
3 }
4
5 private static void quickSort(Comparable[] paramArray, int low, int high) {
6 if (low >= high) {
7 return;
8 }
9 int seperateLocation = seperate(paramArray, low, high);
10 quickSort(paramArray, low, seperateLocation);
11 quickSort(paramArray, seperateLocation+1, high);
12 }


五、优先队列
-
堆的定义
堆有序:当一棵二叉树的每个节点都大于等于他的两个子节点时,它被称为堆有序。
二叉堆是一组能够用堆有序的完全二叉树排序的元素,并在数组中按照层级存储,(不使用数组的第一个元素)
如果我们用指针来表示堆有序的二叉树,那么每个节点就需要用三个指针来分别指向他的三个连接节点,对于完全二叉树只用数组就可以表示,具体方法就是将二叉树的节点按照层级顺序放入数组,根节点位置在1,而他的子节点的位置在2,3。而子节点的子节点的位置分别在4,5,6,7,以此类推。
(一下简称完全二叉堆为堆)在一个堆中,位置k的父节点位置是k/2,两个子节点的位置分别是2k和2k+1.
-
二叉堆的算法
(1)右下向上的堆有序化(上浮)
如果一个堆的有序状态因为一个节点比他的父节点大而被打破,那么我们就需要通过交换他和她的父节点来修复堆。交换后这个各节点比他的两个子节点都打(一个是曾经的父节点,另一个是原来父节点的子节点),但是交换后,该节点仍然可能比父节点还要大,我们就反复的用相同的方法恢复堆的顺序。只要记住位置k的节点的父节点是k/2。实现如下:
1 private void swim (int k){
2 while (less(cacheArray[k/2], cacheArray[k]) && k>1) {
3 exchange(cacheArray, k/2, k);
4 k = k/2;
5 }
6 }
(2)由上至下的堆的有序化(下沉)
如果对的有序化状态因为某个节点变得比他的子节点小而打破,那么我们可以通过下沉操作来进行堆的有序化。具体操作为:将该节点跟子节点中较大的节点进行对换,交换可能在子节点处继续打破有序化,那么我们就重复上述操作。位置为k的元素,其子节点的位置分别为2k和2k+1.
1
2 private static void sink (int k) {
3 while (2*k <= N) { //N是优先队列的容量
4 int temp = 2*k;
5 if (less(cacheArray[2*k], cacheArray[2*k+1])) {
6 temp = 2*k+1;
7 }
8 if (!less(cacheArray[k], cacheArray[temp])) {
9 break;
10 }
11 exchange(cacheArray, k, temp);
12 }
13 }
(3)插入元素
我们将新元素插入到数组末尾,增加堆的大小并将新插入的元素上浮到合适的位置
1 /*删除最大元素*/
2 public static Comparable delMax() {
3 Comparable max = cacheArray[1]; //从跟节点得到最大元素
4 exchange(cacheArray, 1, N); //将其和最后一个元素交换
5 N--; //队列长度减1
6 cacheArray[N+1] = null; //防止越界
7 sink(1); //恢复队列的有序性
8
9 return max;
10

六、堆排序
堆排序是一种基于优先队列的排序算法,可以分为两个阶段:第一个阶段是将待排序的数组构造成一个堆,然后在下沉排序阶段,我们每次从堆中取出最大元素放到辅助数组中,当堆中的元素被完全取出,排序就完成了。
七、对各种排序的比较
各种排序算法的性能特点如下图





