[AGC052B] Tree Edges XOR
好题,可以直接作为套路记录一下。
[AGC052B] Tree Edges XOR
题目大意:
给你一棵树,有奇数个点,每个边有边权 \(w_i\)。每次你可以选出一条边,将和这条边的所有相邻的边都异或这条边的边权,问你能否得到最终状态(操作次数不定)。
思路:
首先,上来会发现每次操作影响的边十分多,肯定无法直接维护,考虑转化。
操作是异或,那异或有什么性质呢?答案是“某个数异或同一个数两次,数值不变”。
那我们考虑,当我们进行一次操作时,什么由于这个性质是不变的,或是变得很少。
如果某个东西改变的很少,我们就可以转化了。
如下图,如果我们对红色的边进行了操作(有紫色标记的边是被修改的)。
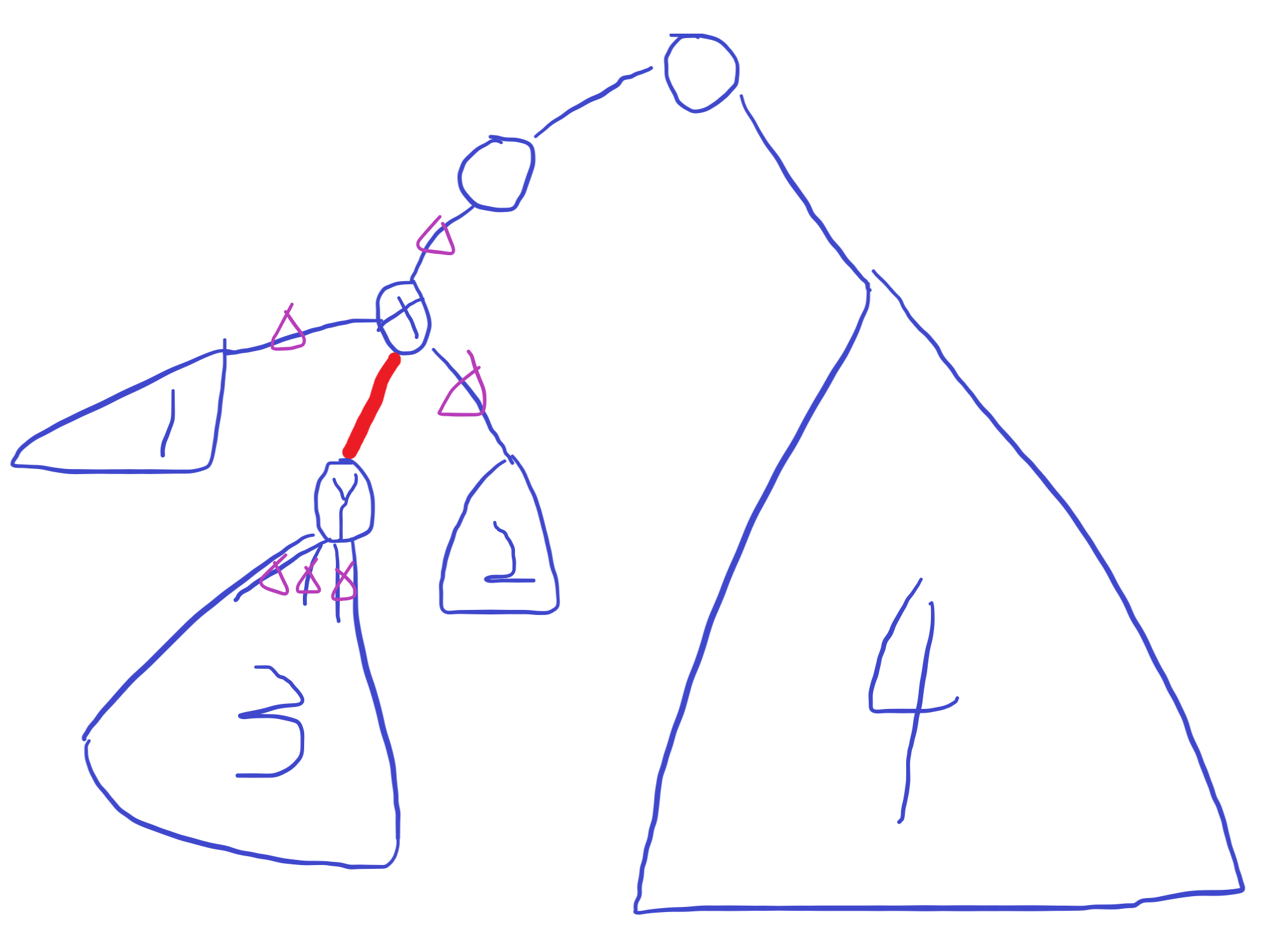
可以发现从根到 \(4\) 号子树的路径没有任何修改,同时根到 \(1\),\(2\),\(3\) 号子树的路径上都有两条边被异或了一次。
所以根到这些点的路径异或和都没有任何改变。
但是进行操作的这条边的两端 \(x\) 和 \(y\),它们的路径异或和有所改变。
我们设这条边的边权为 \(w\),它们原来的路径异或和分别为 \(dis_x\) 和 \(dis_y\),修改后就变成了 \(dis_x'\) 和 \(dis_y'\),我们来看看它们前后之间的关系。
可以发现:
就是将两个数值交换了。
所以我们可以将边权设为到根的路径异或和,每次就是交换两个边的边权。
但是操作边还是不好做,可以直接下放边权为点权,这样题目就变成了“每次交换两个点上的数字,问是否可以达到目标状态”。
那这道题就结束了吗?还没有。
注意到因为我们的点权是到根的路径异或和,所以根节点的值应该一直为 \(0\),但是如果涉及到根节点和它儿子之间的边进行操作的时候,一旦交换根节点的点值,就无法保证根节点是 \(0\) 了。
这是因为根节点上方没有别的边了,所以无法满足性质,那我们可以在加一个虚拟点,向根节点连边,即给根节点一个虚拟的父亲节点,这样,在进行原问题的操作的时候,对周围的所有边进行异或,就也给这条虚拟边进行异或,这样,根节点的性质就也可以被满足了。
到了这一步,还是有问题,就是我们在计算点权的时候,初始状态下虚拟边的 \(w\) 肯定是 \(0\),但是目标状态的权值由于可能会进行多次异或操作,所以不一定是 \(0\)。
那应该是什么呢?
可以发现,转化之后的题目每次就是交换两个点值,不会改变点值,所以点值的种类和数量都不会改变,那么如果最终态可以达到,则初始状态和最终状态的所有数的异或和必然相同。而且由于题目保证了点的数量为奇数,所以在最终状态的所有点的异或和中虚拟边的边权一定是异或了奇数遍。
那我们就可以知道,将初始和目标状态的所有点值的异或和再异或起来,得到的数就是虚拟边的边权,即为原本根节点的点值。
然后再把这个值带回到目标状态,计算出所有的点值,看看是否和初始状态一样就好了。
Code:
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define mod 1000000007
#define lowbit(x) (x&(-x))
inline int read(){
int rt=0; char g=getchar();
while(g<'0'||g>'9') g=getchar();
while(g>='0'&&g<='9') rt=(rt<<3)+(rt<<1)+g-'0',g=getchar();
return rt;
}
int n,w[2],qwq;
int dis[2][100005];
struct node{int to,w[2];};
vector<node>t[100005];
inline void dfs(int now,int fa,int opt)
{
w[opt]^=dis[opt][now];
for(int i=0,to;i<t[now].size();i++)
{
to=t[now][i].to; if(to==fa) continue;
dis[opt][to]=dis[opt][now]^t[now][i].w[opt];
dfs(to,now,opt);
}
}
int main()
{
n=read();
for(int i=1,u,v,w1,w2;i<n;i++)
{
u=read(),v=read(),w1=read(),w2=read();
t[u].push_back({v,w1,w2});
t[v].push_back({u,w1,w2});
}
dfs(1,0,0); dfs(1,0,1); qwq=w[0]^w[1];
for(int i=1;i<=n;i++) dis[1][i]^=qwq;
sort(dis[0]+1,dis[0]+1+n);
sort(dis[1]+1,dis[1]+1+n);
for(int i=1;i<=n;i++) if(dis[0][i]!=dis[1][i]) return puts("NO"),0;
puts("YES");
return 0;
}


