P9746 「KDOI-06-S」合并序列
mx练习赛搬的,虽然数据不咋样,但是一步步的优化思路确实值得一记。
P9746 合并序列
题目大意:
给你 个数 ()。每次可以选一个3元组 ,满足 ,并且 ,则你可以将 删掉并替换为 。
请你判断是否能够使得序列 仅剩一个数。若可以,你还需要给出一种操作方案。
( 表示按位异或运算)
思路:
1. 区间dp
首先,可以看到 ,我们可以想到区间 。
我们设 为区间 是否 可以被消掉, 为区间 的异或和,那么我们有以下转移:
这样的话预处理 是 的,然后转移是 的,还要优化。
虽然数据弱的你剪剪枝不一定不过,但是你肯定不敢写
好歹这玩意是六次方,你肯定不信这玩意是正解
2. 优化
我i们会发现题目的 给的很小,和 是一个级别的,这个性质我们还没有用到,那么我们往值域上考虑。
考虑到异或和为零就意味着异或的两个数是相等的,所以如果你确定了两个区间,那么就意味着剩下的一个区间的异或的值就已经确定了。
那么我们设 为区间 之间是否存在异或和为 的可行(相应 为 )的区间。
那么转移就变成了:
这样的话,转移就会是 的。
但是理论上还是过不去的,毕竟 和值域都是 ,还要乘上 ,但是数据……
2. 优化(二阶段)
如果我们再顺着上面的思路去想,会发现好像实在是没法优化了,考虑转换 状态和枚举的东西。
首先,如果我们如果想要降低复杂度的话,一定要想用最少的枚举确定多个信息。
那它是什么呢?异或!
异或和为 的充要条件就是两个数相等。那我们可以枚举一个 ,表示某两个区间的异或和,和第三个区间的值,这两个值必须是相同的。
所以我们可以用这个性质将三个区间分成两份,不妨让前两个一起考虑,最后一个单独考虑。
这样我们就把区间分成了两份。
我们可以枚举 ,代表当前我在判断哪个区间可行,它的两部分的异或和是多少。
但是转移的话如果还是用之前的数组好像难以快速解决问题,我们考虑再优化。
有一个套路, 的时候如果状态只是记录可行性,可以考虑将某一维变成存储的值,记录在可行的条件下最优情况。
首先, 显然是省不了的,也没必要省。
但是我们可以发现, 数组一看就很傻是吧,只是维护一个区间内是否存在就很浪费,我们可以将他变为 ,意义是对于左端点 的点,异或值为 的可行区间的右端点的最小值。
这样,在判断当前是否可行的时候,只要这个最小值和右边枚举的区间不交就行。
同时,我们会发现,同样的,枚举的 这个区间……
插一下区间关系:
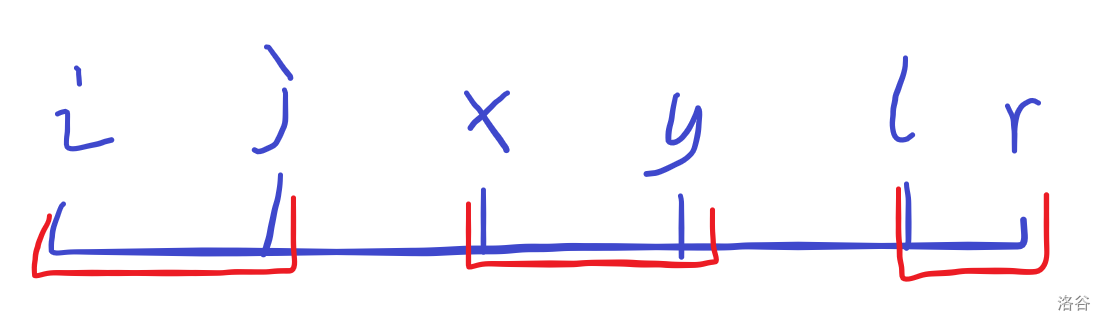
也很蠢,我们也可以设数组 ,记录右端点等于,异或值是 ,最大的 是多少。
但是,如果只是变了这几个数组,还是无法降低复杂度,因为你至少还要枚举一个 。
我们会想到,既然已经将前两个区间分为一组了,那我们直接记录 左端点 等于,包含两个可行区间,最小的右端点是多少。
这样的话,转移的时候就直接枚举 ,只要 和 不交,那就说明区间 可行。
一定注意一下枚举顺序,由于我们在判断当前区间的时候需要用当前区间左端点之后的信息,所以要倒序枚举 ,然后又因为需要用到当前区间内的小区间的信息,所以正序枚举一个 的 。
这样转移就是 的,再看一下 数组的维护。
首先 和 都很好维护。
直接可以从 继承,然后每找到一个可行区间就更新。
由于要卡到右端点,所以更简单,直接不停取 就好了。
但是, 呢?
我们会发现由于 记录的是左端点等于 的两个区间,所以当我们找到一个合法区间的时候,都要进行更新,这是动态的,因为我们对于某个确定的 ,我们都有可能要用刚刚找到的可行区间来更新之后的区间。
你可能会想到,区间的判定就已经是 的了,每次确定了一个区间之后又要用 的枚举配合 来求解,这样不就是 的了吗?
但其实会发现,可行的区间最多只有 种,所以我们只会动态更新 数组 次,每次是 的,所以复杂度就是 的。
这里一定要注意,为了保证 的复杂度,一定要在判断出当前区间合法时直接退出循环,保证 数组只会动态更新 次。
所以,最终复杂度 ,理论上的正解。虽然跑的不一定比暴力快。
Code:
#include<bits/stdc++.h>
using namespace std;
inline int read(){
int rt=0; char g=getchar();
while(g<'0'||g>'9') g=getchar();
while(g>='0'&&g<='9') rt=(rt<<3)+(rt<<1)+g-'0',g=getchar();
return rt;
}
int a[505],sum[505][505];
bool f[505][505];
int net[505][512],lst[505][512];
int g[505][512],gans[505][512];
struct node{int i,j,x,y,l,r;}fans[505][505];
int ans[505][505];
struct nnode{int l,r;}netans[505][512];
int num;
inline void out(int l,int r)
{
if(l==r) return;
register int A,B,C;
A=fans[l][r].i-num;out(fans[l][r].i,fans[l][r].j);
B=fans[l][r].x-num;out(fans[l][r].x,fans[l][r].y);
C=fans[l][r].l-num;out(fans[l][r].l,fans[l][r].r);
printf("%d %d %d\n",A,B,C); num+=C-A;
}
int main()
{
register int T=read(),n;
register int i,j,k,l,r;
while(T--)
{
n=read(); memset(f,0,sizeof(f));
for(i=0;i<512;i++) g[n+1][i]=gans[n+1][i]=n+1;
for(i=1;i<=n;i++)
{
a[i]=read(),f[i][i]=1;
for(j=1;j<=i;j++) sum[j][i]=sum[j][i-1]^a[i];
for(j=0;j<512;j++) net[i][j]=n+1,lst[i][j]=0;
}
for(l=n;l;l--)
{
memcpy(g[l],g[l+1],sizeof(g[l+1]));
memcpy(gans[l],gans[l+1],sizeof(gans[l+1]));
g[l][a[l]]=gans[l][a[l]]=lst[l][a[l]]=l;
for(j=0;j<512;j++)
if(net[l][j^a[l]]>g[l+1][j])
net[l][j^a[l]]=g[l+1][j],netans[l][j^a[l]]={l,gans[l+1][j]};
for(r=l+2;r<=n;r++)
for(j=0;j<512;j++)
if(net[l][j]<lst[r][j])
{
ans[l][r]=ans[l][netans[l][j].l]+ans[netans[l][j].r][net[l][j]]+ans[lst[r][j]][r]+1,
f[l][r]=1,fans[l][r]={l,netans[l][j].l,netans[l][j].r,net[l][j],lst[r][j],r};
lst[r][sum[l][r]]=max(lst[r][sum[l][r]],l);
if(g[l][sum[l][r]]>r) g[l][sum[l][r]]=r,gans[l][sum[l][r]]=l;
for(k=0;k<512;k++)
if(net[l][k^sum[l][r]]>g[r+1][k])
net[l][k^sum[l][r]]=g[r+1][k],netans[l][k^sum[l][r]]={r,gans[r+1][k]};
break;
}
}
if(f[1][n]){printf("Huoyu\n%d\n",ans[1][n]);num=0;out(1,n);}
else puts("Shuiniao");
}
return 0;
}



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 地球OL攻略 —— 某应届生求职总结
· 周边上新:园子的第一款马克杯温暖上架
· Open-Sora 2.0 重磅开源!
· 提示词工程——AI应用必不可少的技术
· .NET周刊【3月第1期 2025-03-02】