CF1473E

分层图的妙用。

CF1473E

题目大意：

双向图，对于某一条路径的权值的计算方式为 \(\sum_{i=1}^{k}w_i-\max w_i+\min w_i\)，问从1号节点出发的最短路。

思路：

1. 转化：

真的是，在做题目的时候不要看到 \(max\) 和 \(min\) 加加减减就想差值最大最小，也有可能就是单纯的全翻倍之后答案不变。

就像这个题目，加min和减max都是可以贪心的，本质上还是求最短，又由于单源最短路的依据基本都是贪心，就可以转化成：

路径上某一条边长度翻倍，某一条边的长度清零，问最短路。

这时候就会发现，由于是最短路，且限制同为贪心，所以这样求出来的最终答案和要求的一致（显然，可以意会一下）。

那么，这样就变成了分层图模板题目：

有两个特殊操作，要求每个只进行固定个数（1）次，问最短路。

不过，还是有一点差异的，就是注意到这两个操作之间还有一个顺序问题，所以要建两种图：

对于每一条边：

1. 第一层边权 \(\times 2\) 连向第二层，第二层边权为0连向第三层。
2. 第一层边权为0连向第二层，第二层边权 \(\times 2\) 连向第三层。

当然，首尾是可以合并的，合并之后的最终关系如下图：

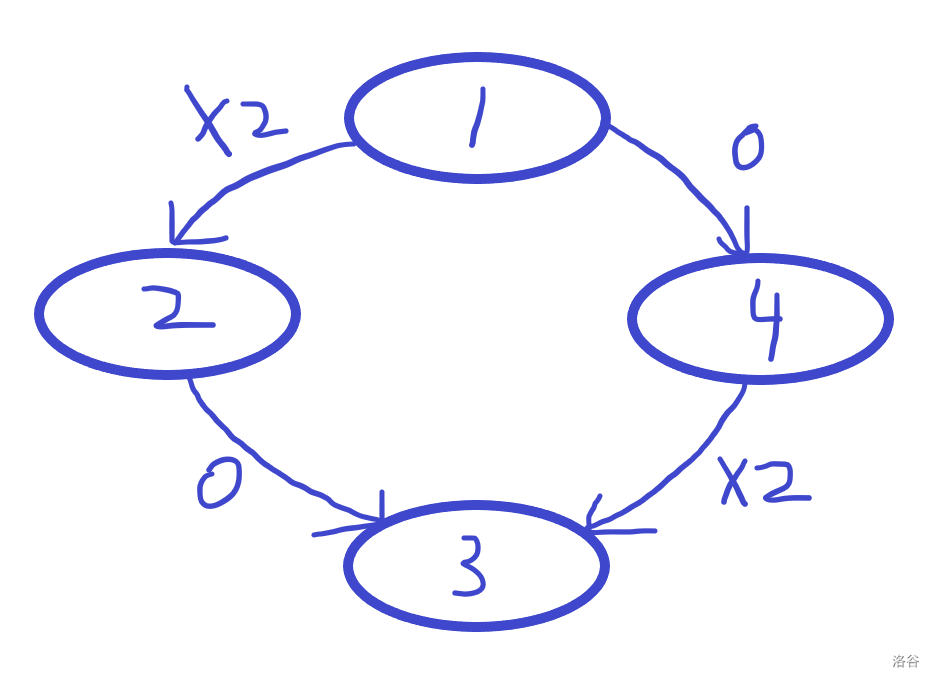
2. 细节：

1. 特殊情况：

当某一条路径上只有一条边的时候（即从1直接连向其余点），max和min为同一个，所以会抵消，但是建立的分层图就导致走到最终节点时至少会走两条边。

解决方法就是特判，当某一条边的端点有1时，单独连一条从第一层的1连向这条边非1的节点的第三层的相应节点（单向）。

if(u>v)	swap(u,v);
if(u==1)	t[u].push_back({2*n+v,w});

2. 记得是双向边

Code：

#include<bits/stdc++.h>
using namespace std;
#define ll long long
inline int read(){
	int rt=0;	char g=getchar();
	while(g<'0'||g>'9')	g=getchar();
	while(g>='0'&&g<='9')	rt=(rt<<3)+(rt<<1)+g-'0',g=getchar();
	return rt;
}
int n,m;
struct node{int to;ll w;};
vector<node>t[800005];

bool ck[800005];
ll dis[800005],w;
struct nnode{int now;ll dis;};
bool operator<(nnode A,nnode B){return A.dis>B.dis;}
priority_queue<nnode>q;
inline void dij()
{
	memset(dis,0x3f,sizeof(dis));
	dis[1]=0;	q.push({1,0});
	int now;
	while(!q.empty())
	{
		now=q.top().now;	q.pop();
		if(ck[now])	continue;
		ck[now]=1;
		for(int i=0,to;i<t[now].size();i++)
		{
			to=t[now][i].to;	w=t[now][i].w;
			if(dis[to]>dis[now]+w)
			{
				dis[to]=dis[now]+w;
				q.push({to,dis[to]});
			}
		}
	}
}
int main()
{
//	freopen(".in","r",stdin);
//	freopen(".out","w",stdout);
	n=read();m=read();
	for(int i=1,u,v;i<=m;i++)
	{
		u=read();v=read();w=read();
		
		t[u].push_back({v,w});
		t[n+u].push_back({n+v,w});
		t[2*n+u].push_back({2*n+v,w});
		t[3*n+u].push_back({3*n+v,w});
		t[v].push_back({u,w});
		t[n+v].push_back({n+u,w});
		t[2*n+v].push_back({2*n+u,w});
		t[3*n+v].push_back({3*n+u,w});
		
		
		t[u].push_back({n+v,w<<1});
		t[u].push_back({3*n+v,0});
		t[n+u].push_back({2*n+v,0});
		t[3*n+u].push_back({2*n+v,w<<1});
		
		
		t[v].push_back({n+u,w<<1});
		t[v].push_back({3*n+u,0});
		t[n+v].push_back({2*n+u,0});
		t[3*n+v].push_back({2*n+u,w<<1});
		
        if(u>v)	swap(u,v);
        if(u==1)	t[u].push_back({2*n+v,w});
	}
	dij();
	for(int i=2*n+2;i<=3*n;i++)	printf("%lld ",dis[i]);
	return 0;
}