并查集的特殊运用
我之前对于这种题目一直都是选择自己想的“3染色DFS”,没想到还可以用并查集来做,长见识了。
P2661 [NOIP2015 提高组] 信息传递
题目大意:
每个点只有一条出边,问最小环是多大。
思路:
- “自己的发明”
- 并查集
1. “3染色DFS”
一直是用这个做,但现在会不一样的了!!!
2. 并查集
上来可能会想不明白,这个建立的是单向边,为什么可以用并查集呢?
答案就是这类问题很特殊:每个点只有一个出边。
这就导致了一旦形成环的话,就一定是个基环树。
并且,在形成环之前,这就一定是一棵内向树。
这就保证了如果直接用并查集维护的话,会有这两个性质:
- 只有在形成环的时候会出现同一连通块相连的情况。
- 在形成环之后整个连通块就形成闭环,再也不会产生操作。
这是因为整个连通块(内向树)里面,只有根节点没有出边,所以在连边操作一定是从根节点出发的,如果连到自己这个连通块的点的话就是环,如果是别的连通块,就是连通块合并。而且合并之后整个连通块还一定是一个内向树。
如果形成环,那么这个连通块的所有点就都有出边了,所以再也不会有操作了。
所以当出现环的时候,就可以相当于直接将整个连通块的点删除。所以只会留下内向树。
正因为无论什么时候这个图都一定是内向树森林,所以用并查集维护是没有问题的。
可以配合下图理解(意会):
- 形成环:
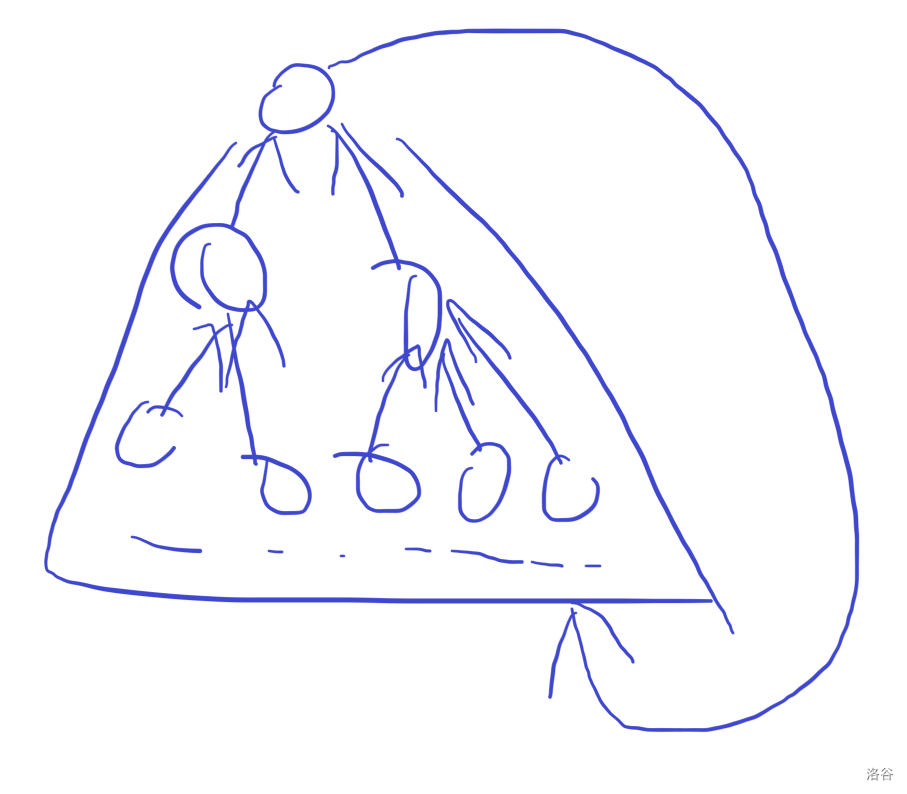
- 连向别的连通块。
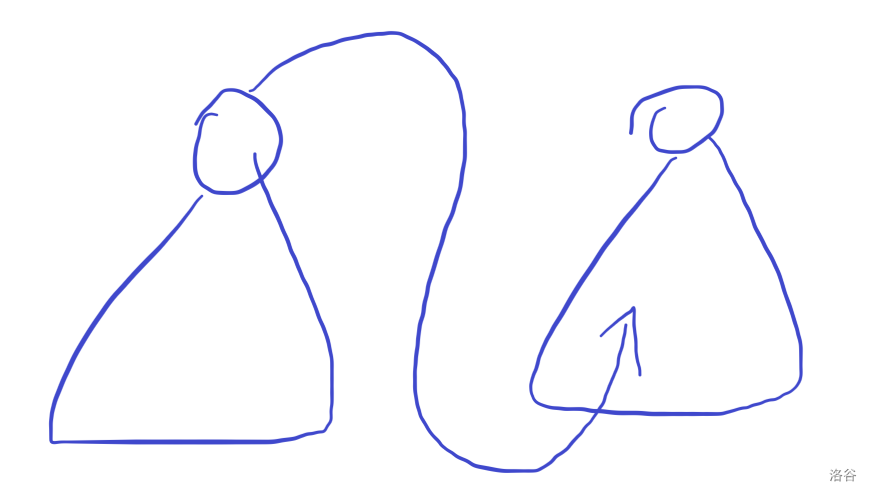
既然我们可以用并查集维护的正确性没有问题,那只有最后一个问题:
怎么记录环的长度?
答案很简单,我们可以记录每个节点到根节点的距离 \(len_i\),在形成环的时候就可以轻松统计环的长度(相连两点的 len 相加 +1 )。
然后我们在维护的时候只需要在路径压缩的时候确保了len的正确性就好了(具体看代码)。
Code:
#include<bits/stdc++.h>
using namespace std;
inline int read(){
int rt=0; char g=getchar();
while(g<'0'||g>'9') g=getchar();
while(g>='0'&&g<='9') rt=(rt<<3)+(rt<<1)+g-'0',g=getchar();
return rt;
}
int n,ans;
int a[200005];
int len[200005];
inline int BOSS(int A)
{
if(a[A]!=A)
{
int lst=a[A];
a[A]=BOSS(a[A]);
len[A]+=len[lst];
}
return a[A];
}
inline void check(int A,int B)
{
int AA=BOSS(A),BB=BOSS(B);
if(AA==BB) ans=min(ans,len[A]+len[B]+1);
else
{
len[AA]=len[B]+1;
a[AA]=BB;
}
}
int main()
{
n=ans=read();
for(int i=1;i<=n;i++) a[i]=i;
for(int i=1,to;i<=n;i++) check(i,read());
printf("%d",ans);
return 0;
}


