P1600 [NOIP2016 提高组] 天天爱跑步
之前就听说是好题,就想做,现在做完了,果然是好题。
P1600 天天爱跑步
题目大意:
给你一棵 \(n\) 个节点的树,\(m\) 个任务。
每一个任务有起点和终点,沿树上最短路径,都从 \(0\) 秒开始,每秒瞬移到下一个点。
每个节点有一个值 \(w\),代表当前节点会在 \(w\) 秒的时候统计当前节点一共有对少人。
问每个结点的答案。
思路:
1.转换
首先,上来会发现,这个任务相互之间是不可合并的,所以显然无法用树上差分之类的东西维护,所以无法直接做,考虑转化。
那么我们考虑对于每个点,统计对当前这个点有贡献的任务有多少。
显然,可以发现,如果一个任务对于当前节点有贡献的话,这个点一定是被夹在起始点或者结束点与它们的 \(lca\) 之间的,如下图:
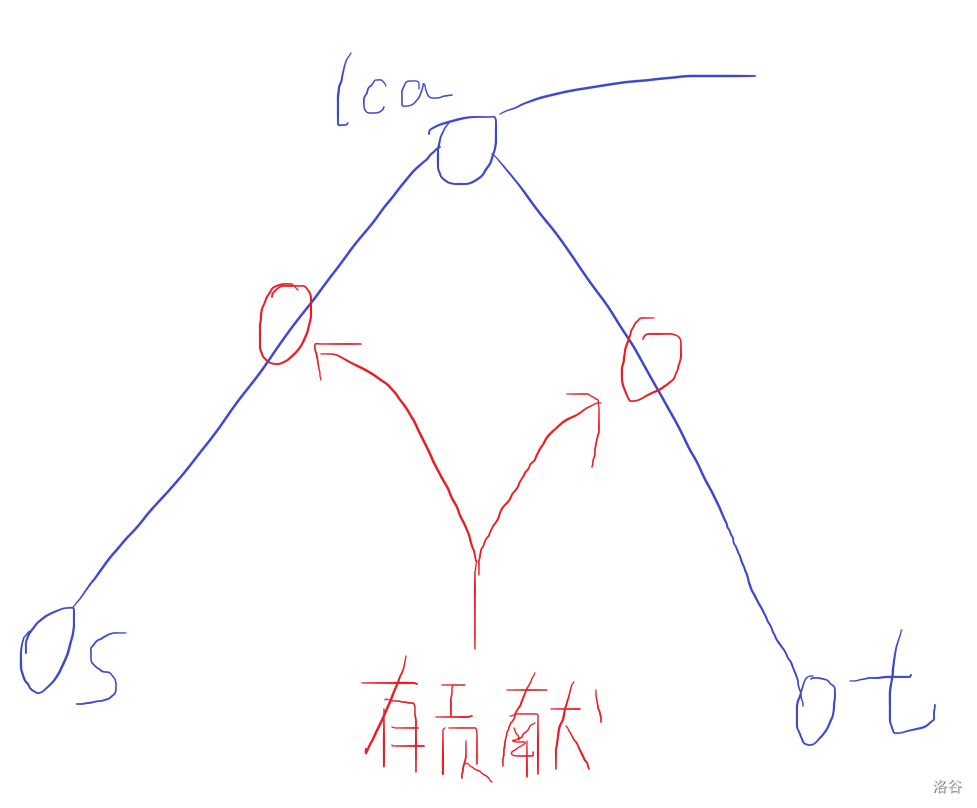
(\(s\) 和 \(t\) 分别为起点和终点,\(lca\) 就是 \(s\) 和 \(t\) 的 \(lca\))
(求 \(lca\) 就不说了,有的是方法)
会发现,对某一点有贡献的任务一定是起点或者终点在这个点的子树中。
并且利用深度 \(dep\) 转化之后,我们可以发现,如果对某一点(设为 \(p\))有贡献,一定是:
- \(dep_s=dep_p+w_p\)
- \(len-dep_t=w_p-dep_p\)
(\(len\) 是 \(s\),\(t\) 之间的距离,就等于\(dep_s+dep_t-dep_{lca}\times 2\))
综上,就会发现有一个优美的性质,由于对某一点有贡献的任务一定是起点或者终点在这个点的子树中,并且经过转化后,每一个点作为起点或终点就独立了,所以我们可以对于每一个子树都作为子问题单独处理。
并且,又因为每个任务的起点和终点独立且做贡献的时候式子唯一,我们可以开两个桶 \(b1\) 和 \(b2\),分别记录当前子树中的所有起点的 \(dep_s\) 和所有终点的 \(len-dep_t\) 的数量。
具体操作的时候,我们可以对于每个点开两个vector,记录所有以当前点作为起点的所有 \(dep_s\) 和作为终点的所有 \(len-dep_t\) 。
又因为作为起点的话,都是对桶的 \(dep_s\) 有贡献,所以可以直接统计某一点作为起点的数量就好了,就没必要开vector了。
递归到某一点将当前点的贡献加入桶中就彳亍了。
注意,由于在作为终点做贡献的时候会减出负数,所以可以统一加上一个大数防止溢出。
//递归到某个点
inline void dfs2(int now)
{
…………
……
b1[dep[now]]+=st[now];
for(int i=0;i<ed[now].size();i++)
b2[ed[now][i]-dep[now]+ADD]++;
…………
}
……
…………
int main()
{
…………
……
//读入
int u,v,lca,dist;
while(m--)
{
u=read(); v=read();
lca=LCA(u,v); dist=dep[u]+dep[v]-(dep[lca]<<1);
……
…………
st[u]++;
ed[v].push_back(dist);
}
……
…
}
2. 桶的使用
对于桶的使用,其实是有一个问题的。就是对于已经统计过的部分,无法保证只有当前树的子树,如下图:
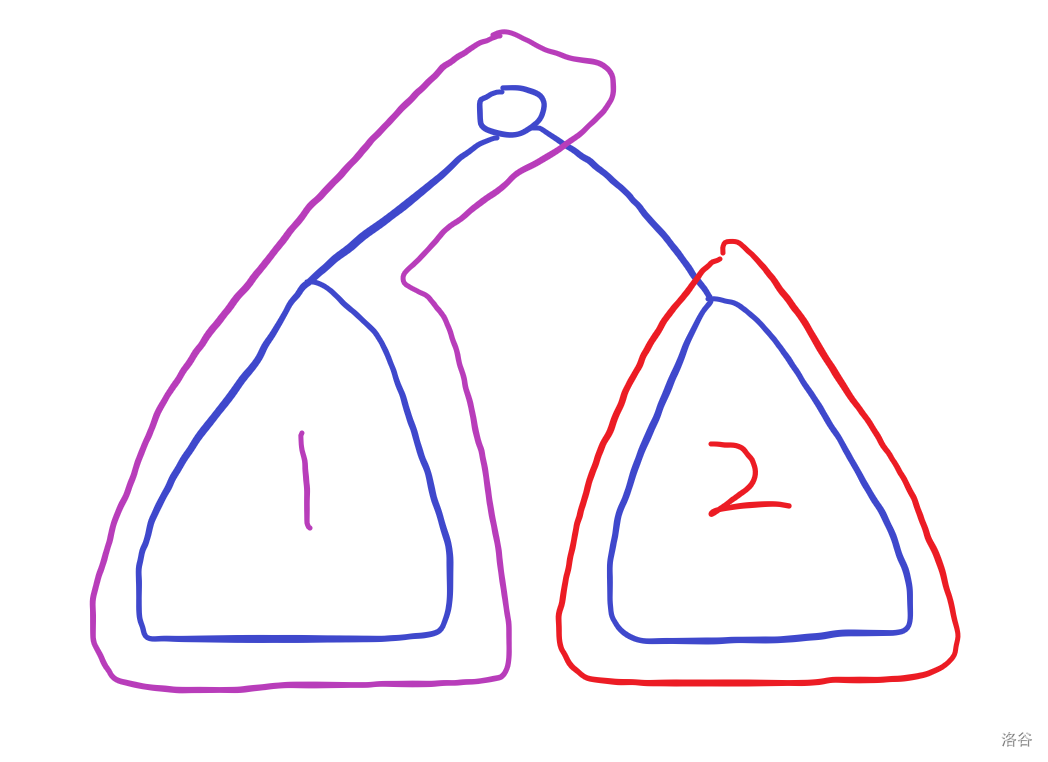
在枚举到2子树时,1已经全部枚举完了,并且贡献都在桶中了,但是这一部分在统计2的答案的时候,不应该在桶里。
可要是都去除的话又不好,因为这一部分在统计整个树时候要用到,全部分开然后合并重算太费时间和空间。
怎么办呢?会发现对于某一棵子树,它的遍历是连续的(这也是几乎所有和子树有关的题目的做法依据),就是在刚进入这个点开始,到离开这个点结束,一定完全且只遍历了这个点的子树。
所以可以在刚刚进入这个点的时候,记录要统计的、桶内的贡献 \(num1\) 和 \(num2\),之后在遍历完它的整个子树之后,将它们与现在的桶内贡献做差,就得到了这个子树内新增的贡献。
inline void dfs2(int now)
{
int num1=b1[dep[now]+w[now]],num2=b2[w[now]-dep[now]+ADD];
…………
……………… //遍历子树
…………
ans[now]+= (b1[dep[now]+w[now]]-num1) +
(b2[w[now]-dep[now]+ADD]-num2);
……
}
3. 多余贡献
然后注意由于 \(p\) 必须是在 \(s\) 或 \(t\) 与 \(lca\) 之间,所以如果当前任务的 \(lca\) 在当前子树的内部,那么它就再也没有贡献了。(可以看图意会一下)
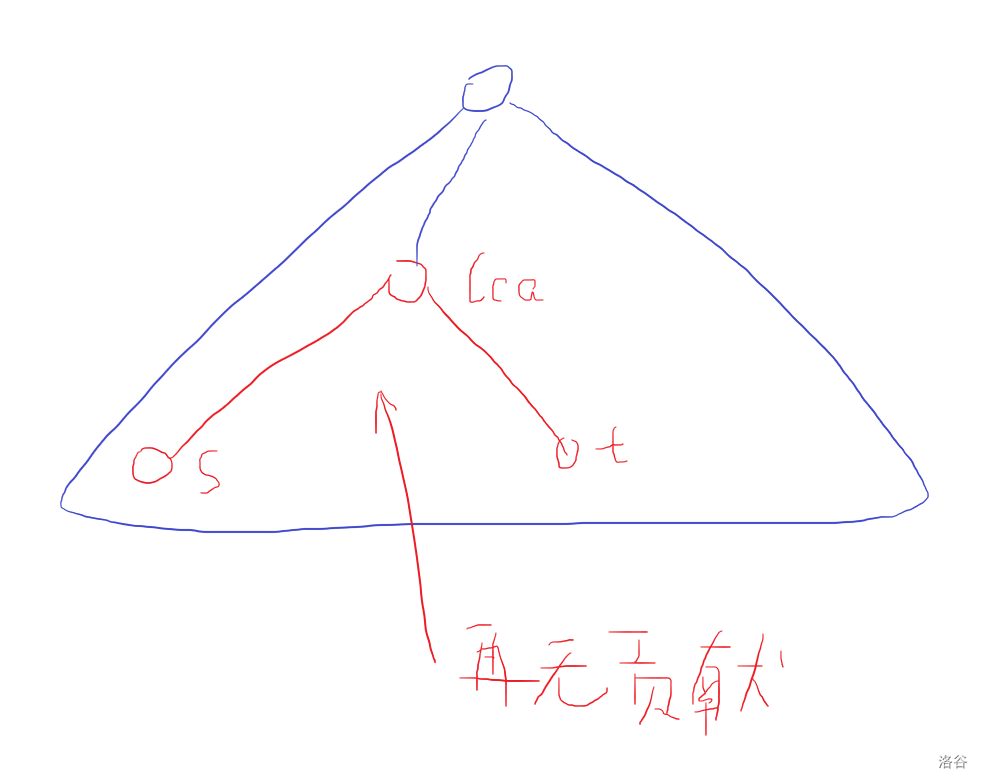
对于这种任务,我们需要在桶内去除它的贡献。
可以发现,这种任务最后的贡献是在 \(p\) 即为 \(lca\) 的时候,之后就再不可能有贡献。所以,在递归的时候,可以对于所有 \(lca\) 为当前点的任务从桶中去除。
具体操作的时候可以对于每个点都开一个vector,存储所有以当前点为 \(lca\) 的任务,在统计完这个点的答案之后将这些任务去除就好了。
inline void dfs2(int now)
{
…………
……
…………
……
for(int i=0;i<lst[now].size();i++)
{
b1[dep[lst[now][i].s]]--;
b2[lst[now][i].dist-dep[lst[now][i].t]+ADD]--;
}
}
……
…………
int main()
{
…………
……
//读入
int u,v,lca,dist;
while(m--)
{
……
lst[lca].push_back({u,v,dist});
……
}
……
…
}
4. 重复贡献
还有一种情况,就是在某一个任务对于 \(s\) 和 \(t\) 的 \(lca\) 有贡献的时候,这个贡献会计算两次,所以进行特判。
产生的原因可以靠下图意会,就是相当于两个红点合二为一了。当然通过转换后的式子也可以发现。

具体操作时其实很简单,就只需要在读入的时候减掉就好了。
int main()
{
…………
……
//读入
int u,v,lca,dist;
while(m--)
{
……
ans[lca]-=(dep[u]==w[lca]+dep[lca]);
……
}
……
…
}
Code:
#include<bits/stdc++.h>
using namespace std;
#define ll long long
inline int read(){
int rt=0; char g=getchar();
while(g<'0'||g>'9') g=getchar();
while(g>='0'&&g<='9') rt=(rt<<3)+(rt<<1)+g-'0',g=getchar();
return rt;
}
int n,m;
vector<int>t[300005];
int f[300005][19];
int dep[300005];
inline void dfs(int now,int fa,int deep)
{
f[now][0]=fa; dep[now]=deep;
for(int i=0,to;i<t[now].size();i++)
{
if(t[now][i]==fa) continue;
dfs(t[now][i],now,deep+1);
}
}
inline void init()
{
for(register int j=1;j<=18;j++)
for(register int i=1;i<=n;i++)
f[i][j]=f[f[i][j-1]][j-1];
}
inline int LCA(int x,int y)
{
if(dep[x]<dep[y]) swap(x,y);
for(int i=18;i>=0;i--)
if(dep[f[x][i]]>=dep[y])
x=f[x][i];
if(x==y) return x;
for(int i=18;i>=0;i--)
if(f[x][i]!=f[y][i])
x=f[x][i],y=f[y][i];
return f[x][0];
}
int w[300005];
int st[300005];
vector<int>ed[300005];
struct node{int s,t,dist;};
vector<node>lst[300005];
#define ADD 300000
int ans[300005];
int b1[300005],b2[600010];
inline void dfs2(int now)
{
int num1=b1[dep[now]+w[now]],num2=b2[w[now]-dep[now]+ADD];
for(int i=0,to;i<t[now].size();i++)
{
if(t[now][i]==f[now][0]) continue;
dfs2(t[now][i]);
}
b1[dep[now]]+=st[now];
for(int i=0;i<ed[now].size();i++)
b2[ed[now][i]-dep[now]+ADD]++;
ans[now]+=b1[dep[now]+w[now]]-num1+b2[w[now]-dep[now]+ADD]-num2;
for(int i=0;i<lst[now].size();i++)
{
b1[dep[lst[now][i].s]]--;
b2[lst[now][i].dist-dep[lst[now][i].t]+ADD]--;
}
}
int main()
{
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
n=read();m=read();
for(int i=1,u,v;i<n;i++)
{
u=read(); v=read();
t[u].push_back(v);
t[v].push_back(u);
}
dfs(1,0,1); init();
for(int i=1;i<=n;i++) w[i]=read();
int u,v,lca,dist;
while(m--)
{
u=read(); v=read();
lca=LCA(u,v); dist=dep[u]+dep[v]-(dep[lca]<<1);
lst[lca].push_back({u,v,dist});
ans[lca]-=(dep[u]-dep[lca]==w[lca]);
st[u]++;
ed[v].push_back(dist);
}
dfs2(1);
for(int i=1;i<=n;i++) printf("%d ",ans[i]);
return 0;
}

