详解树状数组(各种花活)
之前一直以为树状数组十分局限,最多就是“单点查询+区间修改”或者是“单点加+区间查询”,没想到可以“区间加+区间修改”,快记一下awa。
树状数组
树状数组的应用
- 树状数组模板(单点+区间)
- 树状数组 pro(区间+区间)
- 树状数组 pro max(单点+高维区间)
- 树状数组 pro max plus(高维区间+高维区间)
- 树状数组上二分
树状数组模板(单点+区间)
原理:
树状数组最基础的应用,网上有很多讲解的。大致原理就是对于树状数组上的某一节点 $ i $ ,它记录的信息就是 $ [ i - 2^{lowbit(i)} + 1 \text{,}i ] $ 的和。
比如说 $ 6 $ ,它的二进制就是 $ 110 $,就意味着 $ 6 $ 号节点的信息就是$ [ 6 - 2^{lowbit(6)} + 1 \text{,}6 ] = [ 6 - 2 + 1 \text{,}6 ] = [ 5 \text{,} 6 ] $ 的和。
( \(lowbit(x)\) 是求 \(x\) 的最低的,二进制位为1的数,原理就不细讲了,你只要知道由于计算机存储负数的底层原理, \(lowbit(x)=(x \& (-x))\) )
放个图以供理解:
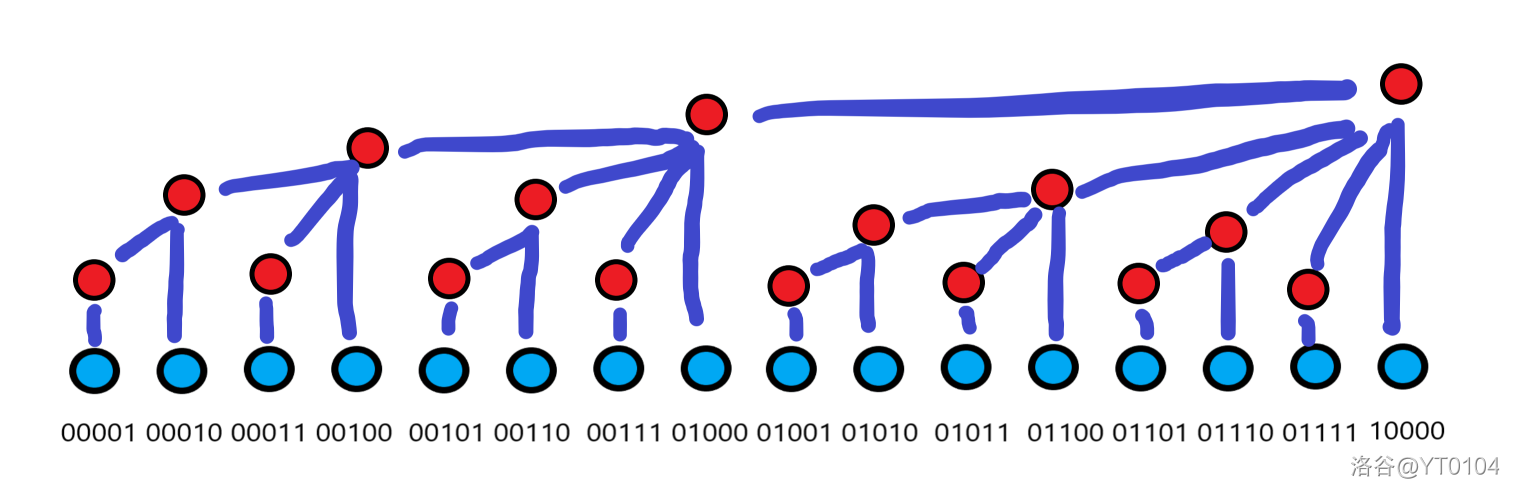
那么我们就可以通过以下(见Code)的方式来做到 \(O(\log n)\) 的修改和查询。
然后现在我们可以做到单点修改,区间查询(查询 \([1,k]\) 的区间和)
同时对于区间修改,单点查询的话可以利用差分,转化成单点修改,区间查询。
注意,我们只能实现查询 \([1,k]\) 的区间和,所以在查询 \([l,r]\) 的时候可以 \(sum(r)-sum(l-1)\)。
Code:
#define lowbit(x) (x&(-x))
int t[1000005];
inline void add(int x,int k)
{
while(x<=n)
{
t[x]+=k;
x+=lowbit(x);
}
}
inline int sum(int x)
{
int rt=0;
while(x)
{
rt+=t[x];
x-=lowbit(x);
}
return rt;
}
相应题目:
树状数组 pro(区间+区间)
好了,开始玩花活
我们已经知道树状数组可以“单点+区间”,那么树状数组怎么“区间+区间”呢?
原理:
首先,对于区间修改,我们可以套路化的将其用差分转化为单点修改。
即:\([l,r]\) 区间加 \(x\),就可以转换成在差分数组(设为 \(t\) )上,\(t_l+=x\) 和 \(t_{r+1}-=x\)。
这样,对于数组 \(i\) 这个位置上的数字的真实值就应该是 \(a_i=\sum_{j=1}^i t_j\)。
其次,对于区间求和,即对于区间\([l,r]\) 的和,我们可以转化成 \(sum(r)-sum(l-1)\),这样我们就将问题转化成了求前缀和 \(ans=\sum_{i=1}^k a_j\) 即可。
因为 \(ans=\sum_{i=1}^k a_j\),又 \(a_i=\sum_{j=1}^i t_j\)。
所以:
可以发现(实在不会拆就用手模几组小的):
但是上面这个和 \(k\) 的关联性很强,无法快速的处理,那我们再转化:
转化成这样,我们就可以求解了。
我们建两棵树状数组,支持单点加,区间求和。
一棵维护 \(\sum_{i=1}^k t_i\),另一棵维护 \(\sum_{i=1}^k (t_i\times(i-1))\)。
Code:
struct node{
ll t[100005];
void jia(int x,ll k){while(x<=n)t[x]+=k,x+=lowbit(x);}
ll SUM(int x){ll rt=0;while(x)rt+=t[x],x^=lowbit(x);return rt;}
}t1,t2; //t1维护区间和 t2维护 *(i-1) 之后的区间和
inline void add(int l,int r,ll k)
{
t1.jia(l,k); t1.jia(r+1,-k);
t2.jia(l,k*(l-1)); t2.jia(r+1,-k*r);
}
inline ll asksum(int k){return t1.SUM(k)*k-t2.SUM(k);}//求[1,k]的区间和
相关题目:
(虽然说是叫线段树,但是可以用升级版的树状数组解)
树状数组 pro max(单点+高维区间)
普通树状数组的拓展
原理:
和普通的树状数组一样,就是多了几维,直接看代码就好了。
同样可以通过多维前缀和将“单点修改+高维区间和”和“单点查询+高维区间修改”相互转化。
我这里用二维来举例子。
Code:
inline void add(int x,int y,int k)
{
for(int i=x;i<=n;i+=lowbit(i))
for(int j=y;j<=m;j+=lowbit(j))
t[i][j]+=k;
}
inline int asksum(int x,int y)
{
int rt=0;
for(int i=x;i;i-=lowbit(i))
for(int j=y;j;j-=lowbit(j))
rt+=t[i][j];
return rt;
}
相关题目:
暂时没有,咕咕咕
树状数组 pro max plus(高维区间+高维区间)
(花活的极致升华(bushi)
这就已经是通法了,其实就是前几种花活综合起来的灵活运用。
我这里还是用二维来举例子。
原理:
首先,还是老套路,老老实实区间加 \(k\) 显然不行,要通过二位前缀和来转化。\((x_1,y_1,x_2,y_2)\) 区间加 \(k\) 就转化成 \(t_{x_1,y_1}+=k\ \ ,\ \ t_{x_1,y_2+1}-=k\ \ ,\ \ t_{x_2+1,y_1}-=k\ \ ,\ \ t_{x_2+1,y_2+1}+=k\)。
则,对于某个点,它真实的值就是 \(a_{x,y}=\sum_{i=1}^{x}\sum_{j=1}^{y}t_{i,j}\)。
同时对于区间求和,我们也可以套路的转化成 \(ans=sum_{x_2,y_2}-sum_{x_2,y_1-1}-sum_{x_1-1,y_2}+sum_{x_1-1,y_1-1}\)(\(sum_{i,j}\) 表示 \((i,j)\) 的二位前缀和)。
所以我们只需要求 \((x,y)\) 的二位前缀和 \(sum_{x,y}\) 就行了。
并且综上:
而拆开后就是:
再展开就变成:
然后,我们设:
那么:
所以我们要维护4棵树状数组,分别维护 \(G,G_i,G_j,G_{ij}\) 就可以求解了。
Code:
int n,m;
struct node{
int t[2100][2100];
void add(int x,int y,int k)
{
for(int i=x;i<=n;i+=lowbit(i))
for(int j=y;j<=m;j+=lowbit(j))
t[i][j]+=k;
}
int asksum(int x,int y)
{
int rt=0;
for(int i=x;i;i-=lowbit(i))
for(int j=y;j;j-=lowbit(j))
rt+=t[i][j];
return rt;
}
}t,ti,tj,tij;
inline void jia(int x,int y,int k){
t.add(x,y,k); ti.add(x,y,k*x);
tj.add(x,y,k*y); tij.add(x,y,k*x*y);
}
inline int qwq(int x,int y)
{
return (t.asksum(x,y)*(x*y+x+y+1)
-tj.asksum(x,y)*(x+1)
-ti.asksum(x,y)*(y+1)
+tij.asksum(x,y));
}
inline void ADD(int x,int y,int xx,int yy,int k){
jia(x,y,k); jia(x,yy+1,-k);
jia(xx+1,y,-k); jia(xx+1,yy+1,k);
}
inline int SUM(int x,int y,int xx,int yy){
return qwq(xx,yy)-qwq(xx,y-1)-qwq(x-1,yy)+qwq(x-1,y-1);
}
…………
………………
main()
{
…………………
ADD(x,y,xx,yy,k);
SUM(x,y,xx,yy);
}
相关题目:
这道题目你要是非要用别的方法也不是不彳亍,就是麻烦的要死。
树状数组上二分
首先,先明确它可以解决什么问题:
$ n $ 个数,要求支持:
- 单点修改。
- 给定 $ t $ ,求一个最大的下标 $ m $ ,使得 $ 1-m $ 的前缀和 $ <= t$。
或者:
- 单点修改或插入新的数。
- 全局第k大(小)
其实就是可以快速的解决动态区间的可以用普通二分解决的问题。
它的原理你可以类比着倍增来理解,就是对于树状数组上的某一节点 $ i $ ,它记录的信息就是 $ [ i - 2^{lowbit(i)} + 1 \text{,}i ] $ 的和,有点类似于倍增,所以对于每一位来决定是否为 \(1\) 或 \(0\) 。
比如说 $ 6 $ ,它的二进制就是 \(110\),就意味着 $ 6 $ 号节点的信息就是$ [ 6 - 2^{lowbit(6)} + 1 \text{,}6 ] = [ 6 - 2 + 1 \text{,}6 ] = [ 5 \text{,} 6 ] $ 的和。
可以参考下图:

那么就可以从高到低,决定每一个二进制位,然后就好了。
或者可以换一个说法:
就是对于一个二进制数,比如说01101100,在我们决定某第 \(i\) 个二进制位的时候,可以想象成是是否要选取已经选到的位置 \(now\) 到 \(now+2^{i}\) 这一段数。
那么,我们在枚举时,先是第 \(7\) 位,我们选定为 \(1\),就意味着我们向后跳了 $ 2^{7} $ 步,然后又选了第 $ 5 $ 位,就相当于我们又向后跳了 \(2^{5}\) 步,就是相当于又选了 \(2^{7}+1\) 到 \(2^{7}+2^{5}\) 之间的数……然后以此类推……(很像倍增,对吧awa)
(可以自己对着图意会一下awa)
不懂得可以理解一下代码(两种写法):
Code:
int n,_log;
//全局第k小
//_log=log2(n);
int erfen1(int k)//正着,有点类似于倍增,更好理解;
{
int ans=0;
for(int i=_log;i>=0;i--)
if(t[ans+(1<<i)]<=k)
ans+=(1<<i),k-=t[ans+(1<<i)];
return ans;
}
//_log=ceil(log2(n));
int erfen2(int k)//倒着,从最高位决定是0还是1
{
int ans=1<<_log;vc
for(int i=_log-1;i>=0;i--)
if(t[ans-(1<<i)]>=k) ans-=(1<<i);
else k-=t[ans-(1<<i)];
return ans;
}
完整测试版:(树状数组记得是某一个数出现了几次)
#include<bits/stdc++.h>
#define lowbit(x) (x&(-x))
using namespace std;
int n,_log;
int t[100005];
void add(int x,int k)
{
while(x<=n)
{
t[x]+=k;
x+=lowbit(x);
}
}
//全局第k小
//_log=log2(n);
int erfen1(int k)//正着,有点类似于倍增,更好理解;
{
int ans=0;
for(int i=_log;i>=0;i--)
if(t[ans+(1<<i)]<=k)
ans+=(1<<i),k-=t[ans+(1<<i)];
return ans;
}
//_log=ceil(log2(n));
int erfen2(int k)//倒着,从最高位决定是0还是1
{
int ans=1<<_log;
for(int i=_log-1;i>=0;i--)
if(t[ans-(1<<i)]>=k) ans-=(1<<i);
else k-=t[ans-(1<<i)];
return ans;
}
int main()
{
cin>>n;
_log=ceil(log2(n));
while(1)
{
int a,b;
cin>>a>>b;
if(b) add(a,b);
else cout<<erfen2(a)/*erfen1(a)*/<<'\n';
}
return 0;
}
相应题目:
一道有一点高级的“模板”题:


