AC自动机
自动机
前置芝士:
1. (看毛片)
2. (字典树)
一定要学会啊 ,不然你根本看不懂下面的东西
然后,接下来我就默认你会了这两个算法了
正文:
1. 什么是自动机?
AC自动机,是 的简称,该算法在 年产生于贝尔实验室,是著名的多模匹配算法。AC自动机是对字典树算法的一种延伸,是字符串中运用非常广泛的一种算法
所以那些以为学了AC自动机就可以万物AC的OIer可以散了
那么,什么又是“多模匹配”呢?
我们首先引入一个概念:模式串匹配
模式串匹配就是有两个字符串: 和 ,问 里面是否有、有几个,分别在什么位置的子串是 。这样的问题我们称为模式串匹配问题。在这里我们称 为文本串, 为模式串。
那么所谓的“单模匹配”意思就是只有单个模式串在文本串上进行匹配 。
就是
然后,顾名思义,“多模匹配”就是有多个模式串在文本串上进行匹配。
方法就是我们今天的主角:AC自动机
2. 自动机什么原理
首先,对于多模式串匹配,我们会很容易想到一个思路:
不就是跑多次单模匹配吗
所以我们可以跑 次 。
复杂度
好了,暴力想完了,我们来想一想可不可以优化。
首先, 是怎么做到快速匹配的,答案是利用了 数组,即失配后快速跳到已经匹配的位置的后缀和模式串的前缀的最大相同位置。
那么,在多模式串匹配时我们可不可以也这样呢?
答案是可以的。
这就引入了一个概念: 指针(即失配指针)。
指针和 里的 数组功能相似,都是可以实现快速匹配。
我们首先可以通过字典树(Trie树)来记录所有的模式串。
然后 指针指向的位置就是当前匹配到的位置的真后缀在字典树上从根结点开始的真前缀的最大相同位置。
形象化的解释:
(举例子最好了 $ (/ω\) $ )
模式串:his、hers、she
首先,对于模式串建立一颗字典树:
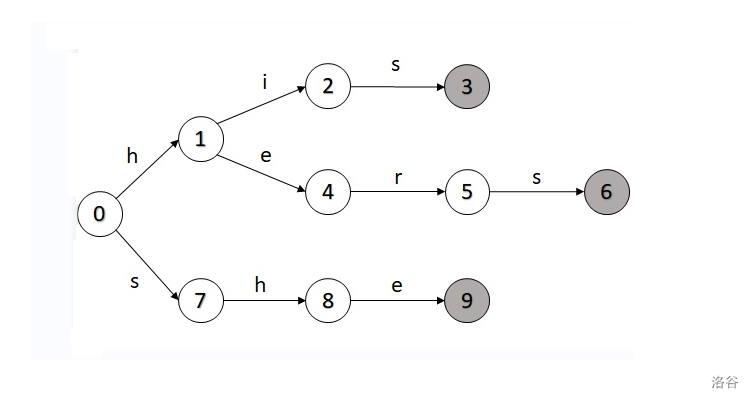
然后,我们可以依次依据以下四条来建立 边:
- 根节点(root) 边指向自己。
- 父亲是根节点(root)则 边指向父亲(root)
- 如果父亲的 边指向的节点可以容纳当前节点(即有指向相同字母的指针所指向的节点),则指向容纳自己的节点所指向的相同字母的节点。
- 假设无法容纳,则跳到父亲节点的 边指向的节点,重复3号过程。(如果指到了根节点(root),则直接指向根节点(root))。
那么我们首先建出 和 :
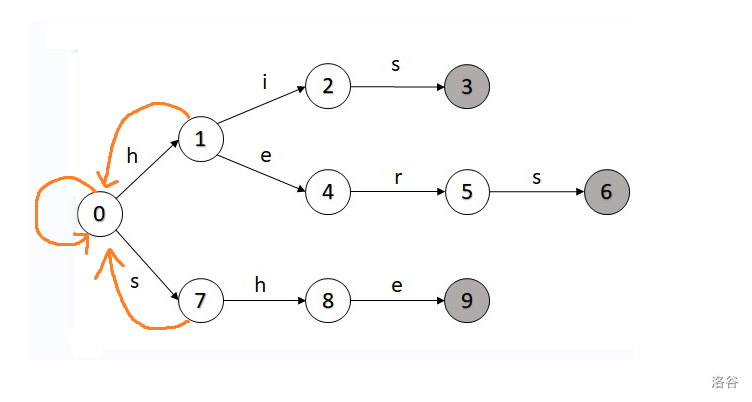
然后,我们以“ ” 为特例来说一下:
对于 号节点,我们看向它父亲的 边指向的节点,即 号(root)节点。
之后发现 有一条“ ”边,所以就将 号节点的 指向 号节点。
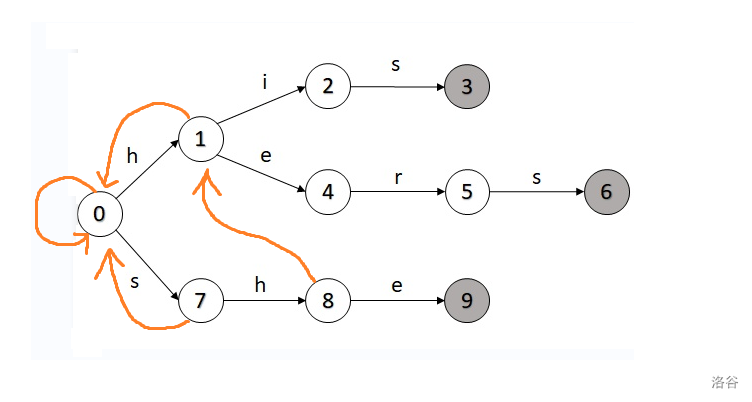
下一层:对于 号节点,我们再按照 和 来建 边:

然后依次类推:
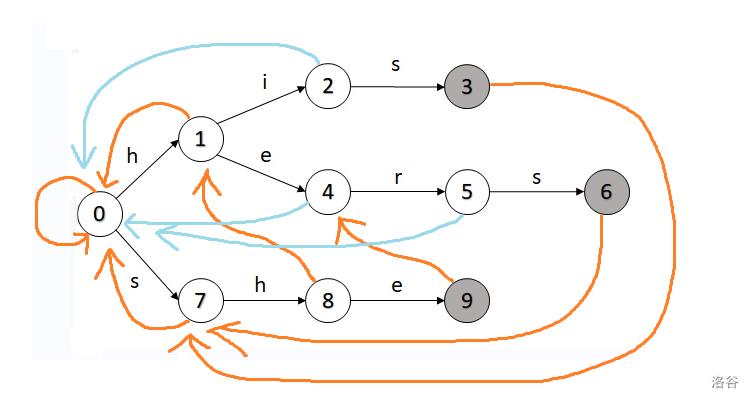
(蓝色的也是 边,但是是无法匹配所以指向根节点的边)
大家可以意会一下,应该还挺好理解的。
所以假设当前无法继续匹配的话,就可以直接跳到 边,就实现了快速匹配。
3. 代码实现:
建立 边一般用的是 ,因为可以用一个很巧妙地方法省去第 条的回溯,并且在查询时还可以十分巧妙的加快 。
先贴一下建边的全代码,一会再分开,在注释里面细细分析:
(如果你觉得太简单,可以直接跳过)
queue<int>q;
void build_fail()
{
for(int i=0;i<26;i++)
if(tr[0].to[i])
q.push(tr[0].to[i]);
while(q.size())
{
int now=q.front();
q.pop();
for(int i=0;i<26;i++)
{
if(tr[now].to[i])
{
tr[tr[now].to[i]].fail=tr[tr[now].fail].to[i];
q.push(tr[now].to[i]);
}
else tr[now].to[i]=tr[tr[now].fail].to[i];
}
}
}
首先,对于父亲就是根节点的点,直接处理,并放入队列中:
for(int i=0;i<26;i++)
if(tr[0].to[i])
q.push(tr[0].to[i]);
之后处理其他的点:
while(q.size())
{
int now=q.front();
q.pop();
for(int i=0;i<26;i++)
{
if(tr[now].to[i])//如果有当前这个点
{
tr[tr[now].to[i]].fail=tr[tr[now].fail].to[i];
//就把这个点的 fail 边指向它父亲的 fail 边
// 指向的点的指向同样字母的点。
//注意,这里不用判断它父亲的 fail 边指向的点
// 可不可以容纳这个点,
// 就是有没有指向这个字母的边。
//这里是最妙的地方(我觉得也是唯一妙的地方(((
// 原因在 else 后面的那一句(解释也在那里)。
q.push(tr[now].to[i]);
//放入队列
}
else tr[now].to[i]=tr[tr[now].fail].to[i];
//这里直接就可以实现回溯的功能。
//因为假设后来某一个点要看当前这个点可不可以容纳 to[i],
//但是事实上是没有这个点,所以我们要回溯,
//要跳到父亲节点的 fail 边指向的节点,
//然后,我们当前记录的就直接是父亲的 fail 的 fail 的 to[i],
//所以就不用回溯了,
//所以上面就不用判断可不可以容纳。
//然后,因为是 BFS ,所以当前点之前的点已经同理的处理完了
//综上,这样子就省去了回溯
}
}
并且,还有一个好的地方。
就是我们在查找的时候,如果有下一位匹配不上的情况,那么我们完全不用管,不用判断可不可以匹配下一位,就直接向下匹配就好了。
因为匹配不上的话,就需要跳到当前的 ,然后可以发现,我们在处理的过程中,如果没有下一位,那 记得就直接是 。
所以,AC自动机讲解完毕 。
4. 例题:
P3808 【模板】AC 自动机(简单版)
真的就是模板,不会写的直接打回去重学(((
#include<bits/stdc++.h>
using namespace std;
inline int read(char s[]){
char g=getchar();int i=1;
while(g<'a'||g>'z') g=getchar();
while(g>='a'&&g<='z') s[i]=g,i++,g=getchar();
return i-1;
}
int n,num;
char s[1000006];
struct node{
int end;
int fail;
int to[26];
}tr[1000006];
void in(char s[],int len)
{
int p=0;
for(int i=1;i<=len;i++)
{
if(!tr[p].to[s[i]-'a']) tr[p].to[s[i]-'a']=++num;
p=tr[p].to[s[i]-'a'];
}
tr[p].end++;
}
int cx(char s[],int len)
{
int ans=0,p=0;
for(int i=1;i<=len;i++)
{
p=tr[p].to[s[i]-'a'];
int now=p;
while(tr[now].end>=0&&now)
{
ans+=tr[now].end;
tr[now].end=-1;
now=tr[now].fail;
}
}
return ans;
}
queue<int>q;
void build_fail()
{
for(int i=0;i<26;i++)
if(tr[0].to[i])
q.push(tr[0].to[i]);
while(q.size())
{
int now=q.front();
q.pop();
for(int i=0;i<26;i++)
{
if(tr[now].to[i])
{
tr[tr[now].to[i]].fail=tr[tr[now].fail].to[i];
q.push(tr[now].to[i]);
}
else tr[now].to[i]=tr[tr[now].fail].to[i];
}
}
}
int main()
{
cin>>n;
for(int i=1;i<=n;i++)
{
int len=read(s);
in(s,len);
}
build_fail();
int len=read(s);
cout<<cx(s,len)<<'\n';
return 0;
}
双倍经验!!!P3796 【模板】AC 自动机(加强版)
不过,这个可不是直接交上一题的代码,是需要稍作修改的 。
还有:
提高一点的,不过还就只是 自动机模板 。



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· TypeScript + Deepseek 打造卜卦网站:技术与玄学的结合
· 阿里巴巴 QwQ-32B真的超越了 DeepSeek R-1吗?
· 如何调用 DeepSeek 的自然语言处理 API 接口并集成到在线客服系统
· 【译】Visual Studio 中新的强大生产力特性
· 2025年我用 Compose 写了一个 Todo App