二维数点
二维数点
很早之前就听说了二维数点,也知道它能干啥,但是一直不知道怎么实现qwq。今天终于学会了awa,赶紧写一篇(lyx /bx/bx/bx
1. 二维数点是什么?
二维数点又称二位偏序,形象化的解释就是在一个二维平面上有许多的点,让你数出在一个区间内,一共有几个点。
就是像这样:
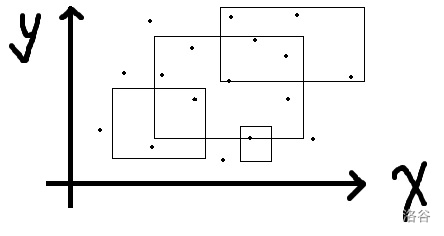
然后问你在这个区间里有多少个点。
(图丑勿喷qwq
2. 二维数点可以干什么?
二维数点通常可以处理类似给你一个序列,让你求出在区间 $ [l,r] $ 里,有多少数在 $ [a,b] $ 之间。
其实就是有两个限制的情况下,让你求出有多少符合要求的元素。
3. 二维数点的问题如何转换+处理?
我们可以发现,二维数点就是二维偏序,所以有很多的解法,比如:扫描线思想+线段树/树状数组,主席树,CDQ分治,K-D Tree(后两个还可以解决更高维的偏序问题)。
然后我用的方法就是 扫描线思想+线段树/树状数组 (当然,因为处理的东西一般比较简单,所以我就直接用常数更小的树状数组了 $ awa $ )
4.二维数点实现:
首先,如果数据范围十分地小,只有 $ 1e4 $ 的话,我们可以用二位前缀和做,但是,二维数点的题目范围一般都很大,大概是 $ 2e5-2e6 $ ,所以二位前缀和不可行。
但是我们可以用一下二位前缀和的思路,将一个我们要询问的矩形:
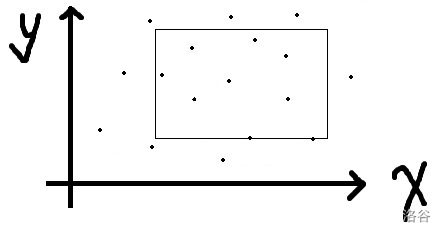
转成这样:
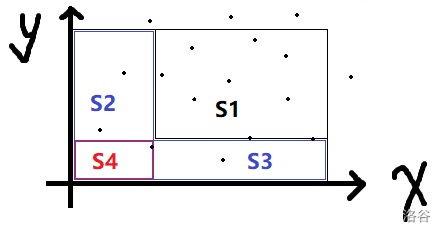
那么原矩形的点的数量其实就等于 S1-S2-S3+S4
(注意:这里的 $ S1 $ 是从 $ (0,0) $ 算的整个矩形。)
所以我们就可以将原矩形一分为四,然后现在问题就变成了求对于一个点 $ (x,y) $ , $ x $ 和 $ y $ 都小于这个点的点一共有多少个 $ awa $
这个其实已经和扫描线十分像了,所以我们可以借鉴一下扫描线的处理方法,套在这类题上就是:
先将一个矩形拆成四个询问,然后对于所有的点按照 $ x $ 为第一关键字, $ y $ 为第二关键字排序,对于一个询问,我们就只记它的右上角,也一起排序(如果有位置相同的点就优先排普通元素)。之后顺序枚举加点。
我们可以发现,当我们枚举到一个询问时,$ x $ 和 $ y $ 都小于这个询问的点都一定已经枚举过了(如图):
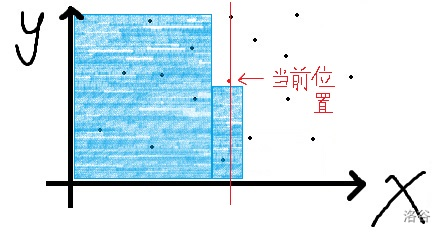
(红色的线是当前所枚举到的点的 $ x $ ,蓝色是已经枚举过的范围)
我们可以把那根红线想象成扫描线的线,发现要处理的东西和扫描线十分的像。
所以我们可以用类似于扫描线的处理方法:
先对点的 $ y $ 坐标离散化一下,然后基于 $ y $ 轴建一棵 树状数组/线段树 来维护区间和。对于枚举到的一个点,将它 $ y $ 轴所对应在 树状数组/线段树 上的点 $ +1 $ 。
因为我们按 $ x $ 排序了,所以所有枚举过的点的 $ x $ 一定小于询问,那么我们就只需要看一下已经枚举过的点 $ y $ 坐标也小于询问的点有多少。
其实就是问 树状数组/线段树 上 $ 0 $ 到询问的 $ y $ 的区间和。
然后统计入答案就好了 $ awa $ 。
几个注意事项:
-
我们是将一个区间分成了四个区间,然后抽象成了一个点(询问区间的右上角),加入点集一起排序,可以更加方便的求解,但是一定注意有普通的点和询问的点重合的情况,一定要在排序时将普通的点排在前面。
-
二维数点只需要维护单点加和区间和,所以直接用树状数组比较好,因为 $ 快♂ awa $ 。主要是二维数点的空间和时间都是 $ O(n+4m) $的(n是点数,m是矩形的数量),如果用线段树就会直接常数爆炸。
然后:
一道模板题:
P2163 [SHOI2007]园丁的烦恼
贴个代码 $ awa $ :
这个已经是最板的题了,如果不会建议重学
#include<bits/stdc++.h>
using namespace std;
inline int read(){
int ans=0; char g=getchar();
while(g<'0'||g>'9'){g=getchar();}
while(g>='0'&&g<='9'){ans=(ans<<3)+(ans<<1)+(g^48);g=getchar();}
return ans;
}
inline void out(long long A){
if(A<0) putchar('-'),A=-A;
if(A>9) out(A/10);
putchar(A%10+'0'); return;
}
int n,m,num,cnt;
int ans[500005];
struct node{
int x,y,bh,ls_y;
bool f,lx;
}a[2500005];
inline bool cmp_x(node A,node B){return A.x==B.x?(A.y==B.y?A.lx<B.lx:A.y<B.y):A.x<B.x;}
inline bool cmp_y(node A,node B){return A.y<B.y;}
int t[2500005];
inline int lowbit(int x){return (x&(-x));}
inline void add(int x)
{
while(x<=cnt)
{
t[x]++;
x+=lowbit(x);
}
}
inline int sum(int x)
{
int ans=0;
while(x)
{
ans+=t[x];
x-=lowbit(x);
}
return ans;
}
int main()
{
n=read(); m=read();
for(int i=1;i<=n;i++)
{
a[++num].x=read();
a[num].y=read();
}
for(int i=1;i<=m;i++)
{
int lu=++num,ld=++num,ru=++num,rd=++num;
a[ld].x=read(); a[ld].y=read(); a[ru].x=read(); a[ru].y=read();
a[ld].x--; a[ld].y--;
a[ld]={a[ld].x,a[ld].y,i,0,1,1};
a[ru]={a[ru].x,a[ru].y,i,0,1,1};
a[lu]={a[ld].x,a[ru].y,i,0,0,1};
a[rd]={a[ru].x,a[ld].y,i,0,0,1};
}
sort(a+1,a+1+num,cmp_y);
a[0].y=-1;
for(int i=1;i<=num;i++)
{
if(a[i].y!=a[i-1].y) a[i].ls_y=++cnt;
else a[i].ls_y=cnt;
}
sort(a+1,a+1+num,cmp_x);
for(int i=1;i<=num;i++)
{
int z=sum(a[i].ls_y);
if(a[i].lx) ans[a[i].bh]+=(a[i].f?z:-z);
else add(a[i].ls_y);
}
for(int i=1;i<=m;i++)
{
out(ans[i]);
puts("");
}
return 0;
}
然后:
双倍经验!!(P3755 [CQOI2017]老C的任务)
题解:把上一道题的代码贴过来,然后多输入一个点权,改成long long,再将树状数组里的“+1”换成“+k”,你就会发现你过了(当然如果你用快读快写了的话还要记得判负号) $ awa $
code:
(大家可以用 $ fc $ 比对一下(((
#include<bits/stdc++.h>
using namespace std;
inline int read(){
int ans=0; bool f=0;char g=getchar();
while(g<'0'||g>'9'){f|=(g=='-');g=getchar();}
while(g>='0'&&g<='9'){ans=(ans<<3)+(ans<<1)+(g^48);g=getchar();}
return (f?-ans:ans);
}
inline long long readl(){
long long ans=0; bool f=0; char g=getchar();
while(g<'0'||g>'9'){f|=(g=='-');g=getchar();}
while(g>='0'&&g<='9'){ans=(ans<<3)+(ans<<1)+(g^48);g=getchar();}
return (f?-ans:ans);
}
inline void out(long long A){
if(A<0) putchar('-'),A=-A;
if(A>9) out(A/10);
putchar(A%10+'0'); return;
}
int n,m,num,cnt;
long long ans[100005];
struct node{
long long z;
int x,y,bh,ls_y;
bool f,lx;
}a[500005];
inline bool cmp_x(node A,node B){return A.x==B.x?(A.y==B.y?A.lx<B.lx:A.y<B.y):A.x<B.x;}
inline bool cmp_y(node A,node B){return A.y<B.y;}
long long t[500005];
inline int lowbit(int x){return (x&(-x));}
inline void add(int x,long long k)
{
while(x<=cnt)
{
t[x]+=k;
x+=lowbit(x);
}
}
inline long long sum(long long x)
{
long long ans=0;
while(x)
{
ans+=t[x];
x-=lowbit(x);
}
return ans;
}
int main()
{
n=read(); m=read();
for(int i=1;i<=n;i++)
{
a[++num].x=read();
a[num].y=read();
a[num].z=readl();
}
for(int i=1;i<=m;i++)
{
int lu=++num,ld=++num,ru=++num,rd=++num;
a[ld].x=read(); a[ld].y=read(); a[ru].x=read(); a[ru].y=read();
a[ld].x--; a[ld].y--;
a[ld]={0,a[ld].x,a[ld].y,i,0,1,1};
a[ru]={0,a[ru].x,a[ru].y,i,0,1,1};
a[lu]={0,a[ld].x,a[ru].y,i,0,0,1};
a[rd]={0,a[ru].x,a[ld].y,i,0,0,1};
}
sort(a+1,a+1+num,cmp_y);
for(int i=1;i<=num;i++)
{
if(a[i].y!=a[i-1].y||i==1) a[i].ls_y=++cnt;
else a[i].ls_y=cnt;
}
sort(a+1,a+1+num,cmp_x);
for(int i=1;i<=num;i++)
{
long long z=sum(a[i].ls_y);
if(a[i].lx) ans[a[i].bh]+=(a[i].f?z:-z);
else add(a[i].ls_y,a[i].z);
}
for(int i=1;i<=m;i++)
{
out(ans[i]);
puts("");
}
return 0;
}


