折半搜索

（今天终于自学了折半搜索，赶紧记一下）

折半搜索：

折半搜索（Meet in the Middle）思路十分的好理解，

折半搜索的主要思想是：
对于一类搜索问题，将本来直接搜索的算法转换成分别搜索两部分，
再把两部分结果组合得到最终答案。
通常这两部分大小相等，但有时候碍于空间或者时间限制，需要微调。

（这是网上的标准解答，但明显不是人话qwq）

（所以我们来翻译一下awa）

折半搜索形象化的解释就是：

走迷宫的游戏大家都玩过吧？awa？如果这个迷宫很简单，或者很小，那我们可以直接“一眼瞪”，发现答案。

但是，如果这个迷宫很大，怎么办qwq？

（我知道！这个我知道！你接下来是不是就想说DFS，或者是BFS的思想awa？）

当然不是（（（

其实这个迷宫如果真的很大，那我们人脑几乎是没有办法去穷举的，但是，我们小时候应该有很多人用过一个小技巧：

从结尾向出发点走，如果结尾出发的路径和从起始点出发的路径接在了一起，那么就是答案了\(awa\)

对！这就是折半搜索。\(awa\)

是不是很简单awa

再来一张图方便大家理解（本来想自己画，但是发现自己画的烂的一匹，不如从网上找一张 $ qwq $ ）：

假如有一个状态，让你从上面的红点转移到下面的红点

如果你从上面的点搜完整个图，就会有许多的浪费导致复杂度十分的高

如果图是一个二叉树，那这样的搜索的复杂度就会达到 $ O(2^{N+1}) $

图都已经贺了，就懒得改成二叉树了\(QAQ\)，大家感性理解一下\(awa\)

但是，如果你像这样：

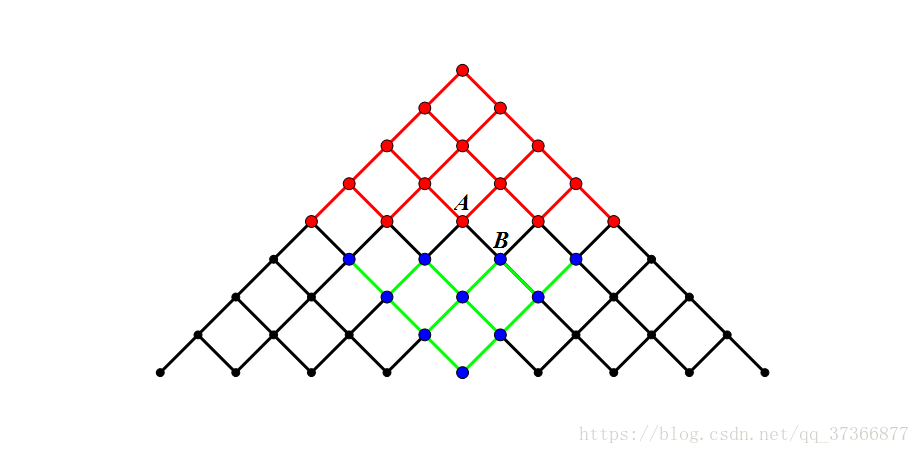
分别从下面和上面各搜一半，你会发现：

时间复杂度指数降了一半！！

**降到了 $ O(2^{n/2+1}+k) $ **

K 是将两个状态综合在一起求出答案的时间复杂度，一般不超过 $ O(2^{n/2+1} \times logN) $

所以折半搜索十分快（相对于 DFS 和 BFS ）$ awa $。

然后同时你会发现，状态数的指数也少了一半

因为要跑的状态少了一半,所以空间上折半搜索也十分优秀 $ awa $

相关题目：

那么，下面我们来一道模板题：

洛谷P4799 世界冰球锦标赛

这就是一道模板题，直接搜索是会超时的，还会超空间

但是折半搜索直接将他的时间和空间降了一半的指数

所以就过了awa：

Code：

#include<bits/stdc++.h>
using namespace std;
long long n,m,a[45],ans;
long long ans1[(1<<21)],num1;
long long ans2[(1<<21)],num2;
void dfs(long long aa[],long long now,long long nn,long long sum,long long &num)
{
	if(sum>m)	return;
	if(now>nn)
	{
		aa[++num]=sum;
		return;
	}
	dfs(aa,now+1,nn,sum+a[now],num);
	dfs(aa,now+1,nn,sum,num);
}
int main()
{
	cin>>n>>m;
	for(int i=1;i<=n;i++)	cin>>a[i];
	dfs(ans1,1,n/2,0,num1);
	dfs(ans2,n/2+1,n,0,num2);
	sort(ans1+1,ans1+1+num1);
	sort(ans2+1,ans2+1+num2);
	for(int i=1;i<=num1;i++)
		ans+=upper_bound(ans2+1,ans2+1+num2,m-ans1[i])-ans2-1;
	cout<<ans<<'\n';
	return 0;
}

然后，一道好题：

洛谷P3067

The End