RANSAC直线拟合,并与最小二乘法结果进行对比
RANSAC直线拟合,并与最小二乘法结果进行对比
1 //===================================================================// 2 //Program:RANSAC直线拟合,并与最小二乘法结果进行对比 3 //Data:2024.8.16 4 //Author:yuan jiakai 5 //Version:V1.0 6 //====================================================================// 7 #include <iostream> 8 #include <opencv2/opencv.hpp> 9 10 11 //RANSAC 拟合2D 直线 12 //输入参数:points--输入点集 13 // iterations--迭代次数 14 // sigma--数据和模型之间可接受的差值,车道线像素宽带一般为10左右 15 // (Parameter use to compute the fitting score) 16 // k_min/k_max--拟合的直线斜率的取值范围. 17 // 考虑到左右车道线在图像中的斜率位于一定范围内, 18 // 添加此参数,同时可以避免检测垂线和水*线 19 //输出参数:line--拟合的直线参数,It is a vector of 4 floats 20 // (vx, vy, x0, y0) where (vx, vy) is a normalized 21 // vector collinear to the line and (x0, y0) is some 22 // point on the line. 23 //返回值:无 24 void fitLineRansac(const std::vector<cv::Point2f>& points, 25 cv::Vec4f &line, 26 int iterations = 1000, 27 double sigma = 1., 28 double k_min = -7., 29 double k_max = 7.) 30 { 31 unsigned int n = points.size(); 32 33 if(n<2) 34 { 35 return; 36 } 37 38 cv::RNG rng; 39 double bestScore = -1.; 40 for(int k=0; k<iterations; k++) 41 { 42 int i1=0, i2=0; 43 while(i1==i2) 44 { 45 i1 = rng(n); 46 i2 = rng(n); 47 } 48 const cv::Point2f& p1 = points[i1]; 49 const cv::Point2f& p2 = points[i2]; 50 51 cv::Point2f dp = p2-p1;//直线的方向向量 52 dp *= 1./norm(dp); 53 double score = 0; 54 55 if(dp.y/dp.x<=k_max && dp.y/dp.x>=k_min ) 56 { 57 for(int i=0; i<n; i++) 58 { 59 cv::Point2f v = points[i]-p1; 60 double d = v.y*dp.x - v.x*dp.y;//向量a与b叉乘/向量b的摸.||b||=1./norm(dp) 61 //score += exp(-0.5*d*d/(sigma*sigma));//误差定义方式的一种 62 if( fabs(d)<sigma ) 63 score += 1; 64 } 65 } 66 if(score > bestScore) 67 { 68 line = cv::Vec4f(dp.x, dp.y, p1.x, p1.y); 69 bestScore = score; 70 } 71 } 72 } 73 74 int main() 75 { 76 cv::Mat image(720,1280,CV_8UC3,cv::Scalar(125,125,125)); 77 78 //以车道线参数为(0.7657,-0.6432,534,548)生成一系列点 79 double k = -0.6432/0.7657; 80 double b = 548 - k*534; 81 82 std::vector<cv::Point2f> points; 83 84 for (int i = 360; i < 720; i+=10) 85 { 86 cv::Point2f point(int((i-b)/k),i); 87 points.emplace_back(point); 88 } 89 90 //加入直线的随机噪声 91 cv::RNG rng((unsigned)time(NULL)); 92 for (int i = 360; i < 720; i+=10) 93 { 94 int x = int((i-b)/k); 95 x = rng.uniform(x-10,x+10); 96 int y = i; 97 y = rng.uniform(y-30,y+30); 98 cv::Point2f point(x,y); 99 points.emplace_back(point); 100 } 101 102 //加入噪声 103 for (int i = 0; i < 720; i+=20) 104 { 105 int x = rng.uniform(1,640); 106 int y = rng.uniform(1,360); 107 108 cv::Point2f point(x,y); 109 points.emplace_back(point); 110 } 111 112 113 114 115 116 int n = points.size(); 117 for (int j = 0; j < n; ++j) 118 { 119 cv::circle(image,points[j],5,cv::Scalar(0,0,0),-1); 120 } 121 122 123 //RANSAC 拟合 124 if(1) 125 { 126 cv::Vec4f lineParam; 127 fitLineRansac(points,lineParam,1000,10); 128 double k = lineParam[1] / lineParam[0]; 129 double b = lineParam[3] - k*lineParam[2]; 130 131 cv::Point p1,p2; 132 p1.y = 720; 133 p1.x = ( p1.y - b) / k; 134 135 p2.y = 360; 136 p2.x = (p2.y-b) / k; 137 138 cv::line(image,p1,p2,cv::Scalar(0,255,0),2); 139 } 140 141 142 //最小二乘法拟合 143 if(1) 144 { 145 cv::Vec4f lineParam; 146 cv::fitLine(points,lineParam,cv::DIST_L2,0,0.01,0.01); 147 double k = lineParam[1] / lineParam[0]; 148 double b = lineParam[3] - k*lineParam[2]; 149 150 cv::Point p1,p2; 151 p1.y = 720; 152 p1.x = ( p1.y - b) / k; 153 154 p2.y = 360; 155 p2.x = (p2.y-b) / k; 156 157 cv::line(image,p1,p2,cv::Scalar(0,0,255),2); 158 } 159 160 161 162 163 cv::imshow("image",image); 164 cv::waitKey(0); 165 166 return 0; 167 }
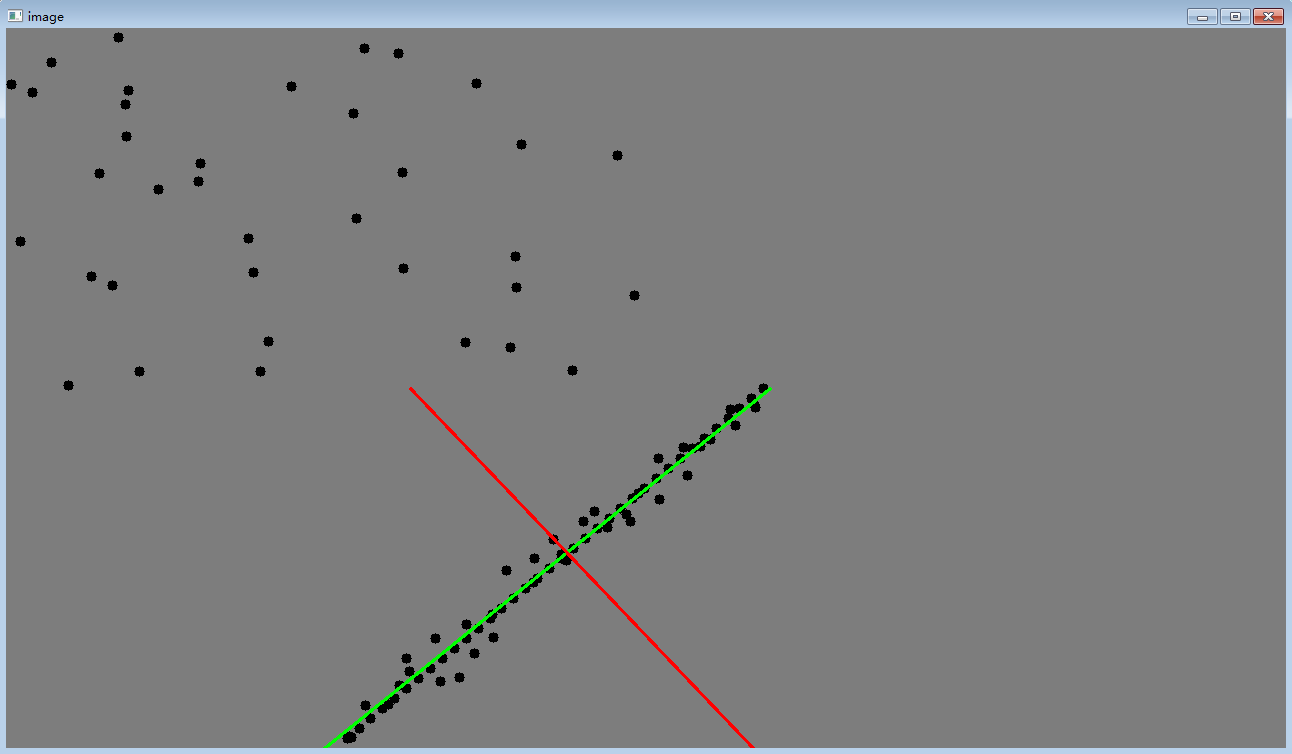
RANSAC优缺点:
RANSAC的优点是它能鲁棒的估计模型参数。例如,它能从包含大量局外点的数据集中估计出高精度的参数。
RANSAC的缺点是它计算参数的迭代次数没有上限;如果设置迭代次数的上限,得到的结果可能不是最优的结果,甚至可能得到错误的结果。RANSAC只有一定的概率得到可信的模型,概率与迭代次数成正比。RANSAC的另一个缺点是它要求设置跟问题相关的阀值。
RANSAC只能从特定的数据集中估计出一个模型,如果存在两个(或多个)模型,RANSAC不能找到别的模型。
RANSAC可以对局外点进行剔除,这一点是比较好的,但它也并不是完美的,当它对于拟合两条**似*行直线分布的点时,拟合出来的结果并不是最好的,甚至可以说拟合的结果是不对的。因为最终的正确结果有可能并不是经过所给的数据点的,如下图所示:






