单应性矩阵与相机内外参之间的关系

                                   单应性矩阵与相机内外参之间的关系

标定：已知世界坐标系平面内的三维坐标和像素坐标，求解内参和外参；

本质矩阵和基本矩阵：已知内参和两幅图像中对应点的坐标，通过对极约束（八点法，尺度等价性，齐次坐标）求解相机的运动R和t（用到RANSAC）；

单应矩阵：根据同一平面上的点在不同图像上的坐标，得到对应的变换关系（十四讲）；

PNP：根据三维空间点的坐标和他们的投影坐标（归一化平面坐标），估计相机的位姿（用到BA）；

ICP：得到三维点云的变换关系（使用SVD）；

尺度等价性：

                                           

一、Slam十四讲

相机模型（针孔相机模型）

 

                                    

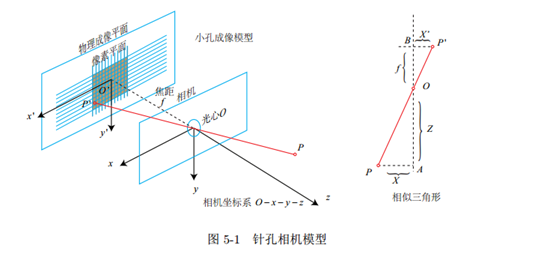
注意：相机坐标系和成像平面；把成像平面对称到相机前方，去掉负号；

                                        

像素坐标系的定义:

                                          

 像素坐标（分辨率作为比例系数，以左上角作为原点就要加上偏移量），

 内参数矩阵（分辨率和偏移量）

  P是点在相机坐标系中的坐标；

                                         

Pw是点在世界坐标系中的坐标；需要使用一个刚体变换（外参）；

使用齐次坐标来描述；

将相机坐标系中的坐标归一化到归一化平面

                                     

                                     

             标定原理:【】OPENCV立体标定  ,二代标定原理

二、单应矩阵H的求解（最小奇异值的特征向量）（参考二代标定原理）

 

因为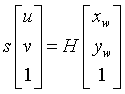，根据牙齿二代参考的浙大论文，可以采用最小平方差方法来计算单应性矩阵H的值。

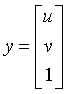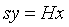令，，则有，所以向量y与向量Hx平行，所以有 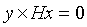（3）成立（叉乘）。

将H用行向量表示成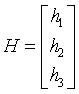，所以（3）可以化为，

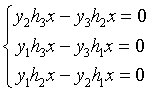又该式子中只有两个是线性无关的，该式可进一步化为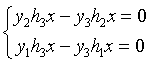 （4）

将（4）式转置可得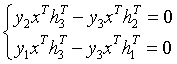，并改写成矩阵运算形式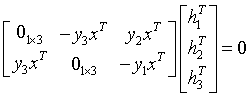： （5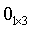）， 表示矩阵[0 0 0]；

 

对于标定板上每个方格的角点，都有上面的两个等式成立，因此有n个点时，可以建立n个类似（5）的方程组，合并这n个方程组，可得

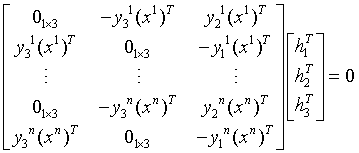                                                                                                              （6）

这样，求解H的问题就变成了求解次线性方程组（6）的问题，利用奇异值分解即可求出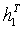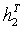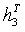，，的值，则H得解。

具体解法：

                                                                        解 Ax = 0

                                                                         

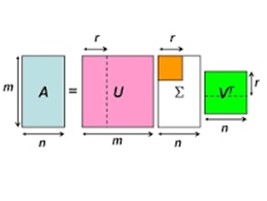
已知: 已知 A∈Rm×n,m≥nA∈Rm×n,m≥n
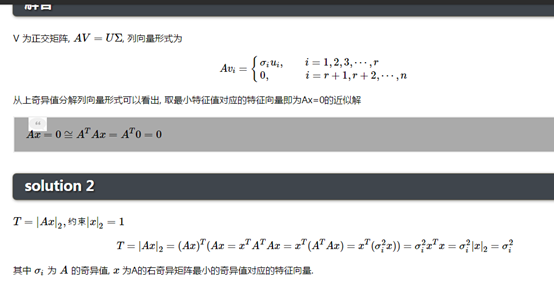
问题: Ax=0Ax=0 的解
求解: 解为A的右奇异矩阵V的最后一列, 即 ATAATA 最小特征值对应的特征向量（参考：线性代数及其应用：二次型：定理6）

                               

 

三、公式推导:

 

相机模型中一般要用到三个坐标系：成像平面参考坐标系、相机参考坐标系和世界坐标系。

1.世界坐标系：

       是在物体（标定板）环境中选择的一个基准坐标系，二代采用的张正友标定方法都以标定板的方格角点为原点，方格的两边为x、y轴，垂直于标定板为z轴建立直角坐标系。度量单位为mm。

2.相机参考坐标系：

       以相机的光心为原点，平行于图像平面的两条垂直边界的方向为x、y轴，相机主光轴为z轴建立三维直角坐标系。度量单位为mm。

3.成像平面参考坐标系：

       以图像平面的主点为原点（主光轴与图像平面交点），建立图像平面的两条垂直边界为x、y轴建立二维直角坐标系。度量单位为像素。

       设世界坐标系中标定板上的一点M的坐标为，它在相机参考坐标系中的坐标为，则它们之间的转换关系为

                                                                                             ，

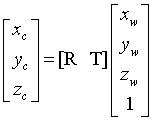R是一个3X3的正交矩阵，表示两个坐标系之间的旋转关系，T为一个3X1矩阵，表示两个坐标系之间的平移关系。

由于R是正交矩阵，因此组成R的9个数中只有三个参数独立，而组成T的三个数则都独立。由于[R T]矩阵只与摄像机相对于物体的位置有关，

因此[R T]称为摄像机的外参矩阵，[R T]的六个独立参数称为摄像机的外参。

设点M以摄像机光心为投影中心，在成像平面参考坐标系上投影点的坐标为，则由相机参考坐标系投影到成像平面参考坐标系之间的转换关系为:

                                                                                    ，

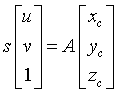s为放缩因子，A是一个3X3矩阵:

                                                                              

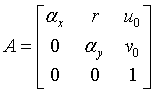
共有5个未知参数，因为这五个参数均只与摄像机的参数有关，称为摄像机的内参矩阵。所以由世界坐标系到成像平面参考坐标系的变换关系可以表示为：

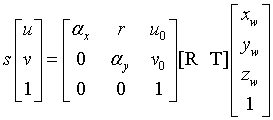                                                                                                              即

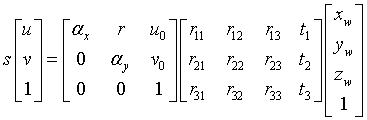                                                                                          （1）

，由于标定板所有点都在z=0的平面上，所以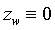，所以（1）式又可以写成

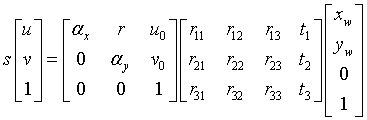                                                                                   ，化简得

 

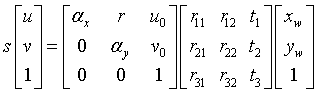                                                                                                     （2）

记

                                                            

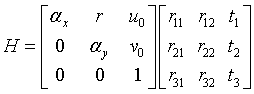
则H为一个3X3矩阵，称为单应矩阵。

 

四、摄像机内参的求解

依据：旋转矩阵的列向量正交,在已知H以后就可以由

                                                             

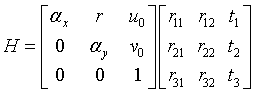
求解摄像机的内外参了。将左式写成

                                                             

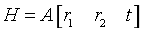
的形式，将A变换到式子左边，可得

                                                            

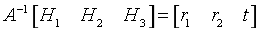
即

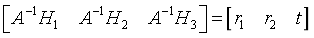                                                                                              （7）

，因为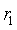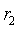，是正交矩阵R的列向量，即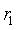与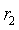是单位正交向量，所以有下式成立：

                                                        ，

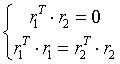代入（7）式可得

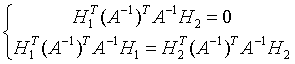                                                                                                   （8）

，令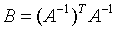，因为B是对称矩阵，所以只有

                                                      

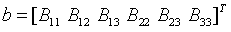
六个数是独立的，类比矩阵二次型，可以知道

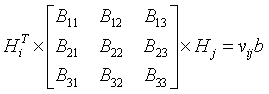                                                                                                        （9）

其中

                                    

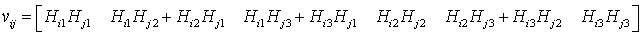
所以利用（9）式，可以将（8）式表示为:

                                                                                           

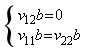
，化成矩阵形式

                                                                                                                                         （10）

由于（10）式中b有6个未知数，而该式只相当于两个方程，所以需要三组不同位置求解出的H，获得3个类似（10）的式子并联立，就能求解出b。

（因为b中的六个未知数由摄像机内参决定，与摄像机位置无关，所以可以利用三个不同位置拍摄标定板，并求解出三个H来求b）。求出b以后就可以得到B，

因为

                                                                               ，

                                                                         

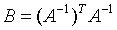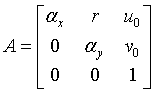
，设B的第i行第j列为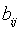，则A的五个未知数可以表示为:

                                                                          

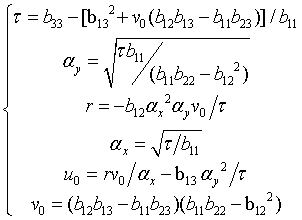
即摄像机内参得解。

五、摄像机外参的求解

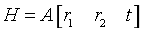                                                                                                   可得:

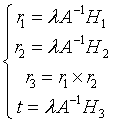                                                                                                         其中

                                                                     

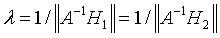
（乘以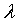的原因：因为前面解得的H是利用向量y与向量Hx平行的条件，即:

                                                                                

 ，这里求解出的H只是被y与向量Hx平行这个条件约束，若H乘上一个常数，它仍然满足这个约束条件，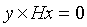

仍成立，因此求解出的H应该是真实的H乘上一个常数比例因子K，1.4中利用H求解内参时k可以被约掉不影响结果，而这里由于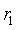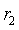，都是单位向量，

所以由

                                                                             

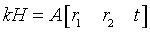
可知     

                                                                        

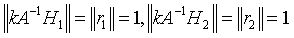
所以

                                                                        

 

                                       

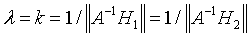
六、求解H的SVD解释

                                            

                                       https://www.cnblogs.com/nowgood/p/jie-ax--0.html 

七、opencv实现

 

                                                        

                                                       

                                                        

                                                       

                                                       

                                                       

                                                       

 

 

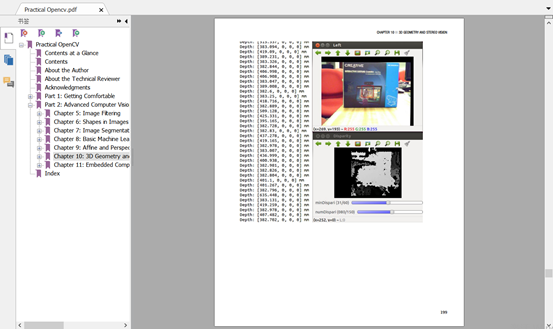
八、POSIT算法

以下来自《学习opencv》

                                         

                                                       

                                                     

                                                     

                                                     

                                                     

                                                    

 

 

九、RANSAC算法

随机采样一致性，用于

                                                  、

博客转自：https://www.cnblogs.com/tangyuanjie/p/14028224.html