opencv常用矩阵操作（加、减、乘、逆、均值、标准差）

OpenCV中的矩阵操作非常重要，本文总结了矩阵的创建、初始化以及基本矩阵操作主要内容包括：

• 创建与初始化
• 矩阵加减法
• 矩阵乘法
• 矩阵转置
• 矩阵求逆
• 矩阵非零元素个数
• 矩阵均值与标准差
• 矩阵全局极值及位置
• 其他矩阵运算函数列表

1. 创建与初始化矩阵

1.1 数据类型

建立矩阵必须要指定矩阵存储的数据类型，图像处理中常用的几种数据类型如下：

CV_8UC1// 8位无符号单通道
CV_8UC3// 8位无符号3通道
CV_8UC4
CV_32FC1// 32位浮点型单通道
CV_32FC3// 32位浮点型3通道
CV_32FC4

包括数据位深度8位、32位，数据类型U:uchar、F:float型以及通道数C1：单通道、C3：三通道、C4：四通道。

1.2 基本方法

我们可以通过载入图像来创建Mat类型矩阵，当然也可以直接手动创建矩阵，基本方法是指定矩阵尺寸和数据类型：

// 基本方法
    cv::Mat a(cv::Size(5,5),CV_8UC1); // 单通道
    cv::Mat b = cv::Mat(cv::Size(5,5),CV_8UC3); //3通道每个矩阵元素包含3个uchar值
    cout<<"a  = "<<endl<<a<<endl<<endl;
    cout<<"b  = "<<endl<<b<<endl<<endl;
    system("pause");

运行结果：

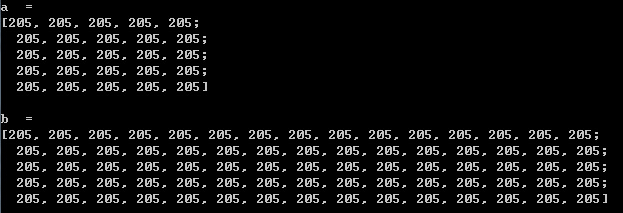
3通道矩阵中，一个矩阵元素包含3个变量。

1.3 初始化方法

上述方法不初始化矩阵数据，因此将出现随机值。如果想避免这种情况，可使用Mat类的几种初始化创建矩阵的方法：

// 初始化方法
    cv::Mat mz = cv::Mat::zeros(cv::Size(5,5),CV_8UC1); // 全零矩阵
    cv::Mat mo = cv::Mat::ones(cv::Size(5,5),CV_8UC1);  // 全1矩阵
    cv::Mat me = cv::Mat::eye(cv::Size(5,5),CV_32FC1);  // 对角线为1的对角矩阵
    cout<<"mz = "<<endl<<mz<<endl<<endl;
    cout<<"mo = "<<endl<<mo<<endl<<endl;
    cout<<"me = "<<endl<<me<<endl<<endl;

运行结果：

2. 矩阵运算

2.1 基本概念

 OpenCV的Mat类允许所有的矩阵运算。 

2.2 矩阵加减法

我们可以使用"+"和"-"符号进行矩阵加减运算。

cv::Mat a= Mat::eye(Size(3,2), CV_32F);
cv::Mat b= Mat::ones(Size(3,2), CV_32F);
cv::Mat c= a+b;
cv::Mat d= a-b;

 

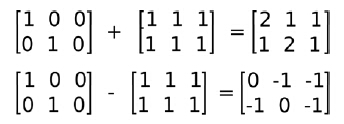
2.3 矩阵乘法

使用"*"号计算矩阵与标量相乘，矩阵与矩阵相乘（必须满足矩阵相乘的行列数对应规则）

    Mat m1= Mat::eye(2,3, CV_32F); //使用cv命名空间可省略cv::前缀，下同
    Mat m2= Mat::ones(3,2, CV_32F);
    cout<<"m1  = "<<endl<<m1<<endl<<endl;
    cout<<"m2  = "<<endl<<m2<<endl<<endl;
    // Scalar by matrix
    cout << "\nm1.*2 = \n" << m1*2 << endl;
    // matrix per element multiplication
    cout << "\n(m1+2).*(m1+3) = \n" << (m1+1).mul(m1+3) << endl;
    // Matrix multiplication
    cout << "\nm1*m2 = \n" << m1*m2 << endl;

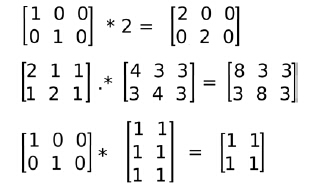
2.4 矩阵转置

矩阵转置是将矩阵的行与列顺序对调（第i行转变为第i列）形成一个新的矩阵。OpenCV通过Mat类的t()函数实现。

// 转置
    Mat m1= Mat::eye(2,3, CV_32F);    
    Mat m1t = m1.t();
    cout<<"m1  = "<<endl<<m1<<endl<<endl;
    cout<<"m1t  = "<<endl<<m1t<<endl<<endl;
    system("pause");

运行结果：

2.5 求逆矩阵

逆矩阵在某些算法中经常出现，在OpenCV中通过Mat类的inv()方法实现

// 求逆
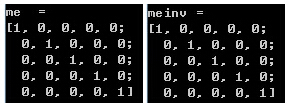
    Mat meinv = me.inv();
    cout<<"me  = "<<endl<<me<<endl<<endl;
    cout<<"meinv = "<<endl<<meinv<<endl<<endl;
    system("pause");

运行结果：

单位矩阵的逆就是其本身。

2.6 计算矩阵非零元素个数

计算物体的像素或面积常需要用到计算矩阵中的非零元素个数，OpenCV中使用countNonZero()函数实现

// 非零元素个数
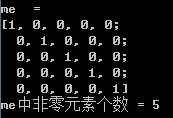
    int nonZerosNum = countNonZero(me); // me为输入矩阵或图像
    cout<<"me  = "<<endl<<me<<endl;
    cout<<"me中非零元素个数 = "<<nonZerosNum<<endl<<endl;
    system("pause");

运行结果：

2.7 均值和标准差

OpenCV提供了矩阵均值和标准差计算功能，可以使用meanStdDev(src,mean,stddev)函数实现。

参数

• src – 输入矩阵或图像
• mean – 均值，OutputArray
• stddev – 标准差，OutputArray

// 均值方差
    Mat mean;
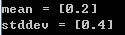
    Mat stddev;
    meanStdDev(me, mean, stddev); //me为前文定义的5×5对角阵
    cout<<"mean = "<<mean<<endl;
    cout<<"stddev = "<<stddev<<endl;
    system("pause");

运行结果：

需要说明的是，如果src是多通道图像或多维矩阵，则函数分别计算不同通道的均值与标准差，因此返回值mean和stddev为对应维度的向量。

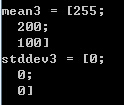
    Mat mean3;
    Mat stddev3;
    Mat m3(cv::Size(5,5),CV_8UC3,Scalar(255,200,100));
    cout<<"m3  = "<<endl<<m3<<endl<<endl;
    meanStdDev(m3, mean3, stddev3);
    cout<<"mean3 = "<<mean3<<endl;
    cout<<"stddev3 = "<<stddev3<<endl;
    system("pause");

多通道矩阵运算结果：

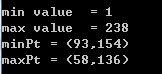
2.8 求最大最小值

求输入矩阵的全局最大最小值及其位置，可使用函数：

void minMaxLoc(InputArray src, CV_OUT double* minVal,
                           CV_OUT double* maxVal=0, CV_OUT Point* minLoc=0,
                           CV_OUT Point* maxLoc=0, InputArray mask=noArray());

参数：

src – 输入单通道矩阵（图像）.
minVal – 指向最小值的指针， 如果未指定则使用NULL
maxVal – 指向最大值的指针， 如果未指定则使用NULL
minLoc – 指向最小值位置（2维情况）的指针， 如果未指定则使用NULL
maxLoc – 指向最大值位置（2维情况）的指针， 如果未指定则使用NULL
mask – 可选的蒙版，用于选择待处理子区域

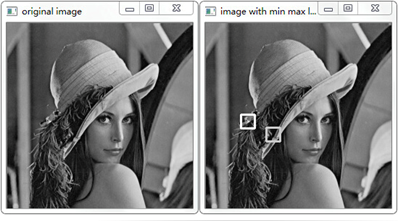
// 求极值 最大、最小值及其位置
    Mat img = imread("Lena.jpg",0);
    imshow("original image",img);
 
    double minVal=0,maxVal=0;
    cv::Point minPt, maxPt;
    minMaxLoc(img,&minVal,&maxVal,&minPt,&maxPt);
    cout<<"min value  = "<<minVal<<endl;
    cout<<"max value  = "<<maxVal<<endl;
    cout<<"minPt = ("<<minPt.x<<","<<minPt.y<<")"<<endl;
    cout<<"maxPt = ("<<maxPt.x<<","<<maxPt.y<<")"<<endl;
    cout<<endl;
 
    cv::Rect rectMin(minPt.x-10,minPt.y-10,20,20);
    cv::Rect rectMax(maxPt.x-10,maxPt.y-10,20,20);
 
    cv::rectangle(img,rectMin,cv::Scalar(200),2);
    cv::rectangle(img,rectMax,cv::Scalar(255),2);
 
    imshow("image with min max location",img);
    cv::waitKey();

运行结果：

输入图像及其最大最小值位置

其他矩阵运算函数见：https://blog.csdn.net/iracer/article/details/51296631

转载于：https://blog.csdn.net/iracer/article/details/51296631