分层图最短路

分层图

分层图确实是个不难的东西我也确实是一个菜鸡...

简要介绍

分层图常在图论问题中出现可任选K条边更改边权（变为0或是原来一半等）时应用。

分层图，就是在应对这种问题时，把原图复制K层（总共K+1层）

每相邻层之间用更改边权后的边连接对应的点（代表进行一次操作）

然后就可以在这个新图中处理，得到问题的最优解

图例如下

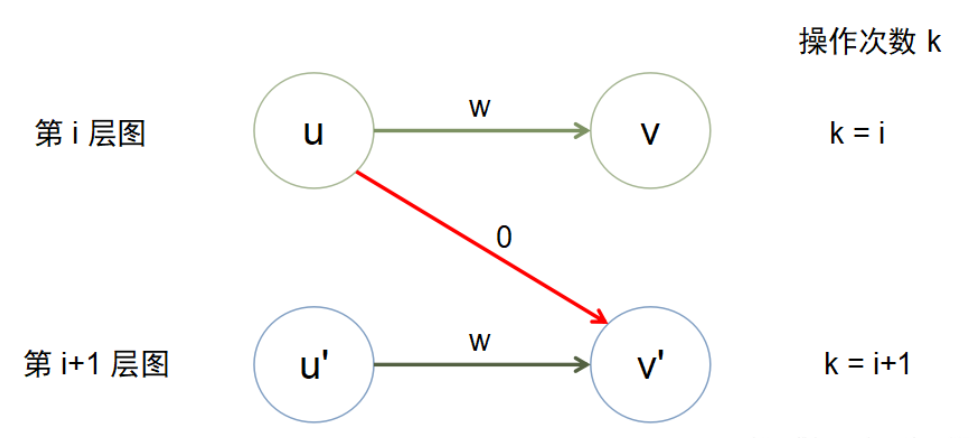
因为连接两层的边代表的是进行了一次不可逆的边权操作，所以都是有向边

每层图内部的边就是和原图一样了

简单说明

可能有人会有疑问，把图复制K层后，空间和时间不会爆炸嘛？

虽然分层图总共有K+1层图

但因为每层都只是单纯的复制原图

所以内容都是一样的，一般没有必要新建图

我们只需要用一个二维数组表示点编号及其所在层数

例如在求最短路时，用 dis[x][k] 表示分层图中在k层的x点的最短距离

即原图中进行了k次边权操作的 x 点最短距离

这样就不需要新建图了

（如果最后还是炸了，说明正解大概不是分层图）

 

例题

题目描述

Your are given an undirect connected graph.Every edge has a cost to pass.You should choose a path from S to T and you need to pay for all the edges in your path. However, you can choose at most k edges in the graph and change their costs to zero in the beginning. Please answer the minimal total cost you need to pay.

您将获得一个无向连通图。每条边都有成本要通过。您应该选择一条从S到T的路径，并且需要为路径中的所有边付费。但是，您可以在图中选择最多k个边，并在开始时将其成本更改为零。请回答您需要支付的最低总费用。（机翻）

输入描述:

The first line contains five integers n,m,S,T,K.
For each of the following m lines, there are three integers a,b,l, meaning there is an edge that costs l between a and b.
n is the number of nodes and m is the number of edges.
第一行包含五个整数n，m，S，T，K。 
对于以下m行中的每一行，有三个整数a，b，l，这意味着在a和b之间存在成本为l的边。 
n是节点数，m是边数。

输出描述:

An integer meaning the minimal total cost.
一个整数表示最小总成本。

示例1

输入

3 2 1 3 1
1 2 1
2 3 2

输出

1

备注:

1≤n,m≤1e3,1≤S,T,a,b≤n,0≤k≤m,1≤l≤1e6
Multiple edges and self loops are allowed.
来源：牛客网暑期多校第四场J题

#include <iostream>
#include <cstdio>
#include <cstring>
#include <string>
#include <queue>
using namespace std;
#define M 1000100
struct node {
    int to,next,w;
}e[2*M];
typedef pair <int,int> p;
priority_queue <p,vector<p>,greater<p> > q; 
int dis[1010][1010],head[M],s,t,n,m,k=0;
int path[1010],cnt;
bool vis[1010][1010];
void add(int u,int v,int w) {
    e[k].to=v; e[k].next=head[u]; 
    e[k].w = w; head[u]=k++;
}
void dij() {
    for (int i=1;i<=n;i++) {
        for (int j=0;j<=k;j++)
            dis[i][j] = 0x7f7f7f7f;
    }
    memset(vis,0,sizeof vis);
    int now,son,x;
    dis[s][0] = 0;
    q.push(make_pair(0,s));
    while ( q.size() ) {
        now = q.top().second;
        q.pop();
        if ( now%n == 0 ) 
            x = now/n-1,now=n;
        else x=now/n,now%=n;
        if ( vis[now][x] ) continue;
        vis[now][x] = 1;
        for (int i=head[now];~i;i=e[i].next) {
            son = e[i].to;
            if ( dis[now][x]+e[i].w<dis[son][x]) {
                dis[son][x] = dis[now][x]+e[i].w;
                q.push(make_pair(dis[son][x],son+n*x));
            }
            if ( x != cnt ) {
                if ( dis[son][x+1] > dis[now][x]) {
                    dis[son][x+1] = dis[now][x];
                    q.push(make_pair(dis[son][x+1],son+x*n+n));
                }
            }
        }
    }
}
int main() {
    int a,b,c;
    memset(head,-1,sizeof head);
    scanf("%d%d%d%d%d",&n,&m,&s,&t,&cnt);
    for (int i=1;i<=m;i++) {
        scanf("%d%d%d",&a,&b,&c);
        add(a,b,c);
        add(b,a,c);
    }
    dij();
    printf("%d\n",dis[t][cnt]);
    return 0;
}