[CQOI2018] 解锁屏幕
题目背景
使用过Android 手机的同学一定对手势解锁屏幕不陌生。Android 的解锁屏幕由3X3 个点组成，手指在屏幕上画一条线，将其中一些点连接起来，即可构成一个解锁图案。如下面三个例子所示:
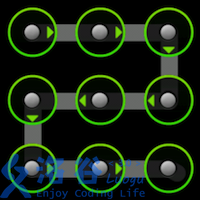
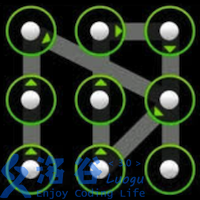
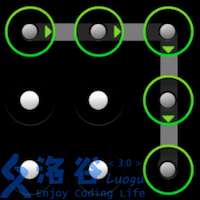
题目描述
画线时还需要遵循一些规则:
-
连接的点数不能少于4 个。也就是说只连接两个点或者三个点会提示错误。
-
两个点之间的连线不能弯曲。
-
每个点只能“使用”一次，不可重复。这里的“使用”是指手指划过一个点，该点变绿。
-
两个点之间的连线不能“跨过”另一个点，除非那个点之前已经被“使用”过了。
对于最后一条规则，参见下图的解释。左边两幅图违反了该规则; 而右边两幅图(分别为2->4-1-3-6 和6->5-4->1->9-2) 则没有违反规则，因为在“跨过”点时，点已经被“使用”过了。
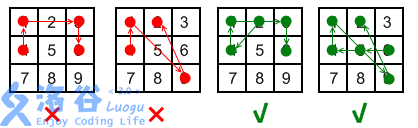
现在工程师希望改进解锁屏幕，增减点的数目，并移动点的位置，不再是一个九宫格形状，但保持上述画线的规则不变。请计算新的解锁屏幕上，一共有多少满足规则的画线方案。
输入输出格式
输入格式：
输入文件第一行，为一个整数n,表示点的数目。
接下来n 行，每行两个空格分开的整数 x_ixi 和 y_iyi ,表示每个点的坐标。
输出格式：
输出文件共一行，为题目所求方案数除以100000007 的余数。
输入输出样例
说明
样例#1解释: 设4 个点编号为1到4,方案有1->2->3->4，2->1->3->4，3->2->1->4，2->3->1->4，及其镜像4->3->2->1,3->4->2->1,2->3->4->1，3->2->4->1。
对于30%的数据， 1≤n≤101≤n≤10
对于100%的数据， -1000≤x_i,y_i≤1000,1≤n<20−1000≤xi,yi≤1000,1≤n<20 。各点坐标不相同
不是很难想的状压，f[S][i]表示已经走了集合S中的点，且目前在点i 的方案数，直接转移就行了。
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int ha=100000007;
const int maxn=1100005;
inline int add(int &x,int y){ x+=y; if(x>=ha) x-=ha;}
int ci[35],n,m,px[35],py[35],BC[maxn];
int S[35][35],f[maxn][23],ans;
inline void init(){
ci[0]=1;
for(int i=1;i<=20;i++) ci[i]=ci[i-1]<<1;
for(int i=1;i<ci[20];i++) BC[i]=BC[i^(i&-i)]+1;
}
inline void prework(){
for(int i=0;i<n;i++)
for(int j=0;j<n;j++){
S[i][j]=ci[i]|ci[j];
for(int k=0;k<n;k++){
if(px[k]>max(px[i],px[j])||px[k]<min(px[i],px[j])) continue;
if(py[k]>max(py[i],py[j])||py[k]<min(py[i],py[j])) continue;
if((px[i]-px[j])*(py[i]-py[k])==(px[i]-px[k])*(py[i]-py[j])) S[i][j]|=ci[k];
}
}
}
inline void dp(){
for(int i=0;i<n;i++) f[ci[i]][i]=1;
for(int i=1;i<=n;i++)
for(int j=0;j<ci[n];j++) if(BC[j]==i)
for(int k=0;k<n;k++) if(f[j][k]){
if(i>=4) add(ans,f[j][k]);
for(int l=0;l<n;l++) if(!(ci[l]&j)&&BC[(j&S[k][l])^S[k][l]]==1) add(f[j|ci[l]][l],f[j][k]);
}
}
int main(){
init(),scanf("%d",&n);
for(int i=0;i<n;i++) scanf("%d%d",px+i,py+i);
prework(),dp();
printf("%d\n",ans);
return 0;
}
