LightOj 1336 Sigma Function

Discription

Sigma function is an interesting function in Number Theory. It is denoted by the Greek letter Sigma (σ). This function actually denotes the sum of all divisors of a number. For example σ(24) = 1+2+3+4+6+8+12+24=60. Sigma of small numbers is easy to find but for large numbers it is very difficult to find in a straight forward way. But mathematicians have discovered a formula to find sigma. If the prime power decomposition of an integer is

 

Then we can write,

 

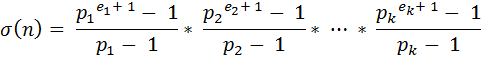
For some n the value of σ(n) is odd and for others it is even. Given a value n, you will have to find how many integers from 1 to n have even value of σ.

Input

Input starts with an integer T (≤ 100), denoting the number of test cases.

Each case starts with a line containing an integer n (1 ≤ n ≤ 10¹²).

Output

For each case, print the case number and the result.

Sample Input

4

3

10

100

1000

Sample Output

Case 1: 1

Case 2: 5

Case 3: 83

Case 4: 947

 

    首先发现2这个质因子没有用，所以我们就枚举每个数的2的次数是多少，然后/2^这个次数之后钦定它是奇数。

我们发现满足条件的数必须质因子里有至少一个的次数是奇数，所以直接补集转化减一下就行了。

 

#include<bits/stdc++.h>
#define ll long long
using namespace std;
int T;
ll ans,N;
inline ll g(ll x){ return (x+1)>>1;}
inline ll f(ll x){ return g(x)-g((ll)floor(sqrt(x+0.5)));}
int main(){
	scanf("%d",&T);
	for(int i=1;i<=T;i++){
		ans=0,scanf("%lld",&N);
		while(N) ans+=f(N),N>>=1;
		printf("Case %d: %lld\n",i,ans);
	}
	return 0;
}