[八省联考2018] 劈配
题目背景
一年一度的综艺节目《中国新代码》又开始了。Zayid 从小就梦想成为一名程序员,他觉得这是一个展示自己的舞台,于是他毫不犹豫地报名了。
题目描述
轻车熟路的Zayid 顺利地通过了海选,接下来的环节是导师盲选,这一阶段的规则是这样的:
总共n 名参赛选手(编号从1 至n)每人写出一份代码并介绍自己的梦想。接着 由所有导师对这些选手进行排名。为了避免后续的麻烦,规定不存在排名并列的情况。
同时,每名选手都将独立地填写一份志愿表,来对总共 m 位导师(编号从 1 至 m)作出评价。志愿表上包含了共m 档志愿。对于每一档志愿,选手被允许填写最多C 位导师,每位导师最多被每位选手填写一次(放弃某些导师也是被允许的)。
在双方的工作都完成后,进行录取工作。每位导师都有自己战队的人数上限,这意味着可能有部分选手的较高志愿、甚至是全部志愿无法得到满足。节目组对”前i 名的录取结果最优“ 作出如下定义:
-
前1 名的录取结果最优,当且仅当第1 名被其最高非空志愿录取(特别地,如 果第1 名没有填写志愿表,那么该选手出局)。
-
前i 名的录取结果最优,当且仅当在前i - 1 名的录取结果最优的情况下:第i 名 被其理论可能的最高志愿录取(特别地,如果第i 名没有填写志愿表、或其所有 志愿中的导师战队均已满员,那么该选手出局)。
如果一种方案满足‘‘前n 名的录取结果最优’’,那么我们可以简称这种方案是最 优的。
举例而言,2 位导师T 老师、F 老师的战队人数上限分别都是1 人;2 位选手 Zayid、DuckD 分列第1、2 名。那么下面3 种志愿表及其对应的最优录取结果如表中所示:
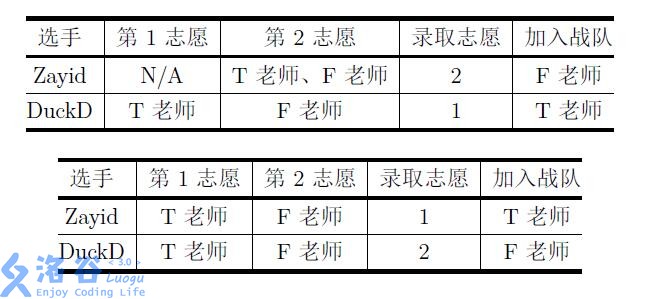
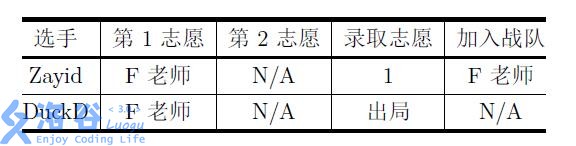
可以证明,对于上面的志愿表,对应的方案都是唯一的最优录取结果。
每个人都有一个自己的理想值si,表示第i 位同学希望自己被第si 或更高的志愿录取,如果没有,那么他就会非常沮丧。
现在,所有选手的志愿表和排名都已公示。巧合的是,每位选手的排名都恰好与它们的编号相同。
对于每一位选手,Zayid 都想知道下面两个问题的答案:
-
在最优的录取方案中,他会被第几志愿录取。
-
在其他选手相对排名不变的情况下,至少上升多少名才能使得他不沮丧。
作为《中国新代码》的实力派代码手,Zayid 当然轻松地解决了这个问题。不过他还是想请你再算一遍,来检验自己计算的正确性。
输入输出格式
输入格式:
从文件mentor.in 中读入数据。
每个测试点包含多组测试数据,第一行 2 个用空格隔开的非负整数 T;C,分别表示数据组数、每档志愿最多允许填写的导师数目。
接下来依次描述每组数据,对于每组数据:
-
第1 行两个用空格隔开的正整数n;m。
n;m 分别表示选手的数量、导师的数量。
-
第2 行m 个用空格隔开的正整数:其中第i 个整数为b_ibi 。
b_ibi 表示编号为i 的导师战队人数的上限。
-
第3 行至第n + 2 行,每行m 个用空格隔开的非负整数:其中第i + 2 行左起第 j 个数为a_{i,j}ai,j 。
a_{i,j}ai,j 表示编号为i 的选手将编号为j 的导师编排在了第a_{i,j}ai,j 志愿。特别地,如果a_{i,j}ai,j = 0,则表示该选手没有将该导师填入志愿表。
在这一部分,保证每行中不存在某一个正数出现超过 C 次(0 可能出现超 过C 次),同时保证所有a_{i,j}ai,j <= m。
-
第n + 3 行n 个用空格隔开的正整数,其中第i 个整数为s_isi 。
s_isi 表示编号为i 的选手的理想值。
在这一部分,保证s_isi <= m。
输出格式:
输出到文件mentor.out 中。
按顺序输出每组数据的答案。对于每组数据,输出2 行:
-
第1 行输出n 个用空格隔开的正整数,其中第i 个整数的意义为:
在最优的录取方案中,编号为i 的选手会被该档志愿录取。
特别地,如果该选手出局,则这个数为m + 1。
-
第 2 行输出 n 个用空格隔开的非负整数,其中第 i 个整数的意义为:
使编号为i 的选手不沮丧,最少需要让他上升的排名数。
特别地,如果该选手一定会沮丧,则这个数为i。
输入输出样例
说明
【样例1 解释】
三组数据分别与【题目描述】中的三个表格对应。
对于第1 组数据:由于选手1 没有填写第一志愿,所以他一定无法被第一志愿录 取,也就一定会沮丧。选手2 按原排名就不沮丧,因此他不需要提升排名。
对于第2 组和第3 组数据:1 号选手都不需要提升排名。而希望被第一志愿录取 的2 号选手都必须升到第1 名才能如愿。
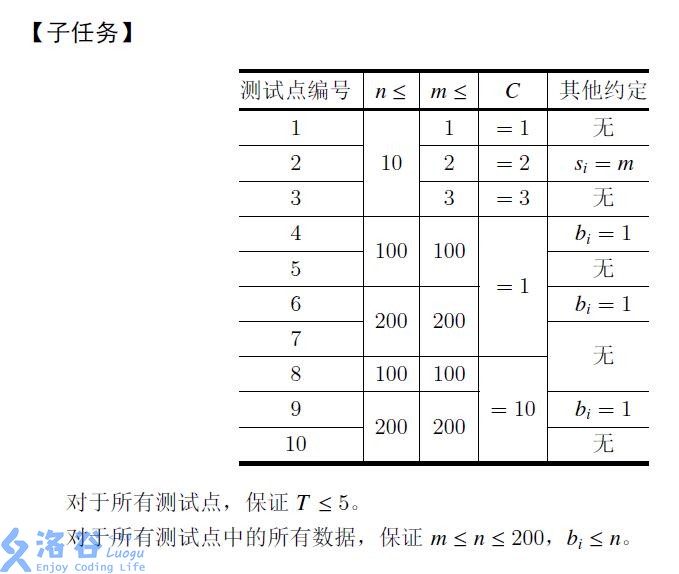
【样例2 解释】
1 号选手的第一志愿只填写了2 号导师,因此1 号选手必定被2 号导师录取。
2 号选手的第一志愿只填写了3 号导师,因此2 号选手必定被3 号导师录取。
由于2; 3 号导师均满员,且3; 4 号选手均填写了1 号导师,因此它们都会被1 号 导师录取。
所以1; 2 号选手均被第1 志愿录取,3 号选手被第3 志愿录取,4 号选手被第2 志 愿录取。
由于他们都如愿以偿了,所以他们都不需要提升名次。
有一个悲伤的故事是这样的,考场上看了这个题我本来是想往网络流上想的,但是怕T1耽误太久T2,T3没时间打暴力,所以我果断选择打了一个70分暴力。。。
结果呢? 学员出局的时候我TM忘了接着往下找了,,,T1最后直接爆零了23333,真是惨
昨天考完了心情一直很差,,,也没有听讲。。。
今天回过头来想一想,这个题真TM不就是个傻逼网络流吗23333,为什么当时考场上就这么怂,唉。。。。
回答第一问的时候,我们从前向后确定每个学员最优可以填第几个志愿。。。这个很好确定,当把一个志愿的边都加上之后如果有曾广路的话就是可行的。
然后第一问就这么做完了。
第二问其实也不难想。
首先如果一个学生i在第一问里的志愿就是<=s[i] 的话,直接返回0就行了;
然后我们先把这个学生的前s[i]志愿的边都连上,如果这个时候没有增广路那么返回i就行了,无解;
之后对于1到i-1的每一个j(按从小到大的顺序),连上所有最优志愿的边,然后分别看能不能增广,能的话就接着找,否则就说明i要跳到这个位置才能高兴。
然后就做完了,,再心疼day2的我60s 23333
#include<bits/stdc++.h>
#define ll long long
#define pb push_back
const int maxn=205;
using namespace std;
vector<int> g[maxn*3];
struct lines{
int to,flow,cap;
}l[maxn*maxn*3];
int S=0,T=401,t=-1;
int d[maxn*3],cur[maxn*3];
bool v[maxn*3];
inline void add(int from,int to,int cap){
l[++t]=(lines){to,0,cap},g[from].pb(t);
l[++t]=(lines){from,0,0},g[to].pb(t);
}
inline bool BFS(){
memset(v,0,sizeof(v));
queue<int> q;
int x; lines e;
q.push(S),v[S]=1,d[S]=0;
while(!q.empty()){
x=q.front(),q.pop();
for(int i=g[x].size()-1;i>=0;i--){
e=l[g[x][i]];
if(e.flow<e.cap&&!v[e.to]) v[e.to]=1,d[e.to]=d[x]+1,q.push(e.to);
}
}
return v[T];
}
int dfs(int x,int A){
if(x==T||!A) return A;
int flow=0,f,sz=g[x].size();
for(int &i=cur[x];i<sz;i++){
lines &e=l[g[x][i]];
if(d[x]==d[e.to]-1&&(f=dfs(e.to,min(A,e.cap-e.flow)))){
A-=f,flow+=f;
e.flow+=f,l[g[x][i]^1].flow-=f;
if(!A) break;
}
}
return flow;
}
inline int max_flow(){
int an=0;
while(BFS()){
memset(cur,0,sizeof(cur));
an+=dfs(S,1<<30);
}
return an;
}
vector<int> TC[maxn][maxn];
int Q,n,m,C,BEST[maxn],pre;
int b[maxn],s[maxn],now;
inline void init(){
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++) TC[i][j].clear();
for(int i=0;i<=T;i++) g[i].clear();
memset(BEST,0,sizeof(BEST));
}
inline void input(){
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++) scanf("%d",b+i);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++){
scanf("%d",&now);
if(now) TC[i][now].pb(j);
}
for(int i=1;i<=n;i++) scanf("%d",s+i);
}
inline int check(int x){
if(BEST[x]<=s[x]) return 0;
t=-1;
for(int i=0;i<=T;i++) g[i].clear();
add(S,x,1);
for(int i=1;i<=m;i++) add(i+n,T,b[i]);
for(int i=1;i<=s[x];i++)
for(int j=TC[x][i].size()-1;j>=0;j--) add(x,TC[x][i][j]+n,1);
if(!max_flow()) return x;
for(int i=1;i<x;i++){
if(BEST[i]>m) continue;
add(S,i,1);
for(int j=TC[i][BEST[i]].size()-1;j>=0;j--) add(i,TC[i][BEST[i]][j]+n,1);
if(!max_flow()) return x-i;
}
}
inline void solve(){
for(int i=1;i<=m;i++) add(n+i,T,b[i]);
for(int i=1;i<=n;i++){
add(S,i,1);
for(int j=1;j<=m;j++){
pre=t;
for(int k=TC[i][j].size()-1;k>=0;k--) add(i,TC[i][j][k]+n,1);
if(max_flow()){
BEST[i]=j;
break;
}
while(t>pre) g[l[t].to].erase(g[l[t].to].end()-1),t--;
}
if(!BEST[i]) BEST[i]=m+1;
}
for(int i=1;i<=n;i++) printf("%d ",BEST[i]);
puts("");
for(int i=1;i<=n;i++) printf("%d ",check(i));
puts("");
}
int main(){
scanf("%d%d",&Q,&C);
while(Q--){
init();
input();
solve();
}
return 0;
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号