[SDOI2010]代码拍卖会
题目描述
随着iPig在P++语言上的造诣日益提升，他形成了自己一套完整的代码库。猪王国想参加POI的童鞋们都争先恐后问iPig索要代码库。iPig不想把代码库给所有想要的小猪，只想给其中的一部分既关系好又肯出钱的小猪，于是他决定举行了一个超大型拍卖会。
在拍卖会上，所有的N头小猪将会按照和iPig的好感度从低到高，从左到右地在iPig面前站成一排。每个小猪身上都有9猪币（与人民币汇率不明），从最左边开始，每个小猪依次举起一块牌子，上面写上想付出的买代码库的猪币数量（1到9之间的一个整数）。大家都知道，如果自己付的钱比左边的猪少，肯定得不到梦寐以求的代码库，因此从第二只起，每只猪出的钱都大于等于左边猪出的价钱。最终出的钱最多的小猪（们）会得到iPig的代码库真传，向着保送PKU（Pig Kingdom University）的梦想前进。
iPig对自己想到的这个点子感到十分满意，在去现场的路上，iPig就在想象拍卖会上会出现的场景，例如一共会出现多少种出价情况之类的问题，但这些问题都太简单了，iPig早已不敢兴趣了，他想要去研究更加困难的问题。iPig发现如果他从台上往下看，所有小猪举的牌子从左到右将会正好构成一个N位的整数，他现在想要挑战的问题是所有可能构成的整数中能正好被P整除的有多少个。由于答案过大，他只想要知道答案mod 999911659就行了。
输入输出格式
输入格式：
输入文件auction.in有且仅有一行：两个数N（1≤N≤10^18）、P(1≤P≤500)，用一个空格分开。
输出格式：
输入文件auction.out有且仅有一行：一个数，表示答案除以999911659的余数。
输入输出样例
说明
样例解释
方案可以是：12 15 18 24 27 33 36 39 45 48 57 66 69 78 99，共15种。
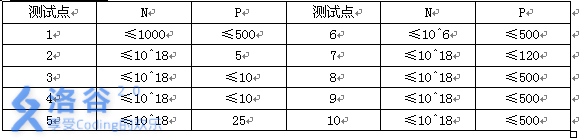
数据规模
这个题一不小心就往矩阵乘法上想了，，，，
但是矩乘肯定过不去啊。。。
恰好N位不太好处理，所以我们考虑一下<=N位的所有满足条件的数怎么求。
因为最大的位<=9，且后面的位都>=前面的位，所以我们考虑从 1,11,111,1111.....,1...1(n个1),中选不超过9个数(不能不选，且一个数可以选多次)，使得他们的和%P为0的方案数。
可以发现这样的方案数就是<=N位的数中满足条件的数的个数。
但现在有一个问题:那些数有n(<=10^18)个，太多了。
但是我们发现，选一个数对总和%P造成的影响只和 这个数%P的值有关，而P<=500，所以我们就可以把这些数分成不超过500个等价类，再记一下每个等价类中数的数量就行了。
直接找肯定是不行的，但我们发现11..1(i个1)=11..1(i-1个1)*10 + 1 (这不是废话嘛333)，也就是每个数在同余系下只有一条出边，这样我们就直接找环好了。
然后就是简单的dp过程了，懒得讲了(别忘了最后用N位的答案-N-1位的答案)。
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int ha=999911659;
ll N;
int P,num[505],now,ans,C[505][12];
int f[505][505][12],sum[505],inv[12];
bool v[505],flag=0;
inline int add(int x,int y,const int mod){
x+=y;
return x>=mod?x-mod:x;
}
inline void prework(){
int tag,len=0;
num[now=1]=1;
while(!v[num[now]]){
v[num[now]]=1;
num[now+1]=(num[now]*10+1)%P;
now++;
}
now--;
for(int i=1;i<=now;i++) if(num[i]==num[now+1]){
tag=i;
break;
}
for(int i=1;i<tag;i++) if(N>=i) sum[i]=1;
len=now-tag+1;
for(int i=tag;i<=now;i++) if(N>=i) sum[i]=((N-i)/len+1)%ha;
inv[1]=1;
for(int i=2;i<=10;i++) inv[i]=-inv[ha%i]*(ll)(ha/i)%ha+ha;
for(int i=1,T,S,tmp;i<=now;i++){
C[i][0]=1;
T=sum[i],S=tmp=1;
for(int j=1;j<=9;j++,T=add(T,1,ha)){
S=S*(ll)inv[j]%ha;
tmp=tmp*(ll)T%ha;
C[i][j]=tmp*(ll)S%ha;
}
}
}
inline void dp(){
f[0][0][0]=1;
for(int i=0;i<now;i++){
if(!sum[i+1]){
now=i;
break;
}
for(int j=0;j<P;j++)
for(int k=0,O,U;k<=9;k++) if(f[i][j][k]){
O=f[i][j][k],U=j;
for(int l=0;l+k<=9;l++,U=add(U,num[i+1],P)){
f[i+1][U][l+k]=add(f[i+1][U][l+k],O*(ll)C[i+1][l]%ha,ha);
}
}
}
}
inline void calc(){
for(int i=1;i<=9;i++)
if(!flag) ans=add(ans,f[now][0][i],ha);
else ans=add(ans,ha-f[now][0][i],ha);
}
inline void init(){
memset(v,0,sizeof(v));
memset(f,0,sizeof(f));
memset(sum,0,sizeof(sum));
}
int main(){
scanf("%lld%d",&N,&P);
prework();
dp();
calc();
init(),N--,flag=1;
prework();
dp();
calc();
printf("%d\n",ans);
return 0;
}
