某考试 T1 Function

1 Function

    function.cpp/in/out

    Time limit: 2s

    Memory limit: 512MB

 

1.1 Description

    给定 m 元不等式组

    ∀1 ≤ i ≤ n, xi ≤ t , 且∑ xi ≤ S 。

    给定 S, t, n, m，其中 n ≤ m，

    求不等式的正整数解的个数对 109 + 7 取模后的结果

 

1.2 Input Format

    第一行四个正整数 S, t, n, m

 

1.3 Output Format

    输出一行一个数字表示答案.

 

1.4 Sample Input

    7 2 3 4

 

 

1.5 Sample Output

    20

 

1.6 Constraints

    对于 10% 的数据满足 S, t, n, m ≤ 20

    对于另 20% 的数据满足 S, m ≤ 10^6

    对于另 30% 的数据满足 m − n ≤ 100

    对于 100% 的数据满足 nt ≤ S ≤ 10^18, n ≤ m ≤ 10^9 , t ≤ 10^9 , m − n ≤ 1000

 

    这里因为我不会正解，所以想看正解的童鞋可以去查一下2018年国家集训队作业的杭州二中某神犇的论文，，，反正我也不会。

    

    但为什么我还要写博客呢？ 因为我考试的时候yy出了一个 (m-n)^3 的做法，常数还蛮小的，在雅礼机房电脑(没开O2，且性能不是很好)跑了大概4秒多能出最大数据，于是就果断交了。。。。结果考试后发现被卡的只有40分(按理说老师电脑那么好再开O2我应该是能跑过的啊qwq)。

    晚上会宾馆开O2测了一下，具体情况如下图:

 

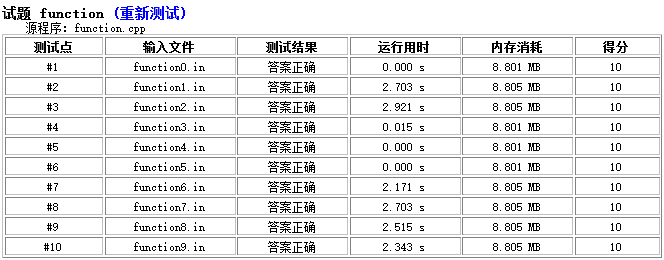
   所以我考场上把所有long long（除了记S的）都改成int 可能就能卡过了23333.

 

    讲了这么多废话现在来说一下我怎么做的吧。

    首先先假设 前n个变量的值已经确定了，那么剩下m-n个变量取值的所有可能种数就是 C(S-Σx[i](i<=n) , m-n) ，这个用隔板法推一推就行了，后面m-n个变量最少取1，和<=S-Σx[i](i<=n) 就相当于再加一个>=0的变量 = S-Σx[i](i<=n) 的方案数。

    因为始终是？个选m-n个的组合数，所以我们把这个组合数展开，提出一个 1/(m-n)! ,剩下的就是一个 S-Σx[i](i<=n) 的m-n次下降幂，然后我们就可以把 Σx[i](i<=n) 看成一个变量，把前面的 S-i （因为是下降幂嘛） 看成一个常数，来进行暴力多项式乘法 (是不是看起来很zz的操作2333)。这样的复杂度是 O((m-n)^2) 的。

   

    我们把多项式乘出来之后，答案就是一个形如 a[0] * (Σx[i](i<=n))^0 + a[1] * (Σx[i](i<=n))^1 +....  +a[m-n] * (Σx[i](i<=n))^(m-n) 的东西。

    你问我为什么a[0]后面乘了一个 (Σx[i](i<=n))^0 ？这个玩意不是不管括号里面是啥(注意前n个x的和一定为正整数)都始终为1吗？

但还真不是这样的，因为我这里的 (Σx[i](i<=n))^0 代表的意思是 所有可能的序列x[]的和的0次方的和，也就是有多少种可能的序列x[]。当指数不为0的时候意义类似，就是方案数再加权一下。

    

    然后就到了本题最难也是最精妙的部分了：如何求 (Σx[i](i<=n))^k 在所有可能序列x[]的情况下的和 (其实可以写成 Σ (Σx[i](i<=n))^k ，但是太丑了23333)。

设 f(n,k) 为 (Σx[i](i<=n))^k 在所有可能序列x[]的情况下的和，那么我们尝试把 x[2]+x[3]...+x[n] 看成一个整体，然后把 (Σx[i](i<=n))^k 二项式展开一下，可以得到 f(n,k) = n * Σ f(n-1,j) * sum{ t , k-j } * C(k-1,j)    ,其中j<k , k>0 , sum{ x , y } 表示 1^y+2^y+....x^y。然后 f(n,0) = t^n.

 

    先尚且不管 组合数 和sum{} 怎么预处理，而是来考虑一下这个式子的意义。

一般的人看了这个内心肯定会有如下几个疑问：1.为什么Σ前面要 * 一个n ？ 2.为什么没有 x[1]^0 的情况 3.为什么二项式系数不是 C(k,?) 而是C(k-1,?)。

    

    1.首先这n个变量的限制是一样的，所以如果我们把每个x[i]单独剥离出来之后，答案都是一样的，所以我们就只算把x[1]剥离出来的答案，然后再乘上n就是最后的答案。

    2.之所以要钦定x[1]的次数>0，是因为如果把上式完全展开之后的某一项如果没有x[1]，而我们把它算进来了，那么答案会变大，因为任意一个没有x[1]的项再将只考虑x[1]的答案*n之后都可以被一个含x[1]的项表示，也就是x[]之间可以互相等价转化。

    3.解释了上面一个之后，这个问题的答案就显然了，因为钦定x[1]的次数至少是1，也就是钦定第一个括号里的项变成x[1]，于是二项式系数

就变成了C(k-1,?)。

 

    然后终于解决了这个题最恶心的部分，，，现在来说一下怎么预处理 组合数 和 sum{}。

组合数很好说，里面的两项都是<=m-n的，所以我们直接 O((m-n)^2) 预处理都可以。

但是这个自然幂数和就比较恶心了，，，t是10^9级别的，并且次数 k 是10^3级别的，这个既无法暴力算又无法消元消出多项式，所以拉格朗日插值？？？

    的确是可以拉格朗日插值的，复杂度是 O((m-n)^2) 的  (或者用牛顿插值能更快？)，但是毕竟懒得写那么多，于是我用了一种更加简单的方法(可能这个部分就5行？)。 

    考虑把 (n+1)^(k+1) 展开，然后重复把指数是(k+1)的项展开，可以得到以下的式子:

         (n+1)^(k+1) = ΣC(k+1,1) * sum{ n , k } + Σ C(k+1,2) * sum{ n , k-1 } + ..... 

    因为本题的n是固定的(就是t)，于是我们就可以暴力的 在O((m-n)^2) 时间里递推出 所有的 sum{ n , 1~k}。

 

    最后回答一下可能存在的小疑问，就是之前的dp部分: f(n,k) 中的k最大是m-n，这个还好说，但是 n 可能到10^9 ，这可怎么dp啊？

 考虑到 f(n,0) 可以直接计算，并且 k>0 的 f(n,k) 只和 f(n-1,0~k-1) 有关，而我们最后要求的是所有的 f(n(这个是题目中给的)，1~m-n)，所以可以发现只有 f(i,0~m-n-(n-i)) 会被用到，其中n-(m-n) <= i <=n， 所以就可以开开心心写O((m-n)^3)的dp了 (状态 O((m-n)^2),转移O(m-n))。

 

    虽然我证明了常数只有1/6，但直接写的话还是会T的只有40分的23333，只有卡卡常数才能过，游戏体验极差。

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<algorithm>
#include<cmath>
#include<cstring>
#define ll long long
using namespace std;
const int ha=1000000007;
const int maxn=1005;
ll S,T,N,M,C[maxn][maxn],k,sum[maxn];
ll ans=0,X[maxn],a[maxn],tp,f[maxn];

inline ll add(ll x,ll y){
	x+=y;
	return x>=ha?x-ha:x;
}

inline ll ksm(ll x,ll y){
	ll an=1;
	for(;y;y>>=1,x=x*x%ha) if(y&1) an=an*x%ha;
	return an;
}

inline void init(){
	C[0][0]=1;
	for(int i=1;i<=1001;i++){
		C[i][0]=1;
		for(int j=1;j<=i;j++) C[i][j]=add(C[i-1][j-1],C[i-1][j]);
	}
}

inline void prework(){
	a[0]=1,tp=0,S%=ha;
	for(int i=0;i<k;i++,S=add(S,ha-1)){
		tp++;
		for(int j=tp;j;j--) a[j]=add(a[j]*S%ha,a[j-1]*(ll)(ha-1)%ha);
		a[0]=a[0]*S%ha;
	}
}

inline void work(ll n,ll u){
	for(int i=u;i;i--){
		f[i]=0;
		for(int j=0;j<i;j++) f[i]=add(f[i],f[j]*sum[i-j]%ha*C[i-1][j]%ha);
		f[i]=f[i]*n%ha;
	}
	f[0]=ksm(T,n);
}

inline void getX(){
	ll o=T;
	sum[0]=o+1;
	for(int i=1;i<=k;i++){
		sum[i]=ksm(o+1,i+1);
		for(int j=0;j<i;j++) sum[i]=add(sum[i],ha-sum[j]*C[i+1][j]%ha);
		sum[i]=sum[i]*ksm(i+1,ha-2)%ha;
	}
	
	for(ll i=max(0ll,N-k);i<=N;i++){
		work(i,i-(N-k));
	}
}

inline void calc(){
	for(int i=0;i<=k;i++) ans=add(ans,a[i]*f[i]%ha);
	ll inv=1;
	for(int i=1;i<=k;i++) inv=inv*(ll)i%ha;
	inv=ksm(inv,ha-2);
	ans=ans*inv%ha;
}

inline void solve(){
	prework();
	getX();
	calc();
}

int main(){
	freopen("function.in","r",stdin);
	freopen("function.out","w",stdout);
	
	init();
	cin>>S>>T>>N>>M;
	
	if(N==M){
		if(N*T<S) puts("0");
		else puts("1");
		return 0;
	}
	
	k=M-N,solve();
	cout<<ans<<endl;
	return 0;
}