某考试 T3 bitboard
bitboard
Discription
天才发明家小K 制造了一块比特板。板子上有2^n个比特元,编号为0 ∼ 2^n−
1。每个比特元𝑖可以接受一个[0,2^m)之间的整数作为输入信号,并产生整数𝑝(作
为固定的输出信号。当编号为𝑖的比特元接收到输入信号𝑗时,将生成𝑊(𝑖, 𝑗)枚比
特币。
相似的比特元之间还会产生叠加效果。每个比特元𝑖有一个饱和值𝑡(。如果两
个比特元的编号𝑎和𝑏在二进制下只有一位不同,并且两个比特元中的至少一个
接收到的输入信号不小于其饱和之时,这两个比特元将额外生成𝑝i xor 𝑝j 枚比特
币。请注意,饱和值的取值范围是[0,2^m]。
小K 希望给每个比特元适当的输入信号,使得比特版生成的比特币总数尽
量多。小K 觉得这个问题太简单了,于是他把问题交给你来解决。
Input
输入数据第一行包含两个整数𝑛和𝑚。
第二行包含2^n个整数𝑡i,代表每个比特元的饱和值。
第三行包含2^n个整数𝑝i,代表每个比特元的固定输出信号。
接下来2^n行,每行2^m个整数,代表𝑊(𝑖, 𝑗)。由于比特币是虚拟货币,所以
𝑊(𝑖, 𝑗)可能是负数。
Output
输出一行,包含一个整数,代表最多能生成的比特币数。
Sample Input
3 2
0 1 1 3 3 0 3 3
4 8 8 7 0 9 2 9
-9 -8 3 2
-9 -6 4 1
-6 -8 -5 3
3 -1 -4 -1
-6 -5 1 10
-10 7 3 -10
-3 -10 -4 -5
-2 -1 -9 1
Sample Output
133
Hint
对于20%的数据,𝑛 ≤ 3,𝑚 ≤ 2。
另外有20%的数据,𝑡= 0或2^m。
另外有20%的数据,𝑚 = 1。
对于100%的数据,1 ≤ 𝑛 ≤ 8,1 ≤ 𝑚 ≤ 8,0 ≤ 𝑡i ≤ 2^m,0 ≤ 𝑝i , |𝑊(𝑖, 𝑗)| ≤
2^10。
老师给的标解是O(2^(n+m)+2^(n*2)),跑的巨慢,而且还不是很好理解(什么负边+一个最大边都不可能到的值),根本无法意会他讲了什么233。
于是今天我就从最小割的方面想了想,调了调,最后可算是A了。我的复杂度是O(2^(n*2)),并且评测速度艹爆了标程23333。
首先我们可以发现,很多W都没有用。其实对于每一个比特板i,我们只需要保留不饱和的最大W和饱和的最大W。
当然,会有一些比特板永远饱和或者不饱和,那么把它们的另一个状态设为-inf就行了。
我们还知道i^j的lowbit等于它本身的时候,i和j是可以有共同效应的。
所以i和j的二进制1的个数肯定是不一样的,这提示我们可以建二分图。
设二进制中1的个数是偶数的是白点,反之是黑点。
那么我们从S连向每个白点一条边,代表饱和;从白点向T连边,代表不饱和;对于黑点,我们相反建图,S连的代表不饱和,T连的代表饱和。
然后我们设每条边的权值为不选这一状态要付出的代价,这时会遇到个问题:
一个状态对应的权值可正可负,这时候应该怎么连?
如果选一个状态的收益是正的,那么我们先把答案加上这个值,然后把代表这个状态的边的容量加上这个收益,代表如果割了这条边(不选这个状态)就要付出这么多代价;
如果一个状态的收益是负的,那么我们直接把代表这个状态的否状态(即饱和的否状态对应不饱和)的容量加上这个收益的绝对值,代表如果割了它的否状态(就是选了这个状态)就要付出这个代价。这种情况同样适用于这个状态不存在的情况,因为此时不存在的状态的否状态的边的容量就是inf,是肯定不能被割的,所以肯定得被选。
还有一个问题,那就是怎么表示额外生成的比特币?
当然可以先把答案加上这个额外比特币然后再在图中连边表示不额外生成的代价。
随便画一个草图观察一下,可以发现从黑点连向白点的有向边可以表示两个点都不饱和的时候必须割这条边。
至此,这个题已经被完美解决2333
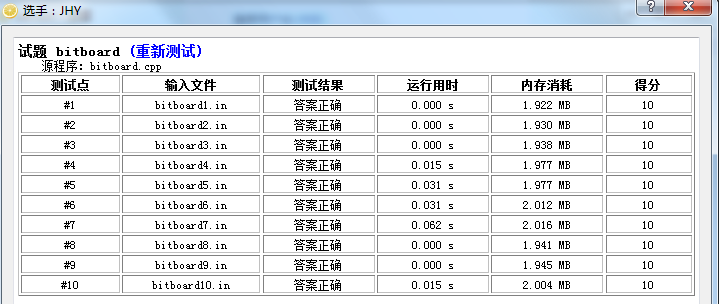
别看我说了这么多,其实代码更多23333
#include<bits/stdc++.h>
#define ll long long
#define pb push_back
#define maxn 2005
using namespace std;
vector<int> g[maxn];
struct lines{
int to,flow,cap;
}l[maxn*maxn];
int ci[30],n,m,p[maxn],E[maxn];
int S,T,t=-1,d[maxn],cur[maxn];
int val[maxn][2],tot=0,now;
int inside[maxn],outside[maxn];
bool v[maxn],col[maxn];
inline void add(int from,int to,int cap){
l[++t]=(lines){to,0,cap},g[from].pb(t);
l[++t]=(lines){from,0,0},g[to].pb(t);
}
inline bool BFS(){
memset(v,0,sizeof(v));
queue<int> q;
q.push(S),v[S]=1,d[S]=0;
int x; lines e;
while(!q.empty()){
x=q.front(),q.pop();
for(int i=g[x].size()-1;i>=0;i--){
e=l[g[x][i]];
if(e.flow<e.cap&&!v[e.to]){
v[e.to]=1,d[e.to]=d[x]+1;
q.push(e.to);
}
}
}
return v[T];
}
int dfs(int x,int a){
if(!a||x==T) return a;
int flow=0,f,sz=g[x].size();
for(int &i=cur[x];i<sz;i++){
lines &e=l[g[x][i]];
if(d[e.to]==d[x]+1&&(f=dfs(e.to,min(a,e.cap-e.flow)))){
a-=f,flow+=f;
e.flow+=f,l[g[x][i]^1].flow-=f;
if(!a) break;
}
}
return flow;
}
inline int max_flow(){
int an=0;
while(BFS()){
memset(cur,0,sizeof(cur));
an+=dfs(S,1<<30);
}
return an;
}
inline bool can(int x){
return (x&-x)==x;
}
inline void build(){
S=n,T=n+1;
col[0]=0;
for(int i=1;i<=ci[12];i++) col[i]=!col[i^(i&-i)];
for(int i=0;i<n;i++){
if(col[i]){
if(val[i][0]>0){
tot+=val[i][0];
inside[i]+=val[i][0];
}
else outside[i]-=val[i][0];
if(val[i][1]>0){
tot+=val[i][1];
outside[i]+=val[i][1];
}
else inside[i]-=val[i][1];
}
else{
if(val[i][0]>0){
tot+=val[i][0];
outside[i]+=val[i][0];
}
else inside[i]-=val[i][0];
if(val[i][1]>0){
tot+=val[i][1];
inside[i]+=val[i][1];
}
else outside[i]-=val[i][1];
}
}
for(int i=0;i<n;i++){
add(S,i,inside[i]);
add(i,T,outside[i]);
}
for(int i=0;i<n;i++) if(!col[i])
for(int j=0;j<n;j++) if(col[j]&&can(i^j))
tot+=p[i]^p[j],add(j,i,p[i]^p[j]);
}
/*
inline void check(){
for(int i=0;i<=n+1;i++){
if(i==n) puts("S: ");
else if(i>n) puts("T: ");
else printf("%d: ",i);
for(int j=g[i].size()-1;j>=0;j--){
lines e=l[g[i][j]];
if(e.flow==e.cap) printf("%d %d,",e.to,e.flow);
}
puts("");
}
}
*/
int main(){
freopen("bitboard.in","r",stdin);
freopen("bitboard.out","w",stdout);
ci[0]=1,memset(val,-0x3f,sizeof(val));
for(int i=1;i<=20;i++) ci[i]=ci[i-1]<<1;
scanf("%d%d",&n,&m),n=ci[n],m=ci[m];
for(int i=0;i<n;i++) scanf("%d",E+i);
for(int i=0;i<n;i++) scanf("%d",p+i);
for(int i=0;i<n;i++)
for(int j=0;j<m;j++){
scanf("%d",&now);
if(j>=E[i]) val[i][1]=max(val[i][1],now);
else val[i][0]=max(val[i][0],now);
}
build();
tot-=max_flow();
printf("%d\n",tot);
// check();
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号