某考试 T2 Tree

2 树

2.1 题目描述

给一棵n 个节点的树，节点分别编号为0 到n - 1。
你可以通过如下的操作来修改这棵树：首先先删去树上的一条边，此时树
会分裂为两个连通块，然后在两个连通块之间加上一条新的边使得它们变成一
棵新的树。
问有多少棵n 个节点的树可以通过对原树进行不超过k 次这样的操作来
得到，答案对109 + 7 取模。如果有一条边(u; v) 出现在了树A 中且不在树B
中，我们就认为树A 和树B 是不同的。
2.2 输入格式
第一行为两个整数n; k。
接下来一行用n - 1 个整数a1; a2; a3; :::; an-1 描述给定的树。其中ai 表
示节点i 和节点ai 之间有一条边，保证ai < i。
2.3 输出格式
输出一个整数表示答案对109 + 7 取模后的值。

2.4 输入样例一
3 1
0 0

2.5 输出样例一
3

 

2.6 输入样例二
6 4
0 1 1 3 3

2.7 输出样例二
1196

 

2.8 输入样例三
20 10
0 0 1 1 3 2 3 0 1 7 5 9 4 0 6 15 14 10 15

2.9 输出样例三
540101309

 

2.10 数据范围与约定
对于100% 的数据，n<=80，k<n。

 

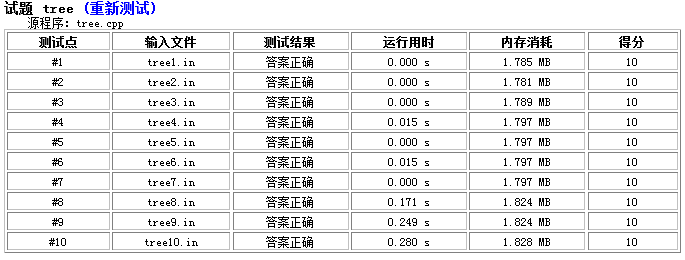
当时考试的时候先做的T1和T3然后就没时间做这个题了，，，

但是可能当时我有时间也做不出来吧23333.

 

正解是矩阵树定理+高斯消元/拉格朗日插值法。

因为最多只能选k条不是原来树上的边，所以我们可以把树边看成1，把非树边看成x。

最后的答案就是矩阵树定理消出的多项式的x^k及之前的项的系数和。

 

这个当然可以暴力多项式乘法(因为多项式的项数不多但是有很多多项式要相乘，所以此时的NTT是没有暴力快的)，

但是这样太慢了，大数据会挂。

 

我们还可以发现最后的多项式是一个n-1次多项式，所以我们可以带n对点来确定这个多项式。

这样的复杂度是 O(N^4) ，开开心心过本题。。。

 

 

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn=87;
const int ha=1000000007;
int n,k,a[maxn][maxn];
int fa,b[maxn][maxn];
int c[maxn][maxn],ans;

inline int add(int x,int y){
	x+=y;
	return x>=ha?x-ha:x;
}

inline int ksm(int x,int y){
	int an=1;
	for(;y;y>>=1,x=x*(ll)x%ha) if(y&1) an=an*(ll)x%ha;
	return an;
}

inline int matrix_tree(int x){
	int an=1;
	memset(b,0,sizeof(b));
	for(int i=1;i<=n;i++)
	    for(int j=i+1;j<=n;j++){
	    	if(a[i][j]) b[i][j]=b[j][i]=ha-1,b[i][i]++,b[j][j]++;
	    	else b[i][j]=b[j][i]=ha-x,b[i][i]+=x,b[j][j]+=x;
		}
	
	for(int i=1;i<n;i++){
		int tmp=i;
		for(;tmp<n;tmp++) if(b[tmp][i]) break;
		if(tmp>i){
			an=ha-an;
			for(int k=i;k<n;k++) swap(b[i][k],b[tmp][k]);
		}
		
		for(int j=i+1;j<n;j++)
		    while(b[j][i]){
		    	an=ha-an;
		    	int A=b[i][i]/b[j][i];
		    	for(int k=i;k<n;k++){
		    		b[i][k]=((ll)b[i][k]-b[j][k]*(ll)A)%ha;
		    		if(b[i][k]<0) b[i][k]+=ha;
		    		swap(b[i][k],b[j][k]);
				}
			}
		
		an=an*(ll)b[i][i]%ha;
	}
	
	return an;
}

inline void xy(){
	n++;
	for(int i=1;i<n;i++){
		if(!c[i][i]){
			for(int j=i+1;j<n;j++) if(c[j][i]){
				for(int k=i;k<=n;k++) swap(c[j][k],c[i][k]);
				break;
			}
		}
		
		for(int j=i+1;j<n;j++)
		    while(c[j][i]){
		    	int A=c[i][i]/c[j][i];
		    	for(int k=i;k<=n;k++){
		    		c[i][k]=((ll)c[i][k]-c[j][k]*(ll)A)%ha;
		    		if(c[i][k]<0) c[i][k]+=ha;
		    		swap(c[i][k],c[j][k]);
				}
			}
	}
	
	for(int i=n-1;i;i--){
		for(int j=n-1;j>i;j--) c[i][n]=add(c[i][n],add(ha,-c[j][n]*(ll)c[i][j]%ha));
		c[i][n]=c[i][n]*(ll)ksm(c[i][i],ha-2)%ha;
	}
}

int main(){
	freopen("tree.in","r",stdin);
	freopen("tree.out","w",stdout);
	
	scanf("%d%d",&n,&k);
	for(int i=2;i<=n;i++){
		scanf("%d",&fa);
		fa++,a[i][fa]++,a[fa][i]++;
	}
	
	for(int i=1;i<=n;i++){
		for(int j=1,u=1;j<=n;j++,u=u*(ll)i%ha) c[i][j]=u;
		c[i][n+1]=matrix_tree(i);
	}
	
	xy();
	
	k++;
	for(int i=1;i<=k;i++) ans=add(ans,c[i][n]);
	
	printf("%d\n",ans);
	
	return 0;
}