Codeforces 939 E Maximize!
题目描述
You are given a multiset S consisting of positive integers (initially empty). There are two kind of queries:
- Add a positive integer to S , the newly added integer is not less than any number in it.
- Find a subset s of the set S such that the value
![]() is maximum possible. Here max(s)max(s) means maximum value of elements in ss ,
is maximum possible. Here max(s)max(s) means maximum value of elements in ss , ![]() — the average value of numbers in s . Output this maximum possible value of
— the average value of numbers in s . Output this maximum possible value of ![]() .
.
输入输出格式
输入格式:
The first line contains a single integer Q ( 1<=Q<=5·10^{5}1<=Q<=5⋅105 ) — the number of queries.
Each of the next Q lines contains a description of query. For queries of type 1 two integers 1 and x are given, where x ( 1<=x<=10^{9}1<=x<=109 ) is a number that you should add to S . It's guaranteed that x is not less than any number in S . For queries of type 2 , a single integer 2 is given.
It's guaranteed that the first query has type 1 , i. e. S is not empty when a query of type 2 comes.
输出格式:
Output the answer for each query of the second type in the order these queries are given in input. Each number should be printed in separate line.
Your answer is considered correct, if each of your answers has absolute or relative error not greater than 10^{-6}10−6 .
Formally, let your answer be aa , and the jury's answer be bb . Your answer is considered correct if 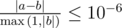 .
.
输入输出样例
2.0000000000
首先一定要选最大的元素。
为什么呢?
假设有一个最优方案没有最大的元素,那么我们把这个方案里的最大元素替换成当前最大值,
那么max*num-tot一定会增加(前一项增加(now_max-pre_max)*num,后一项增加now_max-pre_max,又因为num>=1)
答案又是(max*num-tot)/num,所以嘛、、、、
然后我是二分的斜率,反正是个离散函数,定义域只有正整数。
#include<iostream>
#include<cmath>
#include<algorithm>
#include<cstdlib>
#include<cstdio>
#include<cstring>
#include<vector>
#include<queue>
#define ll long long
#define maxn 500005
using namespace std;
int n,Q,opt,now;
int l,r,mid,an;
ll num[maxn];
double ans=0;
inline double f(int x){
return (num[x]+(ll)now)/(double)(x+1);
}
int main(){
scanf("%d",&Q);
while(Q--){
scanf("%d",&opt);
if(opt==1){
n++;
scanf("%lld",num+n);
now=num[n];
num[n]+=num[n-1];
}
else{
l=1,r=n-1,an=0;
while(l<=r){
mid=l+r>>1;
if(f(mid)-f(mid-1)<0) an=mid,l=mid+1;
else r=mid-1;
}
ans=now-f(an);
printf("%lf\n",ans);
}
}
return 0;
}



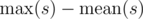 is maximum possible. Here
is maximum possible. Here 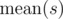 — the average value of numbers in
— the average value of numbers in 
 浙公网安备 33010602011771号
浙公网安备 33010602011771号