Codeforces 716 E Digit Tree
ZS the Coder has a large tree. It can be represented as an undirected connected graph of n vertices numbered from 0 to n - 1 and n - 1edges between them. There is a single nonzero digit written on each edge.
One day, ZS the Coder was bored and decided to investigate some properties of the tree. He chose a positive integer M, which is coprime to 10, i.e. 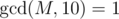 .
.
ZS consider an ordered pair of distinct vertices (u, v) interesting when if he would follow the shortest path from vertex u to vertex v and write down all the digits he encounters on his path in the same order, he will get a decimal representaion of an integer divisible by M.
Formally, ZS consider an ordered pair of distinct vertices (u, v) interesting if the following states true:
- Let a1 = u, a2, ..., ak = v be the sequence of vertices on the shortest path from u to v in the order of encountering them;
- Let di (1 ≤ i < k) be the digit written on the edge between vertices ai and ai + 1;
- The integer
![]() is divisible by M.
is divisible by M.
Help ZS the Coder find the number of interesting pairs!
The first line of the input contains two integers, n and M (2 ≤ n ≤ 100 000, 1 ≤ M ≤ 109, 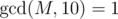 ) — the number of vertices and the number ZS has chosen respectively.
) — the number of vertices and the number ZS has chosen respectively.
The next n - 1 lines contain three integers each. i-th of them contains ui, vi and wi, denoting an edge between vertices ui and vi with digit wi written on it (0 ≤ ui, vi < n, 1 ≤ wi ≤ 9).
Print a single integer — the number of interesting (by ZS the Coder's consideration) pairs.
6 7
0 1 2
4 2 4
2 0 1
3 0 9
2 5 7
7
5 11
1 2 3
2 0 3
3 0 3
4 3 3
8
虽然不是很难想但是差点调死我hhhhh
首先这道题和常规点分治不太一样的地方是,普通的点分治一般是无向路径,我们往往不用考虑起点和终点而是直接考虑路径的两个端点就行了。
但是本题是有向路径,不同的方向意味着不同的数字。
而且本题还要一个坑爹的地方是知道终点好找起点,但是知道起点不好找终点。。。。。
当然有两种解决方法:
1.对于当前的重心选任意两条路径统计一遍,再把在同一颗子树内的减掉。
2.考虑到起点要么比终点先被扫到,要么晚被扫到,那么我们就正反两遍常规的calc,这样还不用去重。
我就是用的第二种方法。。。
然后千万别忘了起点或终点是重心的情况,,,,但这样不太可能,因为这样例都过不了hhhh
对于点分的每层我们用map记录一下起点的情况,然后用扫到的终点更新答案。
至于怎么更新答案,就是一个式子,推一下就好了也不难hhhh
当然如果你把向下和向上的路径写反了(就像一开始的我)是要调很久的hhhh,因为样例里并没有长度>=3的路径。
#include<iostream> #include<cstdio> #include<cstdlib> #include<cstring> #include<cmath> #include<map> #include<algorithm> #define ll long long #define maxn 100005 using namespace std; map<int,int> mmp; int ci[maxn],n,m,num=0,b[maxn]; int to[maxn*2],ne[maxn*2]; int hd[maxn],sz,minn,root; int d[maxn],tot,ni[maxn]; int siz[maxn],val[maxn*2]; ll ans; bool done[maxn]; inline void add(int uu,int vv,int ww){ to[++num]=vv,ne[num]=hd[uu],hd[uu]=num,val[num]=ww; } void froot(int x,int fa){ siz[x]=1; int bal=0; for(int i=hd[x];i;i=ne[i]) if(!done[to[i]]&&to[i]!=fa){ froot(to[i],x); siz[x]+=siz[to[i]]; bal=max(bal,siz[to[i]]); } bal=max(bal,sz-siz[x]); if(bal<minn) minn=bal,root=x; } int fsiz(int x,int fa){ int an=1; for(int i=hd[x];i;i=ne[i]) if(!done[to[i]]&&to[i]!=fa){ an+=fsiz(to[i],x); } return an; } void dfs(int x,int fa,int dep,int dx,int dy,int tmp){ int tox=(ll)(m-dy)*(ll)ni[dep]%m; if(mmp.count(tox)) ans+=(ll)mmp[tox]; if(tmp){ if(!dx) ans++; if(!dy) ans++; } d[++tot]=dx; for(int i=hd[x];i;i=ne[i]) if(!done[to[i]]&&to[i]!=fa){ dfs(to[i],x,dep+1,((ll)dx+(ll)val[i]*(ll)ci[dep])%m,((ll)dy*10ll+(ll)val[i])%m,tmp); } } inline void calc(int pos,int va,int tmp){ int pre=tot+1; dfs(pos,pos,1,va,va,tmp); for(;pre<=tot;pre++){ if(!mmp.count(d[pre])) mmp[d[pre]]=1; else mmp[d[pre]]++; } } inline void work(int x,int trsiz){ sz=trsiz,minn=1<<29; froot(x,x); done[root]=1; int len=0; for(int i=hd[root];i;i=ne[i]) if(!done[to[i]]){ b[++len]=i; calc(to[i],val[i],0); } mmp.clear(),tot=0; for(;len;len--){ calc(to[b[len]],val[b[len]],1); } mmp.clear(),tot=0; for(int i=hd[root];i;i=ne[i]) if(!done[to[i]]){ work(to[i],fsiz(to[i],to[i])); } } void gcd(int aa,int bb,ll &xx,ll &yy){ if(!bb){ xx=1,yy=0; return; } gcd(bb,aa%bb,yy,xx); yy-=xx*(ll)(aa/bb); } inline int get_ni(int x){ ll xx,yy; gcd(x,m,xx,yy); return (xx+m)%m; } int main(){ scanf("%d%d",&n,&m); ci[0]=ni[0]=1; for(int i=1;i<=n;i++) ci[i]=(ll)ci[i-1]*10ll%m,ni[i]=get_ni(ci[i]); //printf("%d %d %d\n",i,ci[i],ni[i]); int uu,vv,ww; for(int i=1;i<n;i++){ scanf("%d%d%d",&uu,&vv,&ww),uu++,vv++; ww%=m; add(uu,vv,ww),add(vv,uu,ww); } work(1,n); cout<<ans<<endl; return 0; }


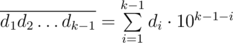 is divisible by
is divisible by 
 浙公网安备 33010602011771号
浙公网安备 33010602011771号