[TJOI2013]循环格

　　

题目背景

一个循环格就是一个矩阵,其中所有元素为箭头,指向相邻四个格子。每个元素有一个坐标(行,列),其中左上角元素坐标为(0,0)。给定一个起始位(r,c),你可以沿着箭头方向在格子间行走。即:如果(r,c)是一个左箭头，那么走到(r,c-1);如果是一个右箭头,走到(r,c+1);如果是上箭头,走到(r-1,c);如果是下箭头,走到(r+1,c)。每一行和每一列都是循环的,即如果走出边界,你会出现在另一侧。比如在一个5*5的循环格里,从(3,0)向左走会出现在(3,4)。

题目描述

一个完美的循环格是这样定义的:对于任意一个起始位置,你都可以沿着箭头最终回到起始位置。如果一个循环格不满足完美,你可以随意修改任意一个元素的箭头直到完美。例如下图,左边不是一个完美的循环格,因为只有从(1,1),(1,2),(2,0),(2,3)出发才会回到起始位置。通过修改其中两个箭头,可以得到右图,一个完美的循环格。

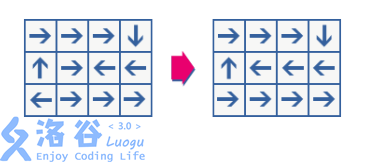
给定一个循环格,你需要计算最少需要修改多少个元素使其完美。

输入输出格式

输入格式：

 

第一行两个整数R和C,表示循环格的行和列。接下来R行,每一行包含C个字符LRUD表示左右上下

 

输出格式：

 

一个整数,表示最少需要修改多少个元素使得给定的循环格完美。

 

输入输出样例

输入样例#1：

4 4
RRRD
URDD
UULD
ULLL

输出样例#1：

0

输入样例#2： 

3 4
RRRD
URLL
LRRR

输出样例#2：

2

说明

数据范围

30%的数据，1 ≤ R, C ≤ 7

100%的数据，1 ≤ R, C ≤ 15

 

如果把网格中的点看成图中的点，可以发现每个点的出度都是1。

而满足条件的图肯定是若干个简单环，所以这就要求每个点的入度也是1。

然后就可以二分图匹配了，不过因为如果按照原来的方向走的话是不需要改变的，

所以还需要引入费用，跑一个最小费用最大流就行了。

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<algorithm>
#include<vector>
#include<queue>
#include<cstring>
#define ll long long
#define maxn 10005
#define pb push_back
using namespace std;
const int inf=1<<29;
vector<int> g[maxn]; 
struct lines{
    int from,to,flow,cap,cost;
}l[maxn*20];
int t=-1,S,T,n,m;
int d[maxn],p[maxn];
int a[maxn],ans=0;
bool iq[maxn];

inline void add(int from,int to,int cap,int cost){
    l[++t]=(lines){from,to,0,cap,cost},g[from].pb(t);
    l[++t]=(lines){to,from,0,0,-cost},g[to].pb(t);
}

inline bool BFS(){
    queue<int> q;
    memset(d,0x3f,sizeof(d));
    p[S]=0,a[S]=inf,iq[S]=1;
    d[S]=0,q.push(S);
    
    int x; lines e;
    while(!q.empty()){
        x=q.front(),q.pop();
        
        for(int i=g[x].size()-1;i>=0;i--){
            e=l[g[x][i]];
            if(e.flow<e.cap&&d[x]+e.cost<d[e.to]){
                d[e.to]=d[x]+e.cost;
                p[e.to]=g[x][i];
                a[e.to]=min(a[x],e.cap-e.flow);
                if(!iq[e.to]) iq[e.to]=1,q.push(e.to); 
            }
        }
        
        iq[x]=0;
    }
    
    if(d[T]==d[T+1]) return 0;
    
    ans+=a[T]*d[T];
    
    int now=T,pre;
    while(now!=S){
        pre=p[now];
        l[pre].flow+=a[T];
        l[pre^1].flow-=a[T];
        now=l[pre].from;
    }
    
    return 1;
}

inline void MFMC(){
    while(BFS());
}

//上1下2左3右4 
int id[25][25],num;
int val[maxn][6],dy[666];
char ch;

int main(){
    dy['L']=3,dy['R']=4;
    dy['U']=1,dy['D']=2;
    
    scanf("%d%d",&n,&m),S=0,T=2*n*m+1;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++){
            id[i][j]=++num;
            ch=getchar();
            while(!dy[ch]) ch=getchar();
            val[num][dy[ch]]=1;
        }
    
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++){
            int now=id[i][j];
            if(i==1) add(now,id[n][j]+num,1,val[now][1]^1);
            else add(now,id[i-1][j]+num,1,val[now][1]^1);
            
            if(i==n) add(now,id[1][j]+num,1,val[now][2]^1);
            else add(now,id[i+1][j]+num,1,val[now][2]^1);
            
            if(j==1) add(now,id[i][m]+num,1,val[now][3]^1);
            else add(now,id[i][j-1]+num,1,val[now][3]^1);
            
            if(j==m) add(now,id[i][1]+num,1,val[now][4]^1);
            else add(now,id[i][j+1]+num,1,val[now][4]^1);
        }
    
    
    for(int i=1;i<=num;i++){
        add(S,i,1,0);
        add(i+num,T,1,0);
    }
    
    MFMC();
    printf("%d\n",ans);
    return 0;
}