北京DAY1下午
省选模拟题
周子凯
题目概况
|
中文题目名 |
简易比特币 |
计算 |
路径 |
|
英文题目名 |
bit |
calculation |
Path |
|
输入文件名 |
bit.in |
calculation.in |
path.in |
|
输出文件名 |
bit.out |
calculation.out |
path.out |
|
每个测试点时限 |
1s |
2s |
1s |
|
内存限制 |
128M |
128M |
128M |
|
测试点数目 |
10 |
10 |
10 |
|
每个测试点分值 |
10 |
10 |
10 |
|
结果比较方式 |
全文比较(过滤行末空格及文末回车) |
||
|
题目类型 |
传统 |
||
1. 简易比特币
题目描述
相信大家都听说过比特币。它是一种虚拟货币,但与普通虚拟货币不同的是,它不由某个机构统一发行,而需要利用计算机找出具有特定性质的数据来“发现”货币,俗称“挖矿”。然而,由于具有这种特定性质的数据分布稀疏而无规律,因此挖矿的过程需要投入大量的计算资源来搜寻这些数据。
仿照比特币是设计思想,我们可以设计一种简易的比特币:给定一个由n个非负整数构成的序列{ai},和一个阈值K,如果某个非空子序列(一个连续的区间)中的所有数的异或和小于K,则这个子序列就对应了一个比特币,否则它毫无价值。
现在,给出这个序列和阈值,请你计算从中能获得多少个比特币。
严谨起见,简要解释一下什么是异或:
异或是一种位运算,Pascal中写作xor,C/C++中写作^。将两个数写成二进制形式,然后对每位作“相同得0、不同得1”的运算。例如,12 xor 6 = 10的运算方法如下:
12 = (1100)2
6 = (0110)2
ans= (1010)2 = 10
输入格式
第一行包含两个整数n和K,意义如题所述;
第二行包含n个非负整数ai,表示序列中的每一个数。
输出格式
一行包含一个整数,表示能从序列中获得的比特币数。
样例输入
3 2
1 3 2
样例输出
3
样例解释
1 = 1
1 xor 3 = 2
1 xor 3 xor 2 = 0
3 = 3
3 xor 2 = 1
2 = 2
一共3个区间的异或和小于2。
数据范围
对于20%的数据,n≤100;
对于40%的数据,n≤1000;
另有20%的数据,ai≤50;
对于100%的数据,1≤n≤105,0≤K≤109,0≤ai≤109。
2.计算
问题描述
我曾经的竞赛教练有一句名言:“人紧张起来的时候会变得和白痴一样的。”他总爱在比赛前重复这句话。其实论算法,他并没有教给我们多少,但是回想起以前的经历发现,至少这句话他说的真是太tm对了。用现在的话讲就是:不要怂,就是干。
oi题很多时候都是这样,乍一看很难,越看越觉得不可做,于是安慰自己说,肯定又是我没学过的某算法,做不出很正常。但抱有这种心理的,出了考场往往会被身边的神犇打脸:“这题其实先oo一下再xx一下就好了,我太弱了搞了一小时才搞出来……”
现在就有一道看上去似乎很不好搞的计算题,请你不怂地算一下怎么搞。
给出一个长为N的正整数序列,有三种操作:
A l r k b:在区间[l,r]上加上一个首项为b、公差为k的等差数列。即,序列al, al+1, al+2, al+3……变成al+b, al+1+b+k, al+2+b+2k, al+3+b+3k……
B l r:求区间[l,r]内所有数的和mod 1000000007的值
C l r:求区间[l,r]内所有数的平方的和mod 1000000007的值
输入格式
第一行包含两个数n、q,表示序列长度和操作的数量;
第二行包含n个数{ai},表示原序列;
接下来q行,每行包含一个操作,格式和意义如题面所述。
输出格式
输出若干行,每个B操作和C操作输出一行,表示询问的答案。
样例输入
3 3
1 1 1
A 1 3 2 2
B 1 2
C 2 3
样例输出
8
74
数据规模
测试点1~2:n, q ≤ 1000;
测试点3~4:k=0,没有C操作;
测试点5~6:k=0;
测试点7~8:没有C操作;
对于100%的数据,n, q ≤ 100000,0 ≤ ai, k, b ≤ 109,1 ≤ l ≤ r ≤ n
3. 路径
问题描述
实在不知道怎么编题面了,就写得直白一点吧。反正没几个人写得完三题,估计都看不到这里。
给出一个仙人掌图,求图中最长路的长度。
Emmm……还是稍微具体一点吧。
仙人掌图是指一个有N个点与M条边的无向图,点从1到N标号,每条边有各自的长度,图中可能存在若干个简单环,但是,每个点最多只会属于1个简单环路。简单环是指一个经过至少两个点、且不经过重复点的环。(这里仙人掌图的定义也许和你在别处见过的不太一样,请仔细审题)
例如,图1所示的是一个仙人掌图,但图2则不是,因为3号点同属于两个简单环。
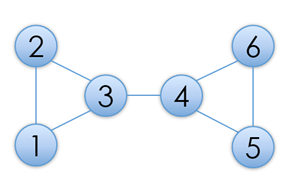
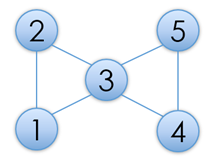
给出一个仙人掌图,你需要求出图中的最长路的长度。最长路不能经过重复的点。例如,假设图中所有边长度都为1的话,图1中的仙人掌图的一条最长路为1-2-3-4-5-6,长度为5。
输入格式
第一行包含1个整数Q,表示数据组数;
每组数据的第一行2个整数N,M,表示仙人掌图的点数和边数;
每组数据的接下来M行,每行3个正整数x,y,z,描述一条连接点x与点y,长度为z的边。
输出格式
对于每组数据输出一行,每行包含一个整数,表示最长路径的长度。
样例输入
2
6 7
1 2 1
2 3 1
3 1 1
3 4 1
4 5 1
5 6 1
6 4 1
4 4
1 2 1
2 3 2
3 4 3
4 1 4
样例输出
5
9
数据规模
对于10%的数据,Q ≤ 5,n ≤ 10;
另有20%的数据,满足n=m+1;
另有20%的数据,满足n=m;
另有20%的数据,满足每个环上的点数≤ 20;
对于100%的数据,Q ≤ 1000, 所有测试点的n之和 ≤ 100,000,z≤ 1000。
(T3图片可能被河蟹,没有就算了hhh)
今天T1就是Trie树上异或乱搞,T2玄学线段树标记应用(区间加等差数列,区间查询元素和和元素平方和)。
T3还没讲,,,(我明明写的50分暴力分啊,,,怎么多骗了20分hhh)
先粘一下我的代码
T1:
#include<iostream> #include<cstdio> #include<cstdlib> #include<cstring> #include<cmath> #include<algorithm> #define ll long long #define maxn 100005 using namespace std; int n,k,ch[maxn*35][2],siz[maxn*35]; int tot=0,val,now,ci[35],root=0; ll ans=0; inline int read(){ int x=0;char c=getchar(); for(;!isdigit(c);c=getchar()); for(;isdigit(c);c=getchar()) x=x*10+c-'0'; return x; } inline void ins(){ int pos=root,r; siz[0]++; for(int i=30;i>=0;i--){ r=(ci[i]&now)?1:0; if(!ch[pos][r]) ch[pos][r]=++tot; pos=ch[pos][r],siz[pos]++; } } inline int query(){ int pos=root,an=0,r; for(int i=30;i>=0;i--) if(k&ci[i]){ r=(now&ci[i])?1:0; if(ch[pos][r]) an+=siz[ch[pos][r]]; pos=ch[pos][r^1]; if(!pos) break; }else{ pos=ch[pos][(now&ci[i])?1:0]; if(!pos) break; } return an; } int main(){ freopen("bit.in","r",stdin); freopen("bit.out","w",stdout); ci[0]=1; for(int i=1;i<=30;i++) ci[i]=ci[i-1]<<1; n=read(),k=read(); now=0,ins(); for(int i=1;i<=n;i++){ val=read(); now^=val; ans+=(ll)query(); ins(); } cout<<ans<<endl; return 0; }
T2:
#include<iostream> #include<cstdio> #include<cstdlib> #include<cstring> #include<cmath> #include<algorithm> #define ll long long #define maxn 400005 #define ha 1000000007 using namespace std; ll hd[maxn],tag[maxn]; ll sum[maxn],sum_t[maxn]; ll sum_c[maxn],n,m,a[maxn>>1]; int le,ri,opt; ll k,b,pos,ans; char ch; bool ww; inline void pushup(int o,int lc,int rc,ll len){ sum[o]=sum[lc]+sum[rc]; if(sum[o]>=ha) sum[o]-=ha; sum_t[o]=sum_t[lc]+sum_t[rc]; if(sum_t[o]>=ha) sum_t[o]-=ha; sum_c[o]=(sum_c[lc]+sum_c[rc]+sum[rc]*len)%ha; } void build(int o,int l,int r){ if(l==r){ sum[o]=a[l],sum_t[o]=a[l]*a[l]%ha; return; } int mid=(l+r)>>1,lc=o<<1,rc=(o<<1)|1; build(lc,l,mid),build(rc,mid+1,r); pushup(o,lc,rc,mid+1-l); } inline ll ci1(ll x){ if(!x) return 0; return x*(x+1)/2%ha; } inline ll ci2(ll x){ if(!x) return 0; ll an=x*(x+1)>>1ll; if(!(an%3)) return an/3%ha*(x*2+1)%ha; else return (2*x+1)/3*(an%ha)%ha; } inline void change(int o,ll len,ll sx,ll gc){ hd[o]=(hd[o]+sx)%ha,tag[o]=(tag[o]+gc)%ha; sum_t[o]=(sum_t[o]+len*sx%ha*sx%ha+gc*gc%ha*ci2(len-1)%ha+2ll*sx%ha*sum[o]%ha)%ha; sum_t[o]=(sum_t[o]+2ll*sx%ha*gc%ha*ci1(len-1)%ha+2ll*gc%ha*sum_c[o]%ha)%ha; sum[o]=(sum[o]+sx*len%ha+ci1(len-1)*gc)%ha; sum_c[o]=(sum_c[o]+ci1(len-1)*sx%ha+gc*ci2(len-1))%ha; } inline void pushdown(int o,int l,int r){ if(hd[o]||tag[o]){ int mid=(l+r)>>1,lc=o<<1,rc=(o<<1)|1; change(lc,mid-l+1,hd[o],tag[o]); change(rc,r-mid,(hd[o]+tag[o]*(mid+1-l))%ha,tag[o]); hd[o]=tag[o]=0; } } void update(int o,int l,int r){ if(l>=le&&r<=ri){ change(o,r-l+1,(b+(ll)(l-le)*k)%ha,k); return; } pushdown(o,l,r); int mid=(l+r)>>1,lc=o<<1,rc=(o<<1)|1; if(le<=mid) update(lc,l,mid); if(ri>mid) update(rc,mid+1,r); pushup(o,lc,rc,mid+1-l); } ll query1(int o,int l,int r){ if(l>=le&&r<=ri) return sum[o]; pushdown(o,l,r); ll an=0,mid=(l+r)>>1,lc=o<<1,rc=(o<<1)|1; if(le<=mid) an+=query1(lc,l,mid); if(ri>mid) an+=query1(rc,mid+1,r); if(an>=ha) an-=ha; return an; } ll query2(int o,int l,int r){ if(l>=le&&r<=ri) return sum_t[o]; pushdown(o,l,r); ll an=0,mid=(l+r)>>1,lc=o<<1,rc=(o<<1)|1; if(le<=mid) an+=query2(lc,l,mid); if(ri>mid) an+=query2(rc,mid+1,r); if(an>=ha) an-=ha; return an; } int main(){ freopen("calculation.in","r",stdin); freopen("calculation.out","w",stdout); scanf("%lld%lld",&n,&m); for(int i=1;i<=n;i++) scanf("%lld",a+i); build(1,1,n); while(m--){ ch=getchar(); while(ch>'C'||ch<'A') ch=getchar(); if(ch=='A'){ scanf("%d%d%lld%lld",&le,&ri,&k,&b); update(1,1,n); }else if(ch=='B'){ scanf("%d%d",&le,&ri); printf("%lld\n",query1(1,1,n)); }else{ scanf("%d%d",&le,&ri); printf("%lld\n",query2(1,1,n)); } } return 0; }
T3:
#include<iostream> #include<cstdio> #include<cstdlib> #include<cstring> #include<cmath> #include<algorithm> #define ll long long #define maxn 100005 using namespace std; int n,m,T,st[maxn],tp,tot_len; int tot,cirpot[maxn],mx1,mx2; int to[maxn*10],val[maxn*10],ne[maxn*10]; int hd[maxn],dis[maxn],num,ans; bool v[maxn],is_cc[maxn],hhh; inline void init(){ num=ans=tp=tot=tot_len=0; hhh=0; mx1=mx2=0; memset(hd,0,sizeof(hd)); memset(dis,0,sizeof(dis)); memset(is_cc,0,sizeof(is_cc)); memset(v,0,sizeof(v)); } inline void add(int uu,int vv,int ww){ to[++num]=vv,ne[num]=hd[uu],hd[uu]=num,val[num]=ww; to[++num]=uu,ne[num]=hd[vv],hd[vv]=num,val[num]=ww; } void dfs(int x,int len){ ans=max(ans,len); v[x]=1; for(int i=hd[x];i;i=ne[i]) if(!v[to[i]]) dfs(to[i],len+val[i]); v[x]=0; } void tree_dp(int x,int fa){ for(int i=hd[x];i;i=ne[i]) if(to[i]!=fa&&!is_cc[to[i]]){ tree_dp(to[i],x); ans=max(ans,dis[x]+dis[to[i]]+val[i]); dis[x]=max(dis[x],dis[to[i]]+val[i]); } } void find_circle(int x,int fa){ st[++tp]=x,v[x]=1; for(int i=hd[x];i;i=ne[i]) if(to[i]!=fa&&!hhh){ if(v[to[i]]){ hhh=1; int h; for(h=tp;h;h--) if(st[h]==to[i]) break; for(;h<=tp;h++) is_cc[st[h]]=1,cirpot[++tot]=st[h]; } else find_circle(to[i],x); } tp--; } int hh(int x){ if(x==tot+1) return 0; for(int i=hd[cirpot[x]];i;i=ne[i]) if(to[i]==cirpot[x%tot+1]) return val[i]+hh(x+1); return 123445; } void get(int x,int dd){ tree_dp(cirpot[x],0); ans=max(ans,max(dis[cirpot[x]]+mx1+dd,dis[cirpot[x]]+mx2-dd)); mx1=max(mx1,dis[cirpot[x]]-dd); mx2=max(mx2,tot_len+dis[cirpot[x]]+dd); if(x==tot) return; for(int i=hd[cirpot[x]];i;i=ne[i]) if(to[i]==cirpot[x+1]) get(x+1,dd+val[i]); } int main(){ freopen("path.in","r",stdin); freopen("path.out","w",stdout); scanf("%d",&T); for(int l=1;l<=T;l++){ init(); scanf("%d%d",&n,&m); int uu,vv,ww; for(int i=1;i<=m;i++){ scanf("%d%d%d",&uu,&vv,&ww); add(uu,vv,ww); } if(n>=m){ if(n==m+1) tree_dp(1,1); else{ find_circle(1,1); tot_len=hh(1); get(1,0); } }else{ for(int i=1;i<=n;i++) dfs(i,0); } printf("%d\n",ans); } return 0; }
T3竟然是找环之后单调队列????
代码难度->INF
(神TM仙人掌,这个坑回来一定要填)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号