一道神秘题

 

 

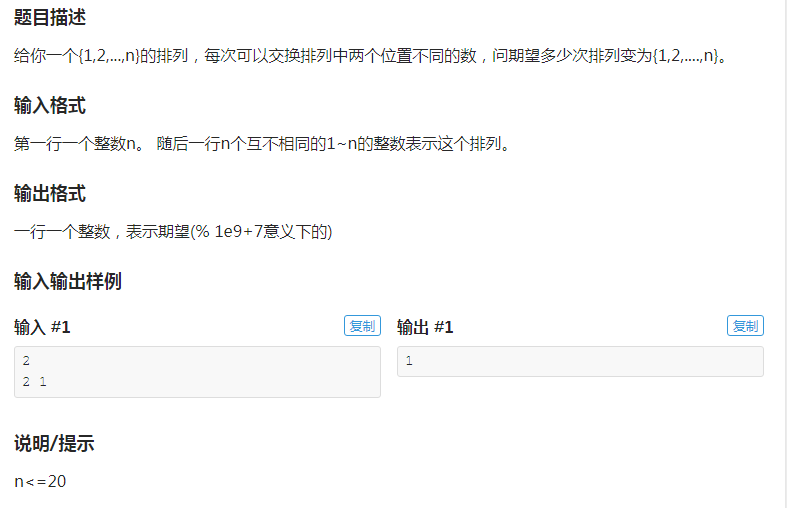
当然这里不会透露题目来源

 

 

好的，现在来正经讲题。

一看到n<=20，首先反应肯定是状压之类的，不过目测 n<=20只能用二进制表示吧？？？

 

然而二进制一点也不会解呢。。。。换个思路。

 

 

首先这种不能直接算期望的题一般都要设状态，然后通过状态间的转移算出每个状态的期望。如果状态间是dag，那么就可以开心dp；否则只能高斯消元？(类似随机游走)

然后看一下这个题，发现如果把每种排列当成一个状态显然会爆炸，而且状态间必然不是DAG，所以应该是要高斯消元的，所以我们只能把状态数限制在 O(状态数^3)能过的数量级。

再考虑一下，排列通常可以表示成图中的若干简单环，那么是不是每两种 在对应的图中由每个简单环大小构成的集合(无序)相同的 排列 (对于这个题来说) 是等价的？

等我接下来讲一下交换两个数对于图的影响，你们就能想明白了。。。

 

画图就可以发现：

    1.如果交换两个不在一个环中的数，结果是新图中两个环合并了。

    2.如果交换两个在一个环中的数，结果是新图中这个环分裂了。

 

而且根据对称性，环分裂的每种情况是等概率的(这个会在后面构造矩阵系数的时候用到)。

 

于是我们惊奇的发现： 每个排列只有它对应的图中的每个简单环大小构成的集合(无序)是有用的信息，我们把它作为状态即可。

 

然后让我们算一下总状态数：显然它是一个整数划分。然后我写了个整数划分算了一下不到700。。。

但为什么 O（N^3）的高斯消元能过呢。。。。我也不知道。。。(好像高斯消元的常数就是小)

 

关于一些详细的东西，比如状态转移还有状态存储之类的，就交给你们啦hhhh，想不明白可以参考我代码w

 

 

#include<cstdio>
#include<cstdlib>
#include<vector>
#include<algorithm>
#include<unordered_map>
#define ll long long
using namespace std;
#define pb push_back
const int N=701,ha=1e9+7;

inline int add(int x,int y){ x+=y; return x>=ha?x-ha:x;}
inline void ADD(int &x,int y){ x+=y; if(x>=ha) x-=ha;}

inline int ksm(int x,int y){
	int an=1;
	for(;y;y>>=1,x=x*(ll)x%ha) if(y&1) an=an*(ll)x%ha;
	return an;
}

vector<int> g[N];
unordered_map<int,int> mmp;
int a[N][N],n,p[N],b[N],num,k,pos,inv;
bool v[N];

inline int Get(vector<int> u){
	int now=0;
	for(int i:u) now=now*29+i;
	return now;
}

inline void update(int len){
	k++;
	for(int i=1;i<=len;i++) g[k].pb(b[i]);
	mmp[Get(g[k])]=k;
}

void dfs(int x,int y,int lef){
	b[x]=y;
	if(!lef) update(x);
	for(int i=lef;i>=y;i--) dfs(x+1,i,lef-i);
}

inline void sc(int x){
	int tt;
	for(tt=0;!v[x];x=p[x]) tt++,v[x]=1;
	b[++num]=tt;
}

inline void Find(int x){
	int m=g[x].size();
	vector<int> o;
	
	for(int i=0,P,Q;i<m;i++){
		P=g[x][i];
	    for(int j=i+1;j<m;j++){
	    	Q=g[x][j];
	    	o.clear();
	    	for(int w=0;w<m;w++) if(w!=i&&w!=j) o.pb(g[x][w]);
	    	o.pb(P+Q),sort(o.begin(),o.end());
	    	ADD(a[x][mmp[Get(o)]],P*Q*2);
	    }
	}
	
	for(int i=0,P;i<m;i++){
		P=g[x][i];
		for(int j=1;j<P;j++){
			o.clear();
			for(int l=0;l<m;l++) if(l!=i) o.pb(g[x][l]);
			o.pb(j),o.pb(P-j),sort(o.begin(),o.end());
			ADD(a[x][mmp[Get(o)]],P%ha);
		}
	}
	
	for(int i=1;i<k;i++) a[x][i]=(ha-a[x][i])*(ll)inv%ha;
	a[x][x]=1,a[x][k]=1;
}

inline void build(){
	for(int i=1;i<=n;i++) if(!v[i]) sc(i);
	sort(b+1,b+num+1);
	vector<int> o;
	for(int i=1;i<=num;i++) o.pb(b[i]);
	pos=mmp[Get(o)];
	
	for(int i=1;i<k;i++) Find(i);
}

inline void solve(){
	for(int i=1,o;i<k;i++){
        for(o=i;o<k&&!a[o][i];o++);
        if(o>i) for(int j=i;j<=k;j++) swap(a[i][j],a[o][j]);
        
        int INV=ksm(a[i][i],ha-2),tmp;
        for(int j=i+1;j<k;j++) if(a[j][i]){
        	tmp=INV*(ll)a[j][i]%ha;
        	for(int l=i;l<=k;l++) ADD(a[j][l],ha-a[i][l]*(ll)tmp%ha);
		}
	}
	
	for(int i=k-1;i;i--){
		for(int j=i+1;j<k;j++) ADD(a[i][k],ha-a[i][j]*(ll)a[j][k]%ha);
		a[i][k]=a[i][k]*(ll)ksm(a[i][i],ha-2)%ha;
	}
}

int main(){	
//    freopen("one.in","r",stdin);
//    freopen("one.out","w",stdout);

	scanf("%d",&n),inv=ksm(n*(n-1),ha-2);
	for(int i=1;i<=n;i++) scanf("%d",p+i);
	
	dfs(0,1,n);

	build();

/*
	for(int i=1;i<k;i++){
	    for(int j=1;j<=k;j++) printf("%d ",a[i][j]);
	    puts("");
	}
*/
	
	solve();
	
	printf("%d\n",a[pos][k]);
	return 0;
}