图-实验报告

图-实验报告

代码托管地址

实验-1

实验要求

用邻接矩阵实现无向图（边和顶点都要保存），实现在包含添加和删除结点的方法，添加和删除边的方法，size(),isEmpty()，广度优先迭代器，深度优先迭代器

实验步骤

1，成员变量，构造函数，以及数组扩展

实现策略：维护一个顶点的数组，以及一个二维的数组来表示顶点之间的关系，维护2个基本变量记录顶点和边的数量。

重点是：
1）可以动态扩展顶点数组，并保持数组的连续性，这意味着删除顶点时后面的顶点要前移，那么顶点的编号也变了，关系矩阵也要改变。　　　　
2）关系矩阵也动态维护，随时保持和顶点数组一样大。顶点数组的长度为VNodes.length，实际存放了顶点的位置只到了size()处，对应的，关系矩阵的大小为int[VNodes.length][VNodes.length]，实际有效地区域也只在左上角的int[size()][size()]范围内。

2，建图，删图相关方法分析

1）添加边，只需要在关系矩阵M的两个位置上赋值即可，而在邻接表实现中，要在2个顶点的边链表的最后都添加上一个边

2）删除边，1）的逆过程，将那2个位置的值置为0即可，而在邻接表的实现中，也是要到边链表中去删（还要记录被删边得前缀）

3）添加顶点，直接在顶点数组中添加一个，注意如果满的话，要扩展，在扩展方法中，已经实现了同时扩展关系矩阵（将矩阵变大了，左上角有效区域还是不变）。在邻接表中这个稍微简单点，因为邻接表直接扩展数组即可，关系不用动。

4）删除顶点，无论哪种方式，删除顶点都是最麻烦的，在邻接表的实现中，删除顶点要先删除所有跟顶点关联的边，然后后面的顶点前移以保证顶点数组连续，移动会导致原来的顶点的边链表的信息变化（边的端点），所以在移动前先将所有边链表中的边得信息调整好，再来移动数组使它保持连续。

3，广度优先遍历和深度优先遍历

拿广度优先遍历来说，顶点A每次从遍历队列出来的时候要将其未被访问的关联顶点添加到遍历队列，这就需要求得A在顶点数组里的位置，然后在关系矩阵里找跟它关联且没有被访问的顶点。

深度优先的实现只需要把遍历队列改成遍历栈即可。

实验问题及解决

问题1

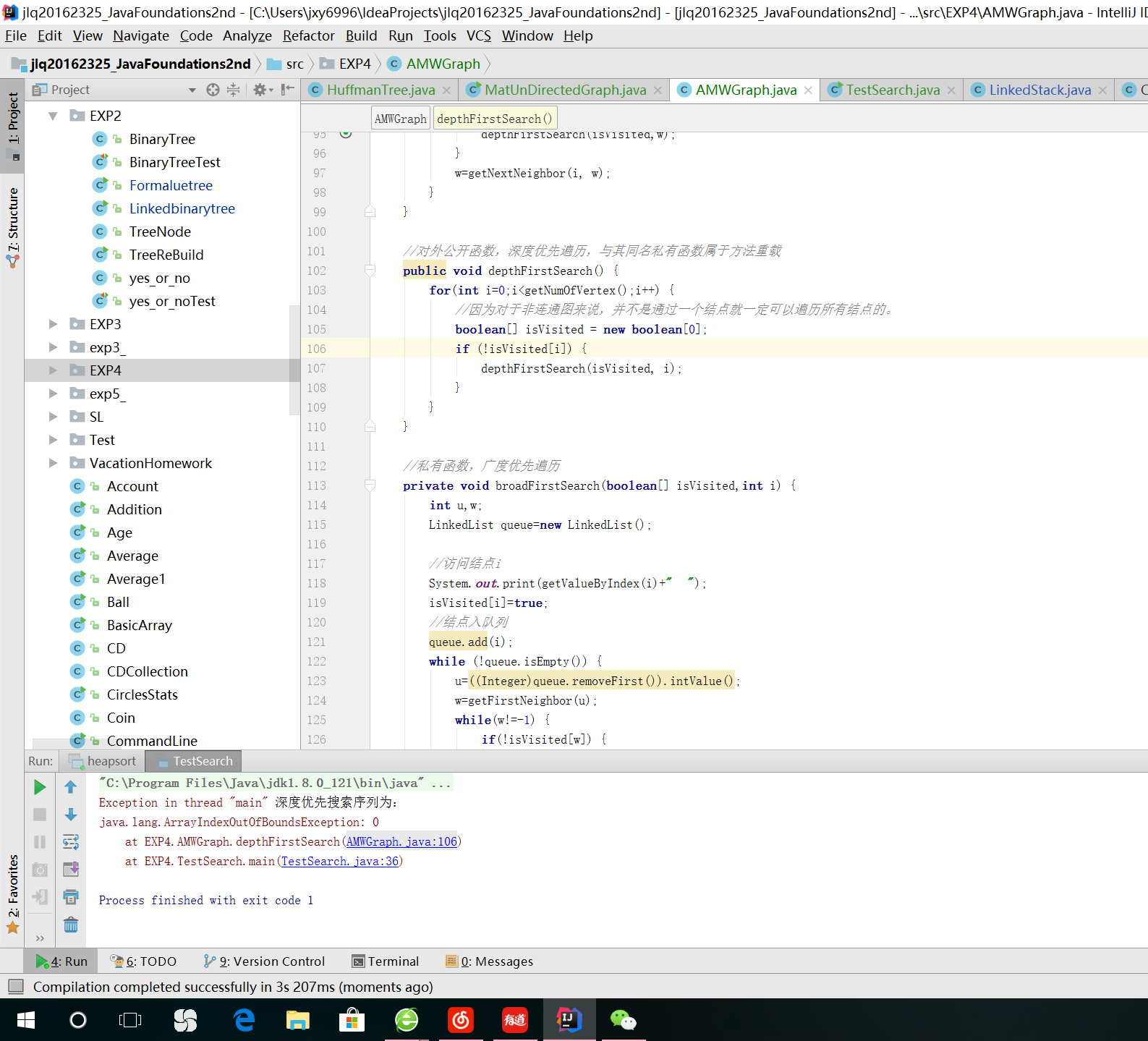
  • 方案

  • 解决结果

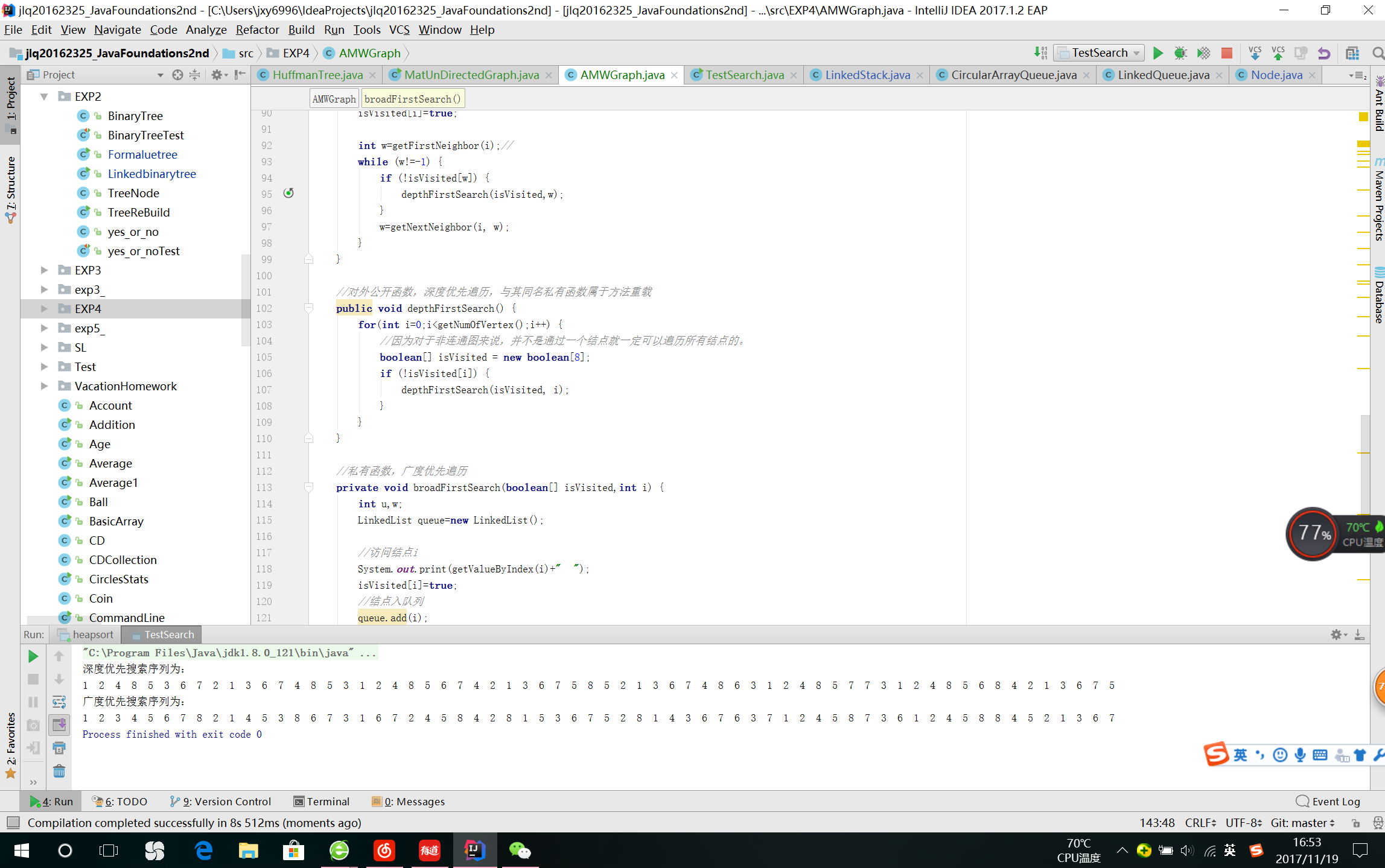
问题2

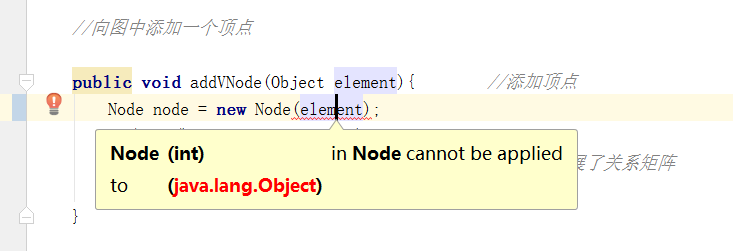
  • 解决措施

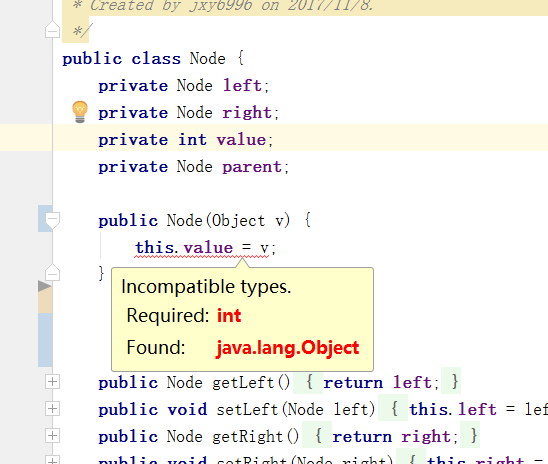
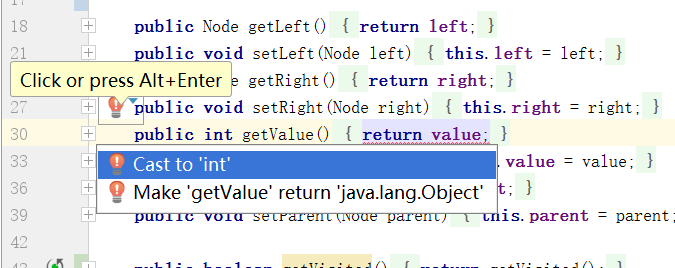
测试结果

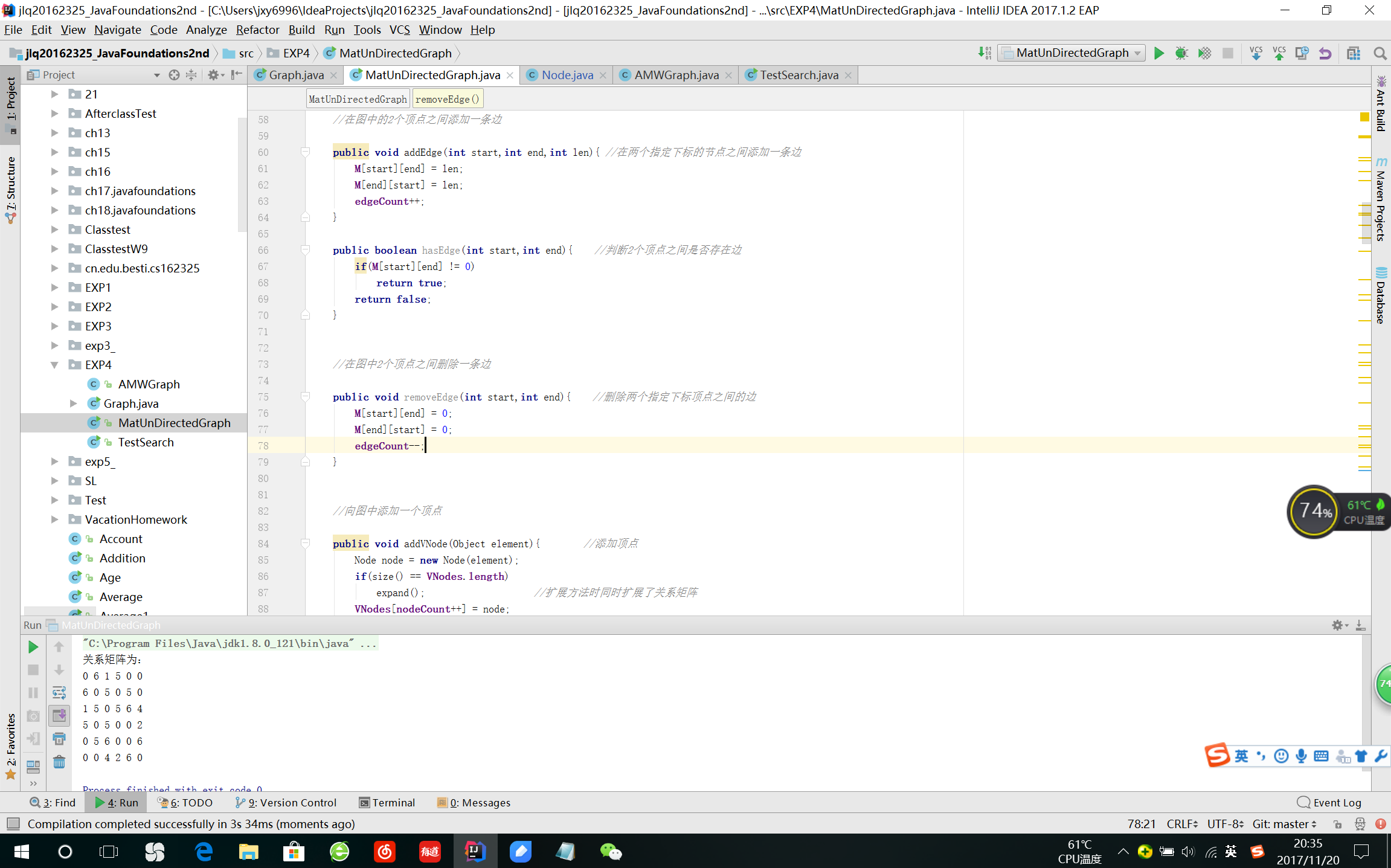
实验-2

实验要求

用十字链表实现无向图（边和顶点都要保存），实现在包含添加和删除结点的方法，添加和删除边的方法，size(),isEmpty()，广度优先迭代器，深度优先迭代器

实验问题

  • 在查阅十字链表的概念时，看到“十字链表（Orthogonal List)是有向图的另一种 链式存储结构 。该结构可以看成是将有向图的 邻接表 和逆邻接表结合起来得到的。”
    并参考十字链表是无向图的一种存储结构()_牛客网验证题目有误。

  • 但也有同学称“无向图是特殊的有向图”。

实验知识点

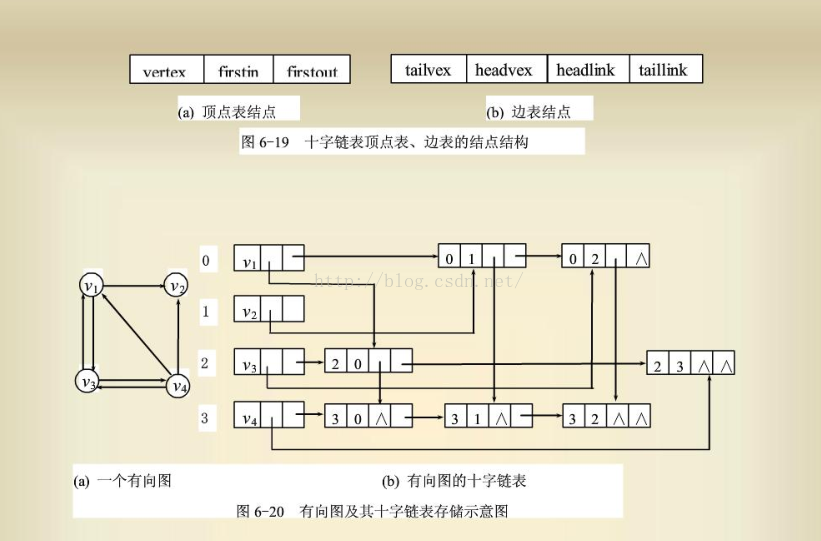
其中

firstIn表示入边表头指针，指向该顶点的入边表中第一个结点，
firstOut表示出边表头指针，指向该顶点的出边表中的第一个结点。

tailvex是指弧起点在顶点表的下标，
headvex是弧终点在顶点表的下标，
headlink是指入边表指针域，指向终点相同的下一条边，
tailvex是指边表指针域，指向起点相同的下一条边。

测试结果


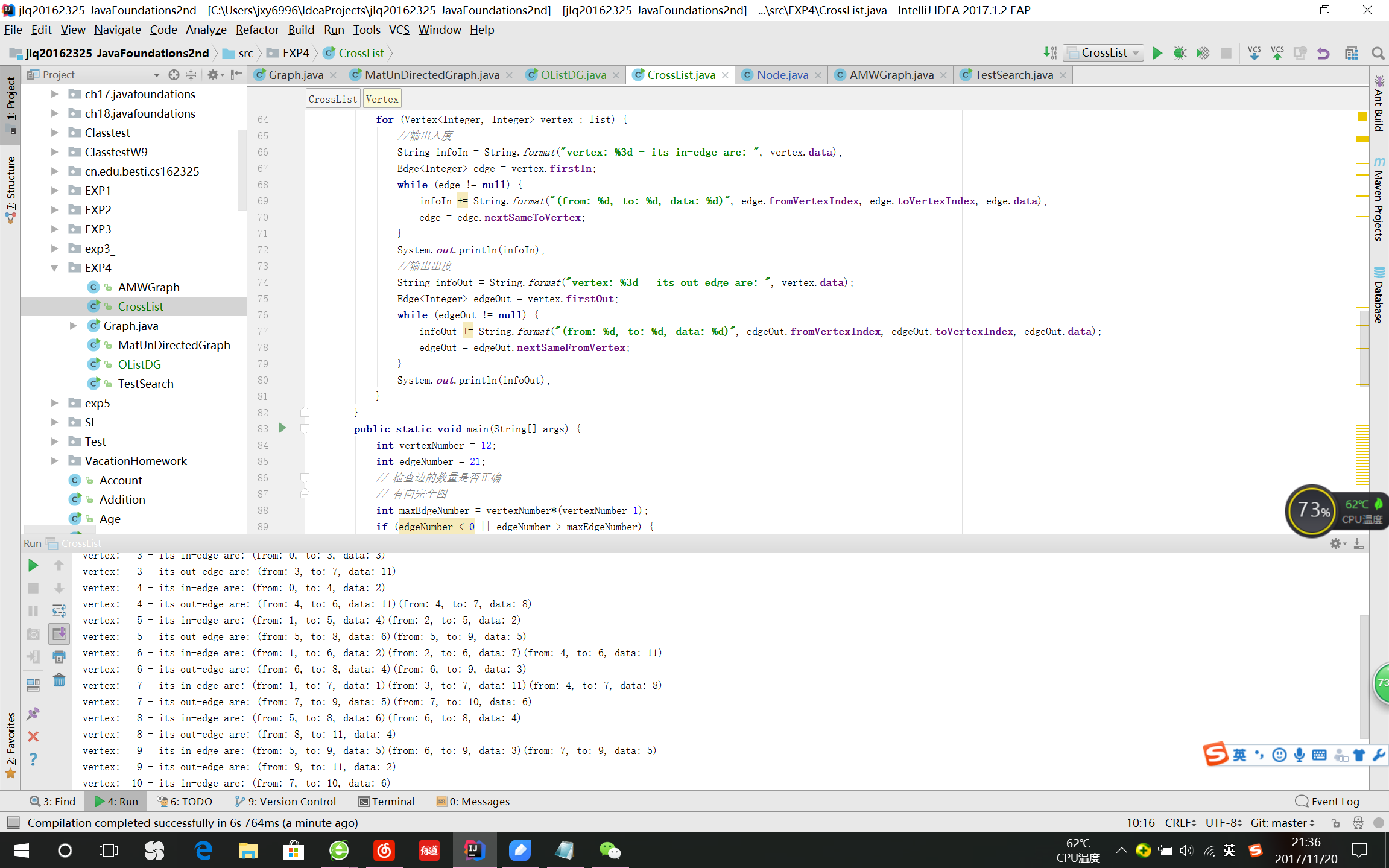
实验-3

实验要求

实现PP19.9——创建计算机网络路由系统，输入网络中点到点的线路，以及每条线路使用的费用，系统输出网络中各点之间最便宜的路径，指出不相通的位置。

实验知识点

用一个带权的图来表示一个网络。用图的顶表示地点，用图中的边表示两地之间的信息路线，每条边上所附的权值表示该路线的长度。 dist[][]数组初始化为各顶点间的原本距离，最后存储各顶点间的最短距离。 path[][]数组保存最短路径，与当前迭代的次数有关。初始化都为-1，表示没有中间顶点。在求dist[i][j]过程中，path[i][j]存放从顶点vi到顶点vj的中间顶点编号不大于k的最短路径上前一个结点的编号。在算法结束时，由二维数组path的值回溯，可以得到从顶点vi到顶点vj的最短路径。

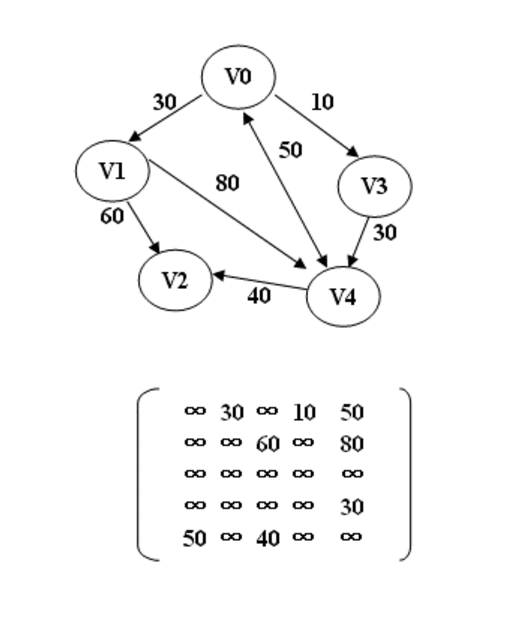
测试结果

实验总结

  • 遇到问题不再像以前那么焦虑不知所措，能静下心来，查找解决措施，并尝试解决，顺利时就很开心。

参考链接

posted @ 2017-11-22 17:00  20162325金立清  阅读(562)  评论(0)  编辑  收藏  举报