20162325 金立清 S2 W10 C19
20162325 2017-2018-2 《程序设计与数据结构》第10周学习总结
认识
- 线性表和树两类数据结构,线性表中的元素是“一对一”的关系,树中的元素是“一对多”的关系,本章所述的图结构中的元素则是“多对多”的关系。图(Graph)是一种复杂的非线性结构,在图结构中,每个元素都可以有零个或多个前驱,也可以有零个或多个后继,也就是说,元素之间的关系是任意的。
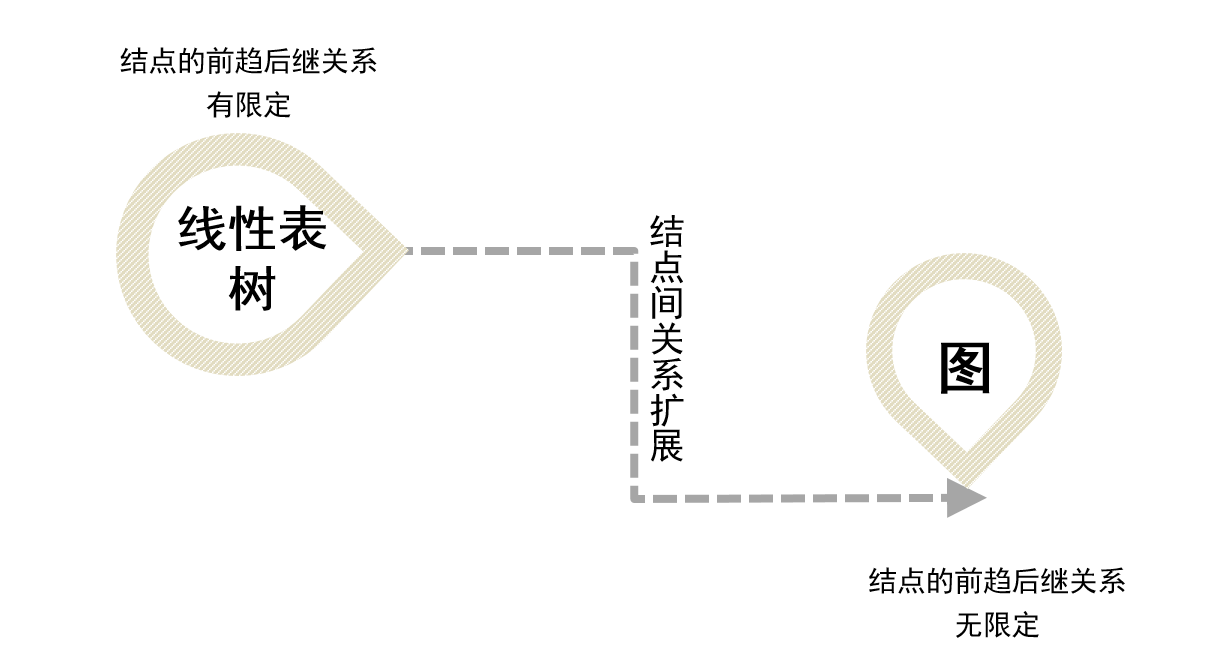
图的基本概念
1. 图的定义
定义:图(graph)是由一些点(vertex)和这些点之间的连线(edge)所组成的;其中,点通常被成为"顶点(vertex)",而点与点之间的连线则被成为"边或弧"(edege)。

2. 图的种类
根据边是否有方向,将图可以划分为:无向图和有向图。
2.1 无向图

2.2 有向图
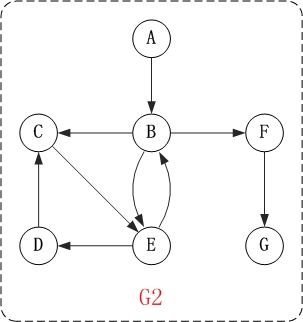
3. 邻接点和度
3.1 邻接点
- 一条边上的两个顶点叫做邻接点。
- 例如,上面无向图G0中的顶点A和顶点C就是邻接点。
有向图:如果<u, v>∈ E, 则称v为u的邻接点,u为v的逆邻接点。边<u, v>与顶点u和v相关联,从u出发的边称为u的出边或邻接边,而指向顶点u的边称为u的入边或逆邻接边。
无向图:如果(u, v)∈ E, 则称u与v互为邻接点。
3.2 顶点的度、入度与出度
- 在无向图中,某个顶点的度是邻接到该顶点的边(或弧)的数目,出度入度相等。
- 例如,上面无向图G0中顶点A的度是2。
在有向图中,顶点v的 入度: 指以顶点为终点的边的数目。 出度:指以顶点起始点的边的数目; 顶点的度=入度+出度。 例如,上面有向图G2中,顶点B的入度是2,出度是3;顶点B的度=2+3=5。
4. 路径和回路
路径:如果顶点(Vm)到顶点(Vn)之间存在一个顶点序列。则表示Vm到Vn是一条路径。
路径长度:路径中"边或弧的数量"。
简单路径:若一条路径上顶点不重复出现,则是简单路径。
回路:若路径的第一个顶点和最后一个顶点相同,则是回路。
简单回路:第一个顶点和最后一个顶点相同,其它各顶点都不重复的回路则是简单回路。
5. 连通图和连通分量
-
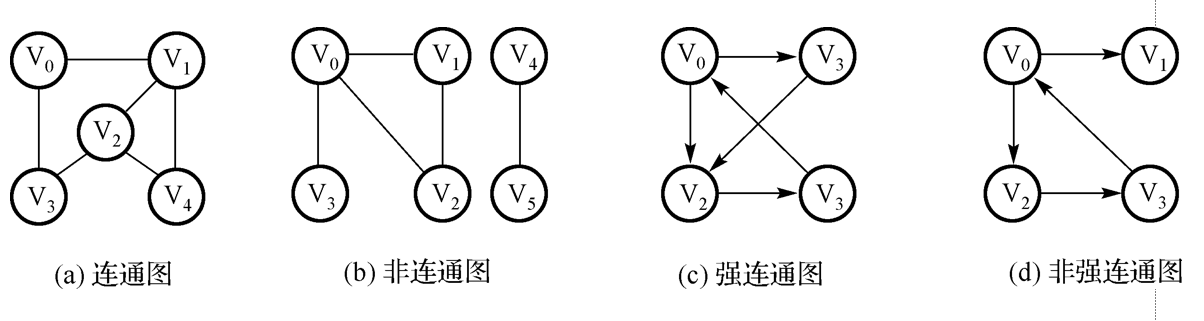
连通图:无向图中,若一个顶点到另一个顶点有路径,则称这两个顶点是连通的。如果图中任意两个顶点都是连通的,则称该图是连通图。 有向的连通图称为强连通图。
![]()
-
连通分量:非连通图中的各个连通子图称为该图的连通分量。
6. 权
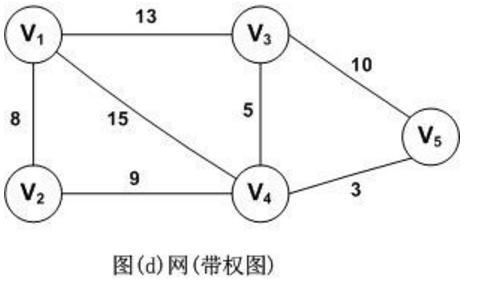
- 图的边和弧上相关的数,叫做权(Weight)。这些带权的图通常称为网(Network)。
![]()
图的存储结构
- 图的结构比价复杂,任意两个顶点之间都可能存在关系,不能用简单的顺序存储结构来表示。如果运用多重链表,即一个数据域多个指针域组成的结点表示图中一个结点,则造成大量存储单元浪费。图的存储结构,常用的是"邻接矩阵"和"邻接表",此外还有"十字链表"。
1. 邻接矩阵
- 邻接矩阵是指用矩阵来表示图。它是采用矩阵来描述图中顶点之间的关系(及弧或边的权)。
假设图中顶点数为n,则邻接矩阵定义为:
![]()

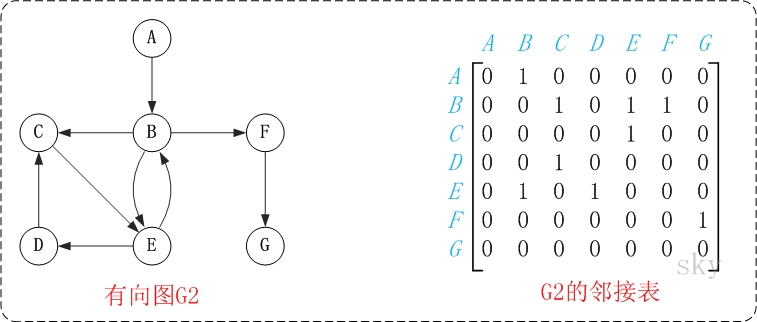
- 通常采用两个数组来实现邻接矩阵:一个一维数组用来保存顶点信息,一个二维数组来用保存边的信息。

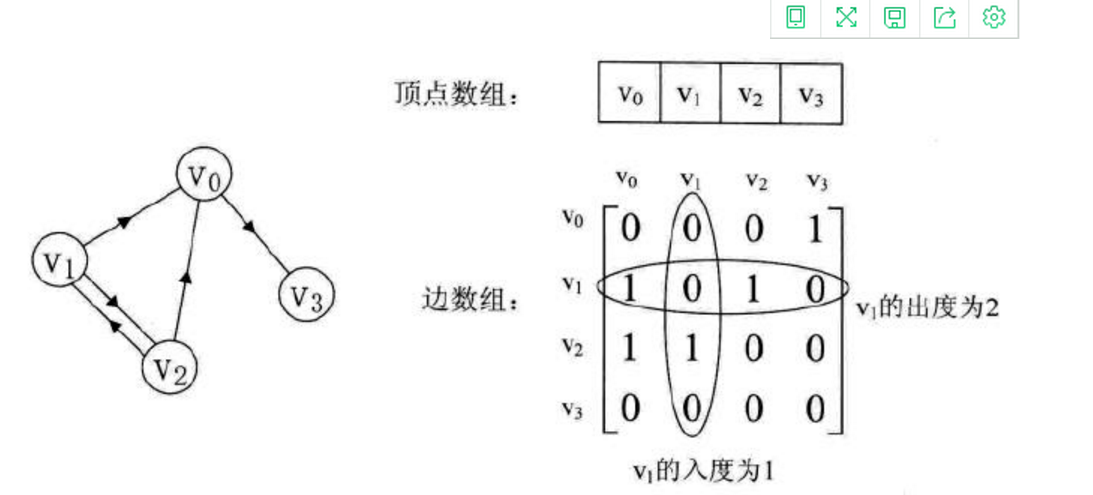

- 邻接矩阵具有以下特点:
a)邻接矩阵是正矩阵,即横纵维数相等。
b)矩阵的每一行或一列代表一个顶点,行与列的交点对应这两个顶点的边。
c)矩阵的点代表边的属性,1代表有边,0代表无边,所以矩阵的对角线都是0,因为对角线上对应的横纵轴代表相同的顶点,边没有意义。
d)如果是无向图,那么矩阵是对称矩阵,也一定是对称矩阵(主对角线(左上到右下)相等);如果是有向图则不一定。
e)如果是有权图,矩阵点数值可以是权值。
f)邻接矩阵表示图的关系非常清晰,但消耗空间较大。
2. 邻接表
-
对于边相对与定点较少的图,邻接矩阵表示很浪费空间
![]()
-
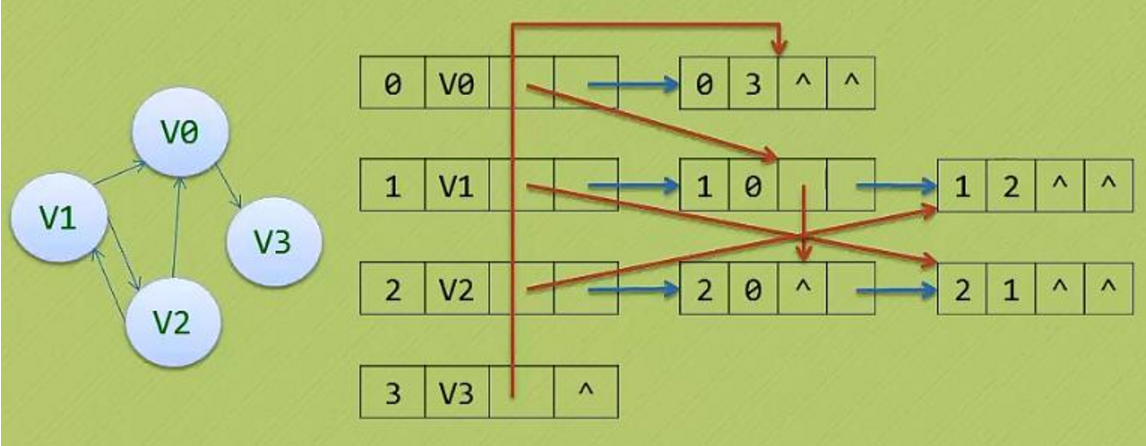
邻接表是图的一种链式存储表示方法,以一组链表来表示顶点间关系,它是改进后的"邻接矩阵"。
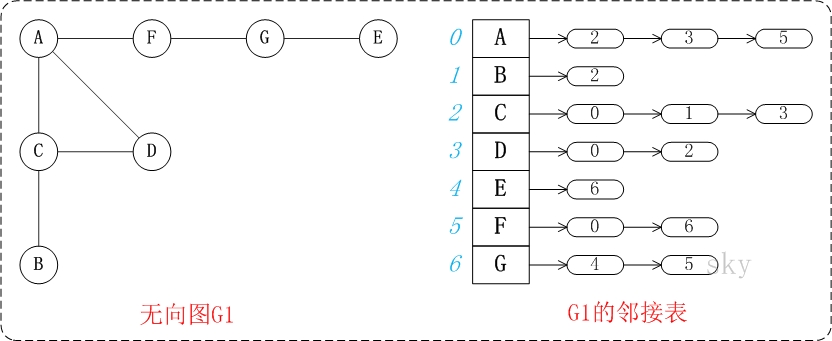
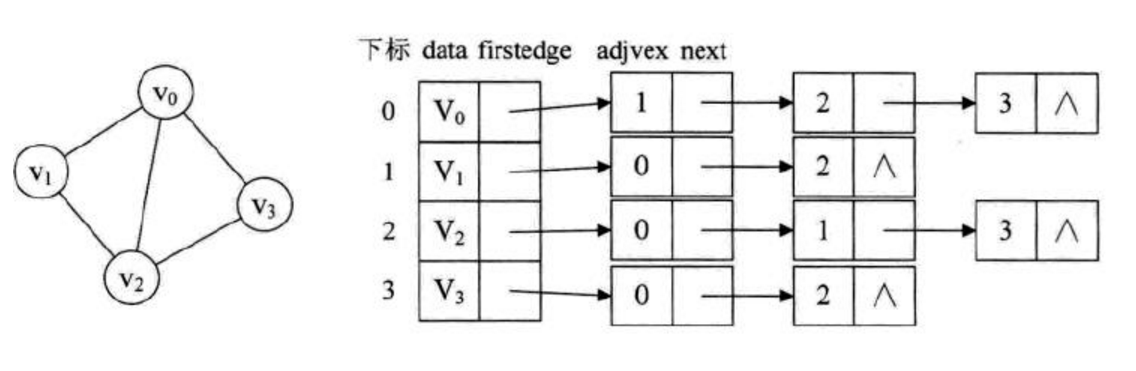
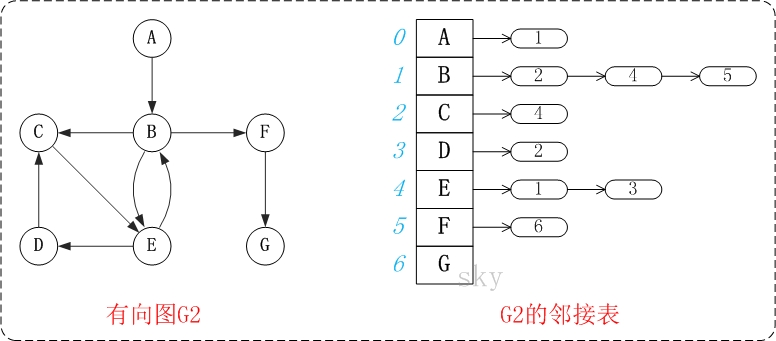
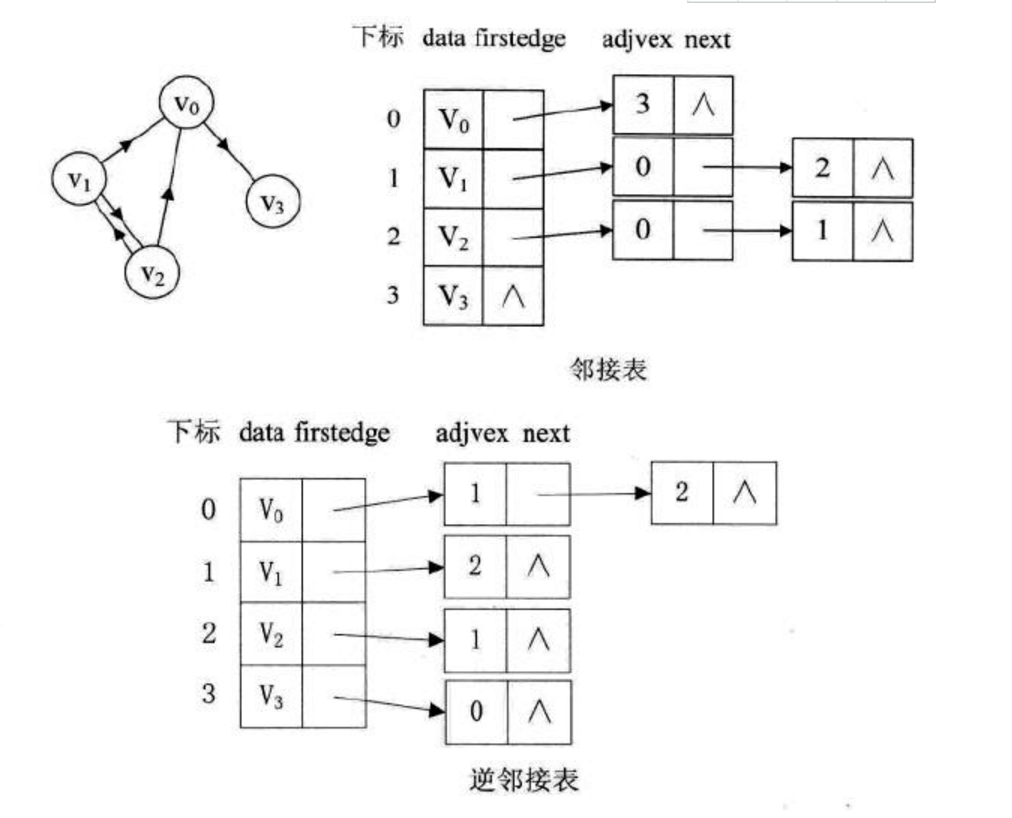
-
一个有向图的逆邻接表,就是对每个顶点vi都建议一个链接为vi为弧头的表。
-
邻接表具有以下特点:
a)邻接表示一个有但链表组成的数组。
b)图中的每一个顶点都有一个链,数组的大小等于图中顶点的个数。
c)无向图的链的第一个元素是本顶点,后继分别连接着和这个顶点相连的顶点;有向图的链第一个顶点是本顶点,后继是以本顶点为起点的边的终点。
如果是有权图,可以在节点元素中设置权值属性。
d)邻接链表关系表示不如邻接矩阵清晰,不方便判断两个顶点之间是否有边,但节省空间。
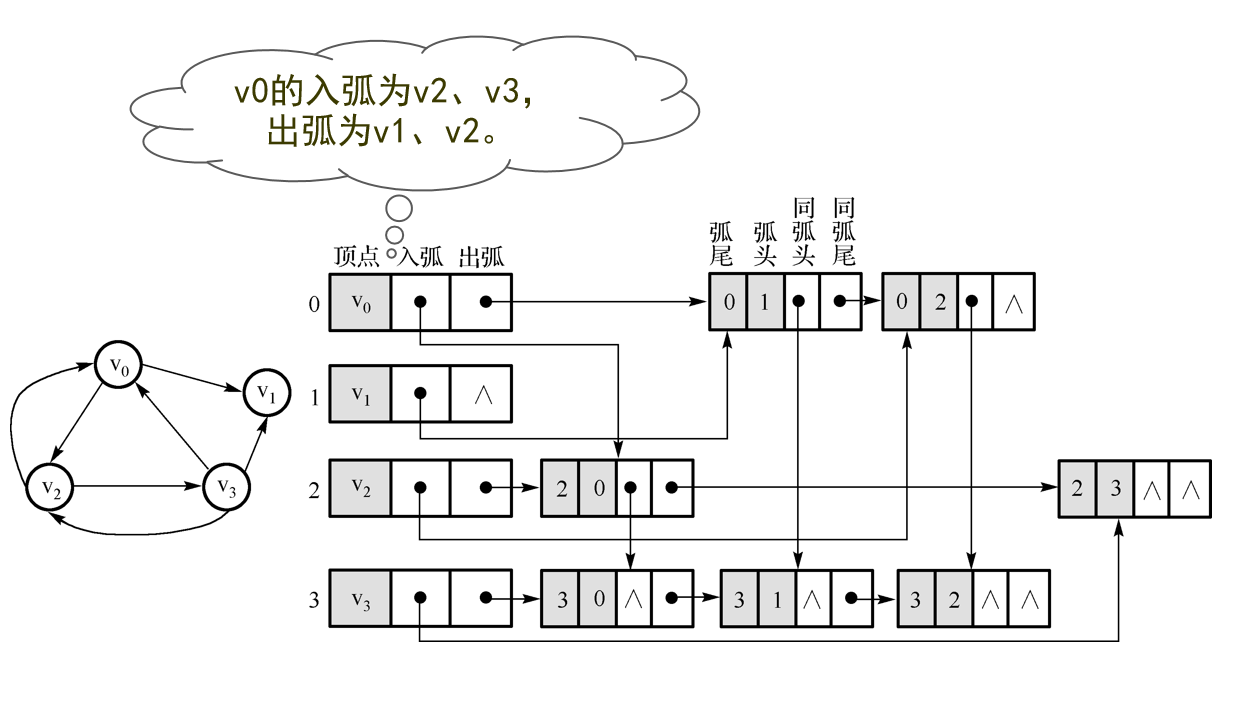
十字链表
- 顶点表结点结构:
![]()
firstin:表示入边表头指针,指向该顶点的入边表中第一个结点。
firstout:表示出边表头指针,指向该顶点的出边表中的第一个结点。
- 边表结点结构:
![]()
tailvex:指弧起点在顶点表的下标。
headvex:指弧终点在顶点表中的下标。
headlink:指入边表指针域。
taillink:指边表指针域。
- 如果是网,还可以再增加一个weight域来存储权值。
![]()
图的遍历
- 深度优先搜索遍历(栈)
深度优先搜索DFS遍历类似于树的前序遍历。其基本思路是:
a) 假设初始状态是图中所有顶点都未曾访问过,则可从图G中任意一顶点v为初始出发点,首先访问出发点v,并将其标记为已访问过。
b) 然后依次从v出发搜索v的每个邻接点w,若w未曾访问过,则以w作为新的出发点出发,继续进行深度优先遍历,直到图中所有和v有路径相通的顶点都被访问到。
c) 若此时图中仍有顶点未被访问,则另选一个未曾访问的顶点作为起点,重复上述步骤,直到图中所有顶点都被访问到为止。
图示如下:
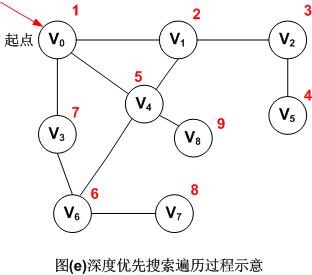
注:红色数字代表遍历的先后顺序,所以图(e)无向图的深度优先遍历的顶点访问序列为:V0,V1,V2,V5,V4,V6,V3,V7,V8
如果采用邻接矩阵存储,则时间复杂度为O(n2);当采用邻接表时时间复杂度为O(n+e)。
- 广度优先搜索遍历(队列)
广度优先搜索遍历BFS类似于树的按层次遍历。其基本思路是:
a) 首先访问出发点Vi
b) 接着依次访问Vi的所有未被访问过的邻接点Vi1,Vi2,Vi3,…,Vit并均标记为已访问过。
c) 然后再按照Vi1,Vi2,… ,Vit的次序,访问每一个顶点的所有未曾访问过的顶点并均标记为已访问过,依此类推,直到图中所有和初始出发点Vi有路径相通的顶点都被访问过为止。
图示如下:
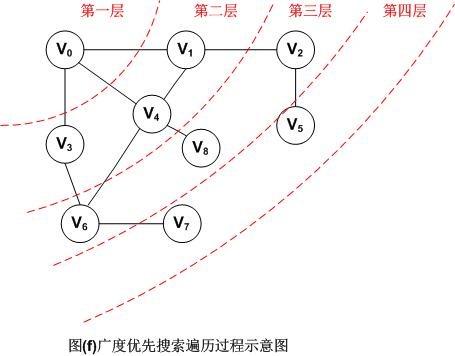
因此,图(f)采用广义优先搜索遍历以V0为出发点的顶点序列为:V0,V1,V3,V4,V2,V6,V8,V5,V7
如果采用邻接矩阵存储,则时间复杂度为O(n2),若采用邻接表,则时间复杂度为O(n+e)。
最小生成树和最短路径
1,最小生成树
在弄清什么是最小生成树之前,我们需要弄清什么是生成树?
用一句语简单概括生成树就是:生成树是将图中所有顶点以最少的边连通的子图。
比如图(g)可以同时得到两个生成树图(h)和图(i)
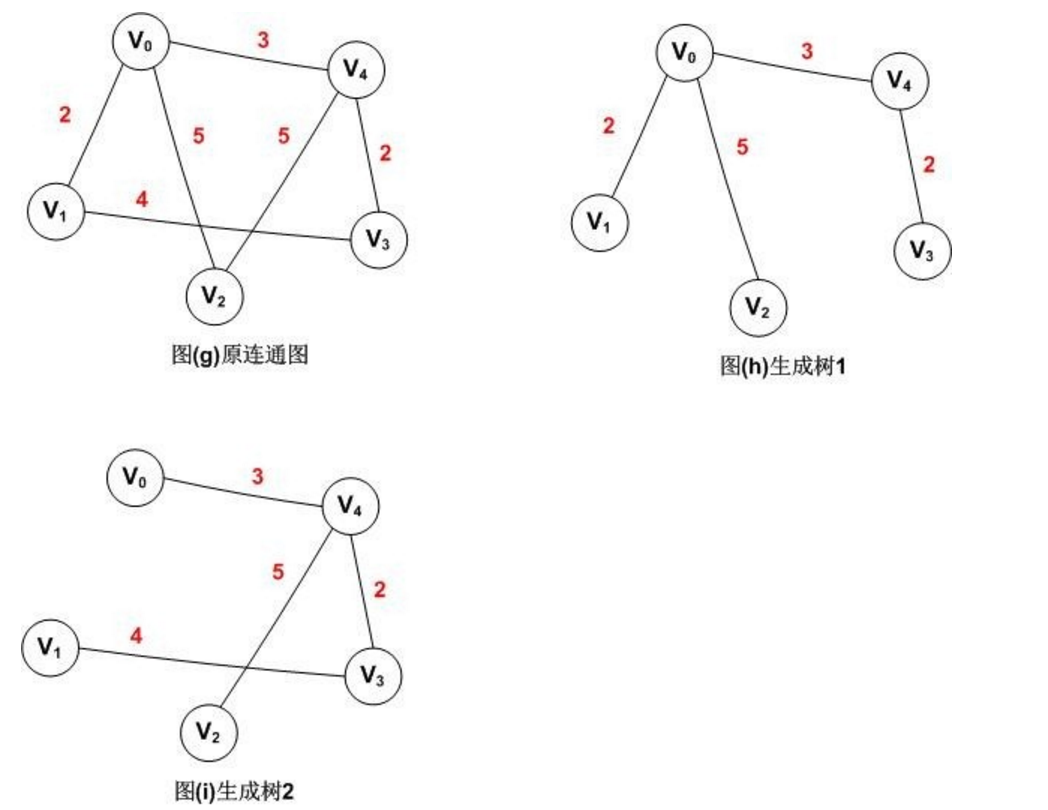
那所谓最小生成树,用一句话总结就是:权值和最小的生成树就是最小生成树。
比如上图中的两个生成树,生成树1和生成树2,生成树1的权值和为:12,生成树2的权值为:14,我们可以证明图(h)生成树1就是图(g)的最小生成树。
如何构造最小生成树呢?可以使用普里姆算法——参见数据结构与算法--图 - CSDN博客
2,最短路径
求最短路径也就是求最短路径长度。下面是一个带权值的有向图,表格中分别列出了顶点V1其它各顶点的最短路径长度。
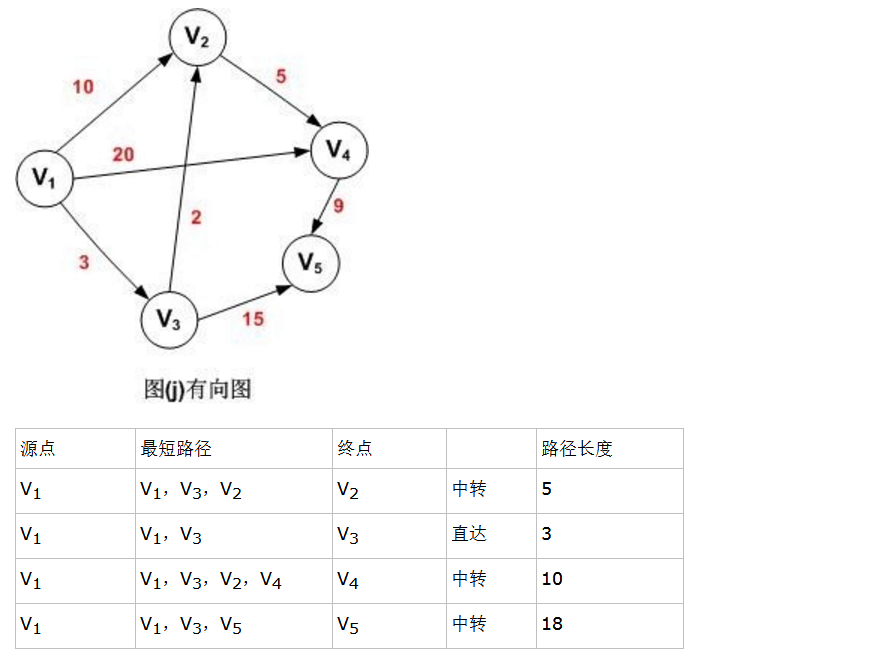
表:顶点V1到其它各顶点的最短路径表
从图中可以看出,顶点V1到V4的路径有3条(V1,V2,V4),(V1,V4),(V1,V3,V2,V4),其路径长度分别为15,20和10,因此,V1到V4的最短路径为(V1,V3,V2,V4)。
如何求带权有向图的最短路径长度呢?可以使用迪杰斯特拉算法——同样参见数据结构与算法--图 - CSDN博客
教材学习中的问题和解决过程
-
问题1:书上P423页说道“用邻接矩阵表示带权图,用矩阵中的每个位置表示边的权就可以”,不明白是怎么表示的。
-
问题1解决方案:上网查找答案,参考java 图的邻接矩阵
-
问题2:邻接矩阵与邻接表的比较?
-
问题2解决方案:
当图中结点数目较小且边较多时,采用邻接矩阵效率更高。
当节点数目远大且边的数目远小于相同结点的完全图的边数时,采用邻接表存储结构更有效率。
代码调试中的问题和解决过程
- 这周主要代码在实验部分,请见实验博客
代码托管
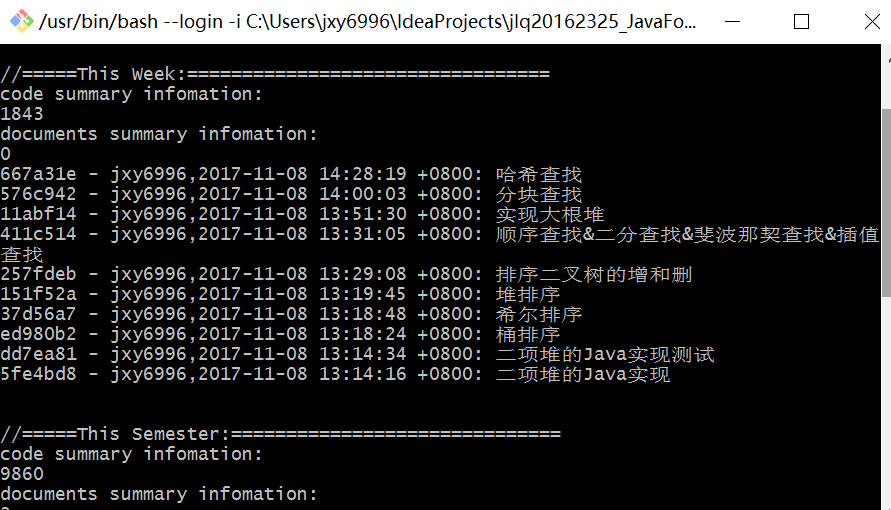
上周考试错题总结
-
![]()
![]()
-
解答:解析和答案相符,可能是系统出错?
-
-
解答:
![]()
-
![]()
-
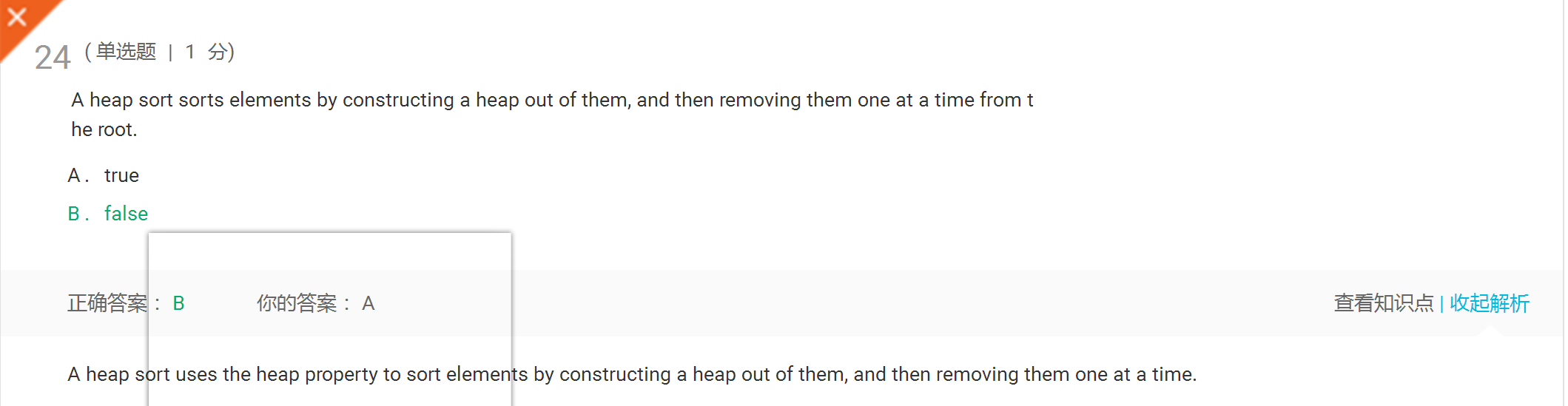
解答:是删除堆,不是从根目录
本周结对学习情况
- 结对搭档
- 结对学习内容
- 蓝墨测试题
其他(感悟、思考等,可选)
- 这周的主要任务是实验三,小部分实验内容是以前做过的,更多是在之前的基础上结合后面学到的知识加以拓展应用。这学期的团队项目快要正式拉开帷幕了,还是有一点紧张,但相信在和队友的通力合作下,我们组的成果会令人满意的!
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 5000行 | 30篇 | 400小时 | |
| 第一周 | 58/ | 1/1 | 10/10 | |
| 第二周 | 8/18 | |||
| 第三周 | 134/ | 3/4 | 12/ 30 | |
| 第四周 | 2/6 | 12/42 | ||
| 第五&六周 | 750/ 6595 | 5/11 | 24/66 | |
| 第七周 | 764/7068 | 7/13 | 18/84 | |
| 第八周 | 888/7956 | 9/15 | 20/104 | |
| 第九周 | 475/8431 | 12/18 | 22/126 | |
| 第十周 | 1429/9860 | 16/22 | 24/150 |
-
计划学习时间: 24小时
-
实际学习时间: 24小时
-
改进情况:只是想吐槽一下……每周要写的博客真多









 浙公网安备 33010602011771号
浙公网安备 33010602011771号