20162325 结对编程项目-四则运算 整体总结
20162325 结对编程项目-四则运算 整体总结
一、需求分析
- 支持多运算符
- 支持真分数
- 用户可选择生成题目的等级
- 处理生成题目并输出到文件
- 完成题目后从文件读入并判题
二、设计思路
这周任务是试着完成上周的拓展内容。1、增加真分数。修改Operad类中的getOp1和getOp2方法,使其随机生成整数或真分数。2、支持多运算符,新建一个MakeQuestions类。3、将原来含有main函数的类分为两个,OutInputQuestionsToFile和OutputResultToFile。
UML类图
三、实现过程中的关键代码
- 支持真分数
package Arithmetic;
/**
* Created by Administrator on 2017/5/15.
*/
//********************************************************************
// RationalNumber.java Java Foundations
//
// Represents one rational number with a numerator and denominator.
//********************************************************************
public class RationalNumber
{
private int numerator, denominator;
//-----------------------------------------------------------------
// Constructor: Sets up the rational number by ensuring a nonzero
// denominator and making only the numerator signed.
//-----------------------------------------------------------------
public RationalNumber (int numer, int denom)
{
if (denom == 0)
denom = 1;
// Make the numerator "store" the sign
if (denom < 0)
{
numer = numer * -1;
denom = denom * -1;
}
numerator = numer;
denominator = denom;
reduce();
}
//-----------------------------------------------------------------
// Returns the numerator of this rational number.
//-----------------------------------------------------------------
public int getNumerator ()
{
return numerator;
}
//-----------------------------------------------------------------
// Returns the denominator of this rational number.
//-----------------------------------------------------------------
public int getDenominator ()
{
return denominator;
}
//-----------------------------------------------------------------
// Returns the reciprocal of this rational number.
//-----------------------------------------------------------------
public RationalNumber reciprocal ()
{
return new RationalNumber (denominator, numerator);
}
//-----------------------------------------------------------------
// Adds this rational number to the one passed as a parameter.
// A common denominator is found by multiplying the individual
// denominators.
//-----------------------------------------------------------------
public RationalNumber add (RationalNumber op2)
{
int commonDenominator = denominator * op2.getDenominator();
int numerator1 = numerator * op2.getDenominator();
int numerator2 = op2.getNumerator() * denominator;
int sum = numerator1 + numerator2;
return new RationalNumber (sum, commonDenominator);
}
//-----------------------------------------------------------------
// Subtracts the rational number passed as a parameter from this
// rational number.
//-----------------------------------------------------------------
public RationalNumber subtract (RationalNumber op2)
{
int commonDenominator = denominator * op2.getDenominator();
int numerator1 = numerator * op2.getDenominator();
int numerator2 = op2.getNumerator() * denominator;
int difference = numerator1 - numerator2;
return new RationalNumber (difference, commonDenominator);
}
//-----------------------------------------------------------------
// Multiplies this rational number by the one passed as a
// parameter.
//-----------------------------------------------------------------
public RationalNumber multiply (RationalNumber op2)
{
int numer = numerator * op2.getNumerator();
int denom = denominator * op2.getDenominator();
return new RationalNumber (numer, denom);
}
//-----------------------------------------------------------------
// Divides this rational number by the one passed as a parameter
// by multiplying by the reciprocal of the second rational.
//-----------------------------------------------------------------
public RationalNumber divide (RationalNumber op2)
{
return multiply (op2.reciprocal());
}
//-----------------------------------------------------------------
// Determines if this rational number is equal to the one passed
// as a parameter. Assumes they are both reduced.
//-----------------------------------------------------------------
public boolean isLike (RationalNumber op2)
{
return ( numerator == op2.getNumerator() &&
denominator == op2.getDenominator() );
}
//-----------------------------------------------------------------
// Returns this rational number as a string.
//-----------------------------------------------------------------
public String toString ()
{
String result;
if (numerator == 0)
result = "0";
else
if (denominator == 1)
result = numerator + "";
else
result = numerator + "/" + denominator;
return result;
}
//-----------------------------------------------------------------
// Reduces this rational number by dividing both the numerator
// and the denominator by their greatest common divisor.
//-----------------------------------------------------------------
private void reduce ()
{
if (numerator != 0)
{
int common = gcd (Math.abs(numerator), denominator);
numerator = numerator / common;
denominator = denominator / common;
}
}
//-----------------------------------------------------------------
// Computes and returns the greatest common divisor of the two
// positive parameters. Uses Euclid's algorithm.
//-----------------------------------------------------------------
private int gcd (int num1, int num2)
{
while (num1 != num2)
if (num1 > num2)
num1 = num1 - num2;
else
num2 = num2 - num1;
return num1;
}
}
每一个对象代表一个有理数。构造方法含有分子和分母两个参数,只需限定分子小于分母,就可以得到一个真分数。
private String getA() {
a = String.valueOf(rnd1.nextInt(10) + 1);
return a;
}
private RationalNumber getB(){
while (true) {
c = rnd1.nextInt(10) + 1;
d = rnd2.nextInt(10) + 1;
b = new RationalNumber(c, d);
if (c < d){
break;
}
}
A是一个随机整数,把它的范围设为1~10,B是一个随机真分数。而每一个操作数既可能为整数,也可能为真分数
public String getOp1(){
if (rnd3.nextInt(2) == 0){
op1 = getA();
}
else
op1 = getB().toString();
return op1;
}
public String getOp2(){
if (rnd3.nextInt(2) == 0){
op2 = getA();
}
else
op2 = getB().toString();
return op2;
}
这样就实现了真分数。
- 支持多运算符
public String getExper(int i){
expr = opd.getOp1() + getOperator();
for (int j = 0; j < i-1; j++) {
String s = opd.getOp1() + getOperator();
expr += s;
}
expr = expr + opd.getOp2();
return expr;
}
用循环的方法来获得多运算符。参数i代表运算符的个数。
- 处理生成题目并输出到文件
package Arithmetic;
import java.io.*;
/**
* Created by Administrator on 2017/5/19.
*/
public class IOFile {
PrintStream ps;
public IOFile(String file){
try {
ps = new PrintStream(file);
} catch (FileNotFoundException e) {
e.printStackTrace();
}
}
public void WriteQuestionsToFile(String s){
ps.append(s);// 在已有的基础上添加字符串
}
}
将题目写入文件,用到了PrinterStream类和它的append方法。只需调用该方法,并将表达式作为一个字符串传入参数即可。
- 完成题目后从文件读入并判题
public static void main(String[] args) throws IOException{
Judgement jdg = new Judgement();
NifixToSuffix nts = new NifixToSuffix();
NumberFormat fmt = NumberFormat.getPercentInstance();
FileInputStream fis = new FileInputStream("Exercises.txt");
InputStreamReader isr = new InputStreamReader(fis);
BufferedReader in = new BufferedReader(isr);
StringTokenizer tokenizer1 = null, tokenizer2 = null;
String token1, token2, token3, token4;
String s1 = null;
String str;
int q = 0, count = 0;
IOFile iof = new IOFile("ExercisesResult.txt");
while ((str = in.readLine()) != null) {
tokenizer1 = new StringTokenizer(str, ":");
token1 = tokenizer1.nextToken();
token2 = tokenizer1.nextToken();
tokenizer2 = new StringTokenizer(token2, "=");
token3 = tokenizer2.nextToken();
token4 = tokenizer2.nextToken();
nts.conversion(token3);
if (token4.equals(jdg.evaluate(nts.getMessage()))) {
s1 = "正确!";
q++;
} else {
s1 = "错误,正确答案为:" + jdg.evaluate(nts.getMessage());
}
String s2 = str + "\n" + s1 + "\n\n";
iof.WriteQuestionsToFile(s2);
count++;
}
double accuracy = (double) q / count;
String s3 = "完成" + count + "道题目,答对" + q + "道题,正确率为" + fmt.format(accuracy);
iof.WriteQuestionsToFile(s3);
}
文件中每个题目都是一行,且形式都为“题目1:表达式 =答案”。是用BufferedReader中的readLine方法,读取一行之后,先以“:”为标记将字符串分开。把“题目n”赋值给token1,“表达式 =答案”赋值给token2,再将token2以“=”为标记,把表达式赋值给token3,答案赋值给token4。将token3转化为后缀表达式,进行计算,把计算结果与token4进行比较,再把整个结果写入到文件中。这样一直循环,直到文件中没有下一行为止。
- 实现分数的运算
用RationalNumber类。定义好加减乘除四种方法。在栈中进行计算时,每取出一个操作数,先将其转化为RationalNumber类型。具体转化方法如下
public RationalNumber tranIntoRationalNum (String s){
String token1, token2;
StringTokenizer tokenizer1 = new StringTokenizer(s, "/");
token1 = tokenizer1.nextToken();
if (tokenizer1.hasMoreTokens()) {
token2 = tokenizer1.nextToken();
r = new RationalNumber(Integer.parseInt(token1), Integer.parseInt(token2));
}
else {
r = new RationalNumber(Integer.parseInt(token1),1);
}
return r;
}
把每个操作数(String类型)以“/”为标记分开,第一个字符传入分子,第二个传入分母;如只有一个,则第一个传入分子,把“1”传入分母。从栈中取出操作数时,调用这个方法,就能将操作数转化为RationalNumber类型。再调用其中的加减乘除的方法进行计算。
private String evalSingleOp (char operation, RationalNumber op1, RationalNumber op2)
{
RationalNumber result = new RationalNumber(0,1);
switch (operation)
{
case ADD:
result = r1.add(r2);
break;
case SUBTRACT:
result = r1.subtract(r2);
break;
case MULTIPLY:
result = r1.multiply(r2);
break;
case DIVIDE:
result = r1.divide(r2);
}
return result.toString();
}
最终返回结果,为String类型。
四、测试方法
- CalculatorTest
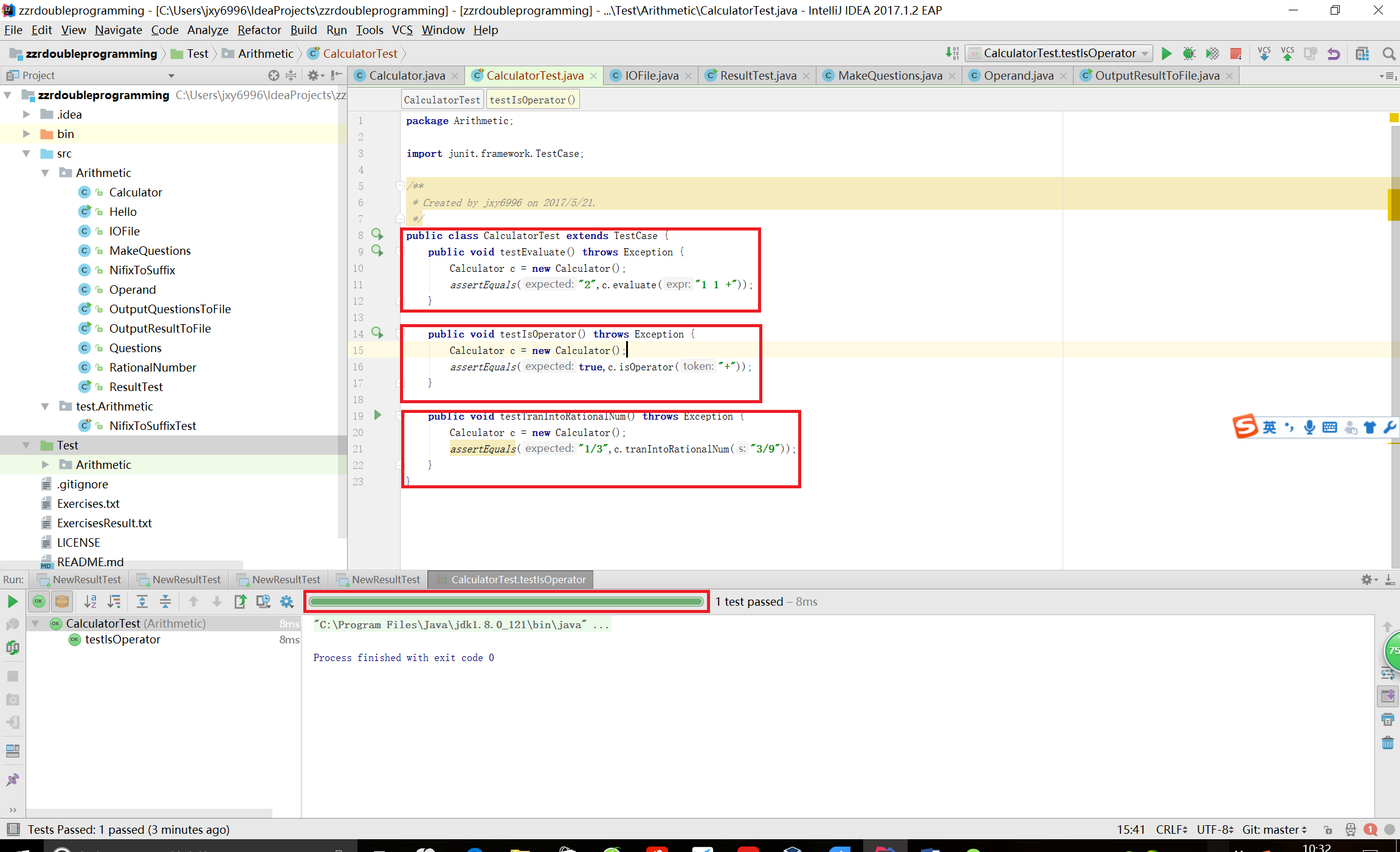
- NifixToSuffixTest
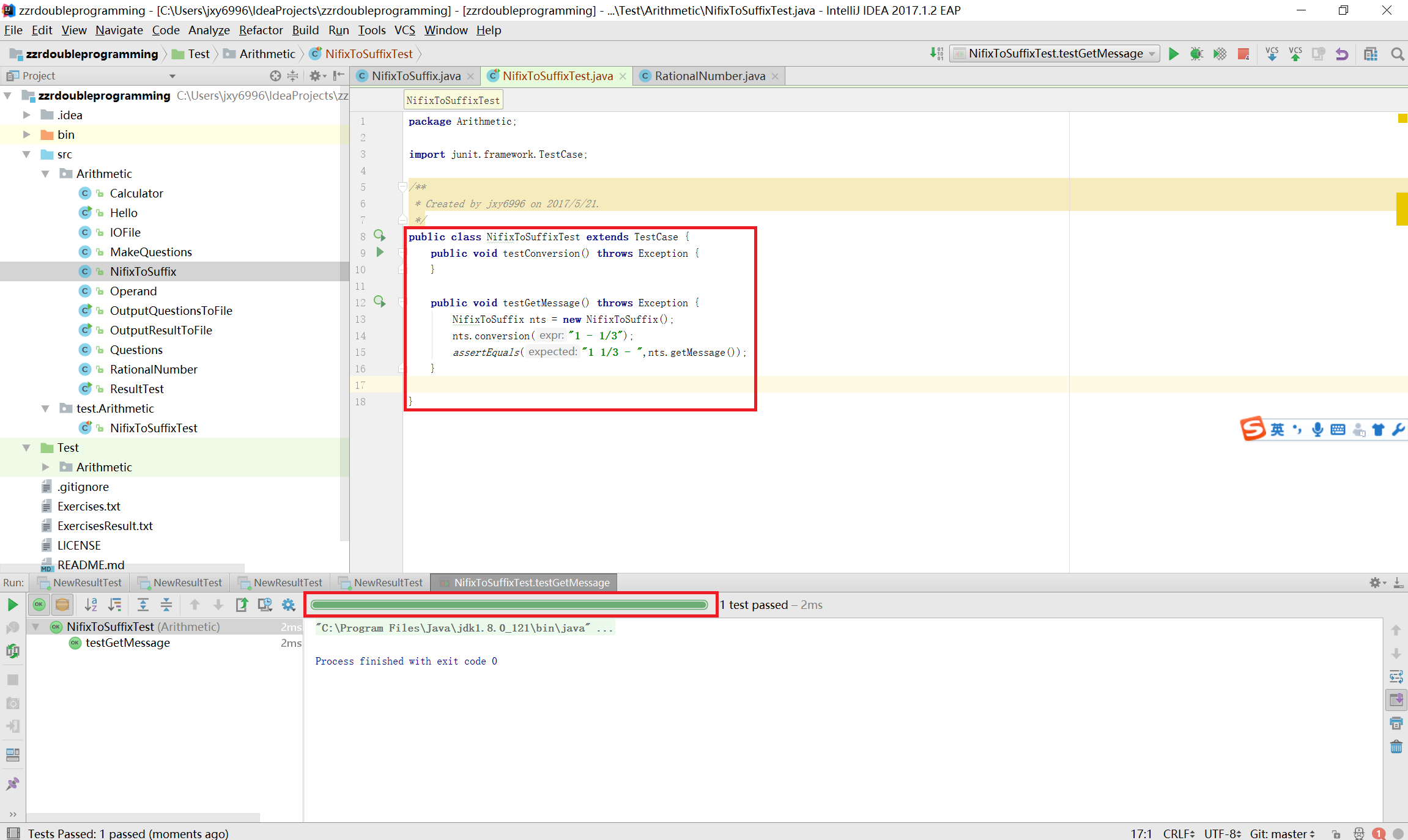
- RationalNumberTest

五、运行过程截图
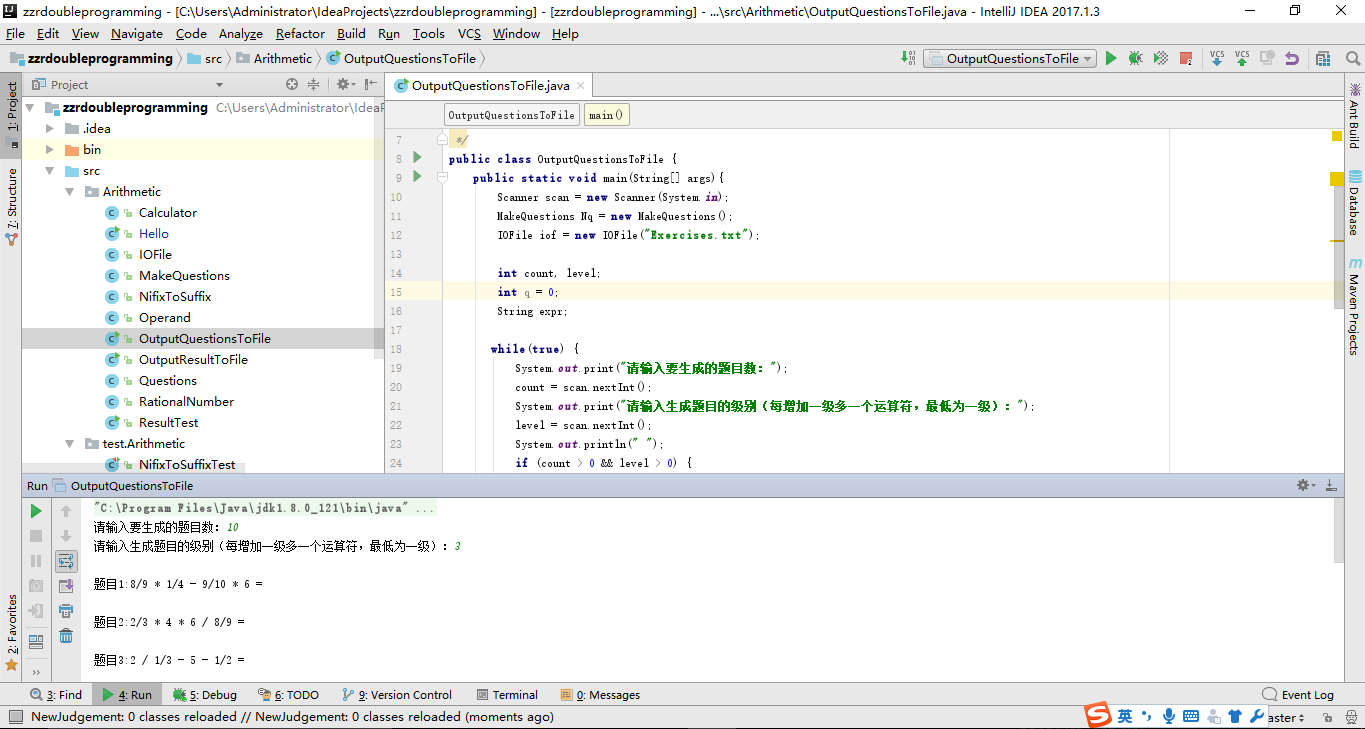
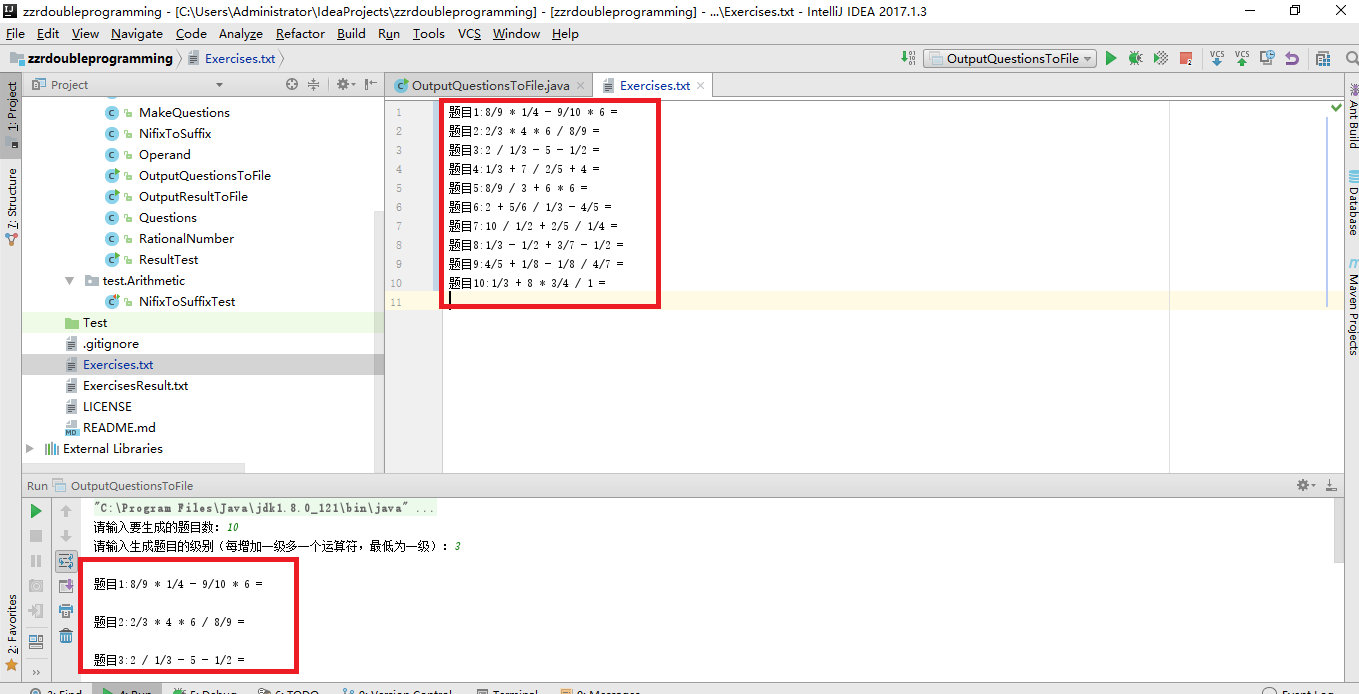
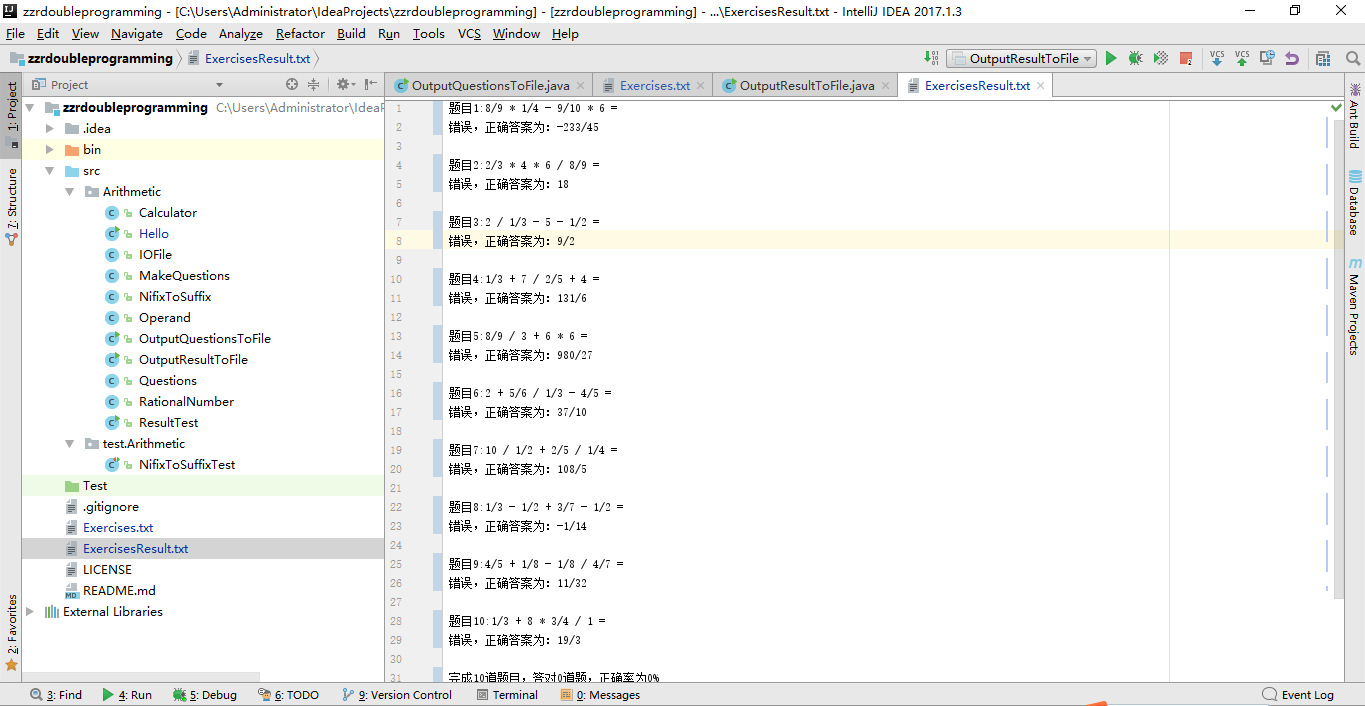
六、代码托管地址
七、遇到的困难及解决方法
- 问题1
生成表达式的时候出现了null字符
- 解决办法
源代码如下
public String getExper(int i){
//用循环的方法来获取多运算符
for (int j = 0; j < i; j++) {
String s = opd.getOp1() + getOperator();
expr += s;
}
expr = expr + opd.getOp2();
return expr;
}
因为expr初始值为空,如果直接执行expr += s语句,会多出一个null字符
修改代码如下
public String getExper(int i){
//用循环的方法来获取多运算符
expr = opd.getOp1() + getOperator();
for (int j = 0; j < i-1; j++) {
String s = opd.getOp1() + getOperator();
expr += s;
}
expr = expr + opd.getOp2();
return expr;
}
先给expr赋值,再进行循环,循环的次数比之前少一次,就可以了
八、对结对的小伙伴的评价
-
结对搭档:20162311张之睿博客
-
评价
这周张之睿给出设计思路并指导我写了一些简单的代码,自主完成了注释和修改类名。发现知识欠缺得挺多,很多地方还需要他进一步解释才能理解。但我一定会多加巩固,努力能逐步实现独立编程。
九、参考或引用的设计、实现
RationalNumber类
这是教材上定义好的类,使用它生成真分数,并进行计算,得到的结果也可以用分数形式展现。
十、PSP
| PSP2.1 | Personal Software Process Stages | 预估耗时(小时) | 实际耗时(小时) |
|---|---|---|---|
| Planning | 计划 | ||
| · Estimate | · 估计这个任务需要多少时间 | 0.5 | 0.5 |
| Development | 开发 | ||
| · Analysis | · 需求分析 (包括学习新技术) | 2 | 4 |
| · Design Spec | · 生成设计文档 | 1.5 | 1 |
| · Design Review | · 设计复审 (和同事审核设计文档) | 1 | 1 |
| · Coding Standard | · 代码规范 (为目前的开发制定合适的规范) | 0.5 | 1 |
| · Design | · 具体设计 | 2 | 3 |
| · Coding | · 具体编码 | 6 | 8 |
| · Code Review | · 代码复审 | 2 | 2.5 |
| · Test | · 测试(自我测试,修改代码,提交修改) | 2 | 2.5 |
| Reporting | 报告 | ||
| · Test Report | · 测试报告 | 1 | 1.5 |
| · Size Measurement | · 计算工作量 | 0.5 | 0.5 |
| · Postmortem & Process Improvement Plan | · 事后总结, 并提出过程改进计划 | 0.5 | 0.5 |
| 合计 | 19.5 | 26 |




