【数据结构】线段树 （一） 学习笔记

线段树（一）

线段树是一种维护区间信息常用的树形数据结构。在全国青少年信息学奥林匹克竞赛大纲内难度评级为 6，是提高级中开始学习的数据结构。

本篇文章讨论的内容是线段树的基本结构与操作、线段树的延迟更新。

基本结构

线段树是用来维护区间信息的树形结构，每个节点表示一个区间的信息。
通常使用存储完全二叉树的数组存储法来存线段树，具体地，节点 \(p\) 的左右子树分别是 \(p*2\) 和 \(p*2+1\) 节点。
理论上，线段树最多只有 \(2*N-1\) 个节点，但是在某些情况下，下标会超过 \(2*N\) (例如 \(N=6\) 时的线段树节点下标最大到了 \(13\))，所以线段树一般开 \(4\) 倍空间。
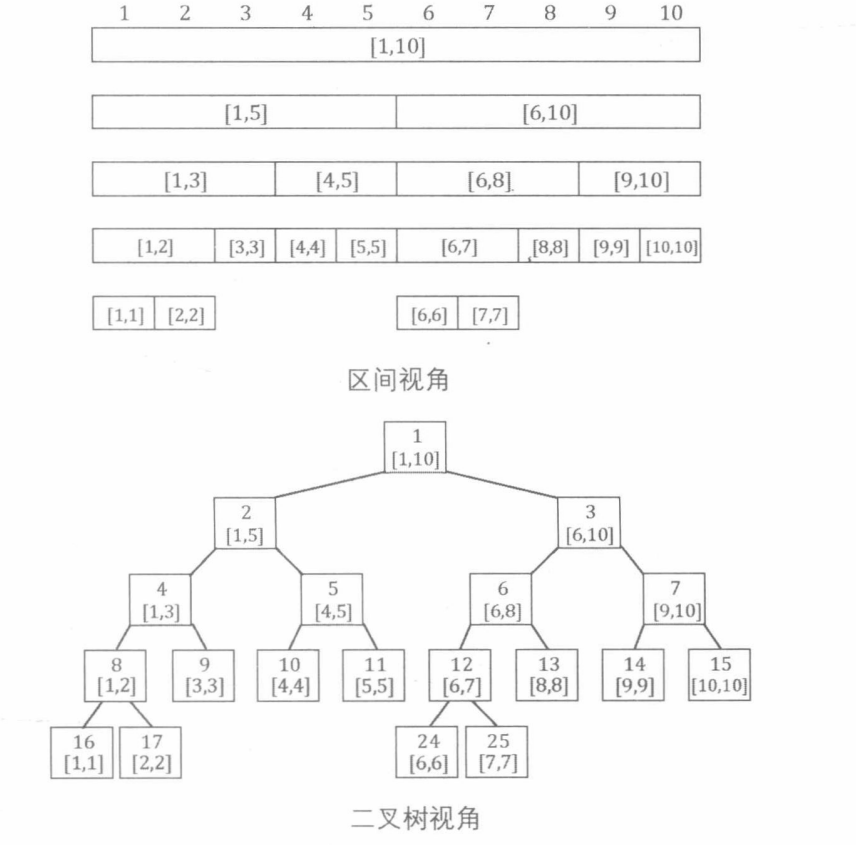
每个节点存储一个区间的信息，其中，根节点存储整个序列 \([1,N]\) 的信息，设节点 \(p\) 存储区间 \([L,R]\) 的信息，则节点 \(p*2\) 和 \(p*2+1\) 分别存储区间 \([L,mid]\) 和 \([mid+1,R]\) 的信息，其中 \(mid=\lfloor \frac{L+R}{2} \rfloor\)。区间大小为 \(1\) 的节点是线段树的叶子节点。
下图说明了线段树的结构，图来自《算法竞赛进阶指南》：

基本操作：建立，单点修改与查询

线段树的建树操作递归实现，对于一个节点的建立，先建立他的左右子树，再根据他的左右子树信息合并得到他的信息（从下往上传递信息）。
线段树的单点修改，要先递归找到修改的叶子节点，然后将修改后的信息向上传递。单点查询即找到这个点代表的叶子节点，代码实现与单点修改类似。
线段树的区间查询，通过判断查询的区间是否和左右子树表示的区间有交集，合并有交集的区间内的信息。

时间复杂度分析：建树操作为 \(n \log n\)，每次单点修改或查询需要经过树上的一条链，时间复杂度为 \(O(\log n)\)。每次区间查询操作会把询问在树上的 \(\log n\) 个节点。

参考代码（维护的信息是区间最大值）：

洛谷 P1198 [JSOI2008] 最大数

// https://www.luogu.com.cn/problem/P1198
#include <iostream>
using namespace std;
 
#define lc(p) ((p)<<1)
#define rc(p) ((p)<<1|1)
#define int long long
const int N = 2e5 + 5;
int n;
struct node {
    int l, r;
    int val;
} t[4 * N];
 
void push_up(int p) {
    t[p].val = max(t[lc(p)].val, t[rc(p)].val); // 向上传递信息
}
 
void build(int p, int l, int r) {
    t[p].l = l, t[p].r = r;
    if (l == r) return; // 叶子节点，初始值是 0 
    int mid = (l + r) >> 1;
    build(lc(p), l, mid);
    build(rc(p), mid + 1, r);
    push_up(p); // 向上传递信息，完成建树
}
 
void change(int p, int id, int x) { // 单点修改
    if (t[p].l == t[p].r) {
        t[p].val = x;
        return;
    }
    int l = t[p].l, r = t[p].r;
    int mid = (l + r) >> 1;
    if (id <= mid) change(lc(p), id, x); // 递归寻找叶子节点
    else change(rc(p), id, x);
    push_up(p); // 自下而上更新信息
}
 
int query(int p, int l, int r) { // 区间查询
    if (t[p].l >= l && t[p].r <= r) // 若节点完全包含在查询区间内可以直接返回
        return t[p].val;
    int ans = 0, mid = (t[p].l + t[p].r) >> 1;
    if (l <= mid) ans = query(lc(p), l, r); // 左右区间有交集的合并信息
    if (r > mid) ans = max(ans, query(rc(p), l, r));
    return ans;
}
 
signed main() {
    ios::sync_with_stdio(0);
    #ifndef ONLINE_JUDGE
    freopen("data.in", "r", stdin);freopen("data.out", "w", stdout);
    #endif
    int m, d;
    cin >> m >> d;
    build(1, 1, m);
    int t=0;
    for (int i = 1;i <= m;i++) {
        char op;
        cin >> op;
        if (op == 'Q') {
            int l;
            cin >> l;
            cout << (t = query(1, n - l + 1, n)) << endl;
        }
        else {
            int x;
            cin >> x;
            change(1, n + 1, (x + t) % d);
            n++;
        }
    }
    return 0;
}

延迟更新：区间修改

线段树最强大的功能是可以 \(O(\log n)\) 实现的区间修改，显然不是对区间内每个点进行单点修改。
具体的，如果要修改一个区间，那就按照类似区间查询的实现方式，从根节点开始递归。如果当前节点不完全包含修改区间就向左右子树递归，否则就在这个节点上记录一个延迟更新（lazy tag）数据，返回即可。
lazy tag 是含义是：该节点被修改，但是修改数据没有下传到其子节点。再次修改或查询某节点时，将这个节点上的 lazy tag 下传到其子节点。时间复杂度与区间查询相同。

代码实现如下：

洛谷 P3372 【模板】线段树 1

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define lc(x) ((x)<<1)
#define rc(x) (((x)<<1)|1)
 
const int N = 1e5 + 5;
 
struct node {
    int l, r;
    int v, add;
} t[4 * N];
 
int a[N], n;
 
void push_up(int p) {
    t[p].v = t[lc(p)].v + t[rc(p)].v;
}
 
void push_down(int p) {
    if (t[p].add) {
        t[lc(p)].add += t[p].add, t[lc(p)].v += t[p].add * (t[lc(p)].r - t[lc(p)].l + 1);
        t[rc(p)].add += t[p].add, t[rc(p)].v += t[p].add * (t[rc(p)].r - t[rc(p)].l + 1);
        t[p].add = 0;
    }
}
 
void build(int p, int l, int r) {
    t[p].l = l, t[p].r = r;
    if (l == r) {
        t[p].v = a[l];
        return;
    }
    int mid = (l + r) / 2;
    build(lc(p), l, mid);
    build(rc(p), mid + 1, r);
    push_up(p);
}
 
int query(int p, int l, int r) {
    if (l <= t[p].l && t[p].r <= r)
        return t[p].v;
    push_down(p);
    int mid = (t[p].l + t[p].r) / 2, ans = 0;
    if (l <= mid) ans += query(lc(p), l, r);
    if (mid < r) ans += query(rc(p), l, r);
    return ans;
}
 
void change(int p, int l, int r, int k) {
    if (l <= t[p].l && t[p].r <= r) {
        t[p].add += k;
        t[p].v += (t[p].r - t[p].l + 1) * k;
        return;
    }
    push_down(p);
    int mid = (t[p].l + t[p].r) / 2;
    if (l <= mid) change(lc(p), l, r, k);
    if (mid < r) change(rc(p), l, r, k);
    push_up(p);
}
 
signed main() {
    ios::sync_with_stdio(0);
    #ifndef ONLINE_JUDGE
    freopen("data.in", "r", stdin);freopen("data.out", "w", stdout);
    #endif
    int m;
    cin >> n >> m;
    for (int i = 1;i <= n;i++) cin >> a[i];
    build(1, 1, n);
    for (int i = 1;i <= m;i++) {
        int op, l, r, k;
        cin >> op;
        if (op == 1) {
            cin >> l >> r >> k;
            change(1, l, r, k);
        }
        else {
            cin >> l >> r;
            cout << query(1, l, r) << endl;
        }
    }
    return 0;
}

推荐题目 && 参考资料 && 拓展阅读

• 《算法竞赛进阶指南》 0x43 线段树
• P3870 [TJOI2009] 开关
• P1438 无聊的数列
• P1253 扶苏的问题
• P3373 【模板】线段树 2
• P4513 小白逛公园
• P1471 方差