【计算几何】学习笔记
计算几何
用计算机解决几何问题,显然计算机(至少在 OI/CPC 中)是不能处理复杂的图形的,所以解决方法和数学中解析几何类似。
直线
直线有四种表示方法:斜截式,点斜式,两点式,一般式。
斜截式:\(y=kx+b\),其中 \(k\) 为直线的斜率,\(b\) 为截距。两点(设为\((x_1,y_1),(x_2,y_2)\))确定一条直线,则这条直线的斜率 \(k = \frac{x_1-x_2}{y_1-y_2}\)。注意当直线平行于 \(y\) 轴时不能用斜截式表示。
点斜式:对求斜率公式移项,把一个点当任意点,另一个点坐标已知(设为\((x_0,y_0)\)),则有 \(y - y_0 = k (x - x_0)\)
例题:luogu P1142 轰炸
先枚举直线(枚举两点计算斜率),然后计算有多少点在这条直线上(带入点斜式公式),取最大值即可。
参考代码:
#include <bits/stdc++.h>
using namespace std;
const int N = 705;
const double eps = 1e-8;
int n, ans = 1;
int x[N], y[N];
bool dcmp(double x, double y)
{
return abs(x - y) <= eps;
}
double calc_k(int x_1, int y_1, int x_2, int y_2)
{
return double(y_1 - y_2) / (x_1 - x_2);
}
signed main()
{
ios::sync_with_stdio(false);
#ifdef DEBUG
freopen("data.in", "r", stdin);
freopen("data.out", "w", stdout);
#endif
// Don't stop. Don't hide. Follow the light, and you'll find tomorrow.
cin >> n;
for (int i = 1; i <= n; i++)
cin >> x[i] >> y[i];
for (int i = 1; i <= n; i++)
for (int j = i + 1; j <= n; j++)
if (x[i] != x[j])
{
int res = 0;
double k = calc_k(x[i], y[i], x[j], y[j]);
for (int p = 1; p <= n; p++)
res += dcmp(y[p] - y[i], k * (x[p] - x[i]));
ans = max(ans, res);
}
else // 平行于 y 轴的直线
{
int res = 0;
for (int p = 1; p <= n; p++)
res += x[p] == x[i];
ans = max(ans, res);
}
cout << ans << endl;
return 0;
}
三角形
把三角形\(\triangle ABC\)放到直角坐标系里,记三个顶点为 \((x_A,y_A),(x_B,y_B),(x_C,y_C)\),则有下面几个性质。
面积
著名海伦公式指出:\(S = \sqrt{p(p-a)(p-b)(p-c)}\),其中 \(p = \frac12(a+b+c)\)。在直角坐标系中,根据两点之间距离公式知边长 \(a = \sqrt{(x_B - x_C) ^ 2 + (y_B - y_C) ^ 2}\)
点与三角形的关系
- 点在三角形上:可分为在顶点上和在边上,略。
- 点在三角形内:记点 \(P(x_P,y_P)\),则 \(S_{\triangle ABC} = S_{\triangle ABP} + S_{\triangle ACP} + S_{\triangle BCP}\)。
- 点在三角形外:记点 \(P(x_P,y_P)\),则 \(S_{\triangle ABC} < S_{\triangle ABP} + S_{\triangle ACP} + S_{\triangle BCP}\)。
例题:P1355 神秘大三角 的参考代码:
#include <bits/stdc++.h>
using namespace std;
// #define int long long
using point = pair<double, double>;
const double eps = 1e-6;
point A, B, C, P;
bool dcmp(double x, double y)
{
return abs(x - y) <= eps;
}
double calc_len(const point &p, const point &q)
{
return sqrt(pow(p.first - q.first, 2) + pow(p.second - q.second, 2));
}
double calc_k(const point &p, const point &q)
{
return (p.second - q.second) / (p.first - q.first);
}
double calc_triS(const point &pa, const point &pb, const point &pc) // 海伦公式
{
double a = calc_len(pb, pc), b = calc_len(pa, pc), c = calc_len(pa, pb);
double p = 0.5 * (a + b + c);
return sqrt(p * (p - a) * (p - b) * (p - c));
}
signed main()
{
#ifdef DEBUG
freopen("data.in", "r", stdin);
freopen("data.out", "w", stdout);
#endif
// Don't stop. Don't hide. Follow the light, and you'll find tomorrow.
scanf("(%lf,%lf)\n", &A.first, &A.second);
scanf("(%lf,%lf)\n", &B.first, &B.second);
scanf("(%lf,%lf)\n", &C.first, &C.second);
scanf("(%lf,%lf)\n", &P.first, &P.second);
if (P == A || P == B || P == C)
puts("4");
else if (calc_k(A, P) == calc_k(A, B) || calc_k(B, C) == calc_k(B, P) || calc_k(C, A) == calc_k(C, P))
puts("3");
else if (dcmp(calc_triS(A, B, C), calc_triS(A, B, P) + calc_triS(A, C, P) + calc_triS(B, C, P)))
puts("1");
else
puts("2");
return 0;
}
原圆
圆的标准方程:\((x-x_P)^2+(y-y_P)^2 = r^2\),其中圆心是 \(P(x_P,y_P)\),半径是 \(r\)。
点和圆,直线与圆的位置关系初中已经学过,这里不多赘述。
二维凸包
凸集:平面的一个子集,并且形状是“凸”的。“凸”准确地说就是在集合内部取任意两点,它们连成的线段仍完全处于内部,如下图。
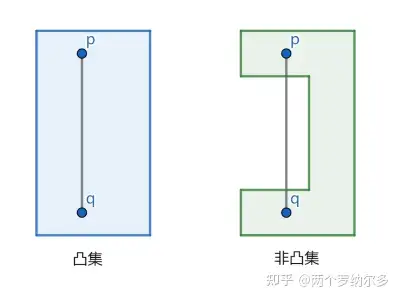
凸包:给定 \(n\) 个点,找出包含所有点的周长最小的凸集就是凸包,如下图所示。