【图论】基环树 学习笔记
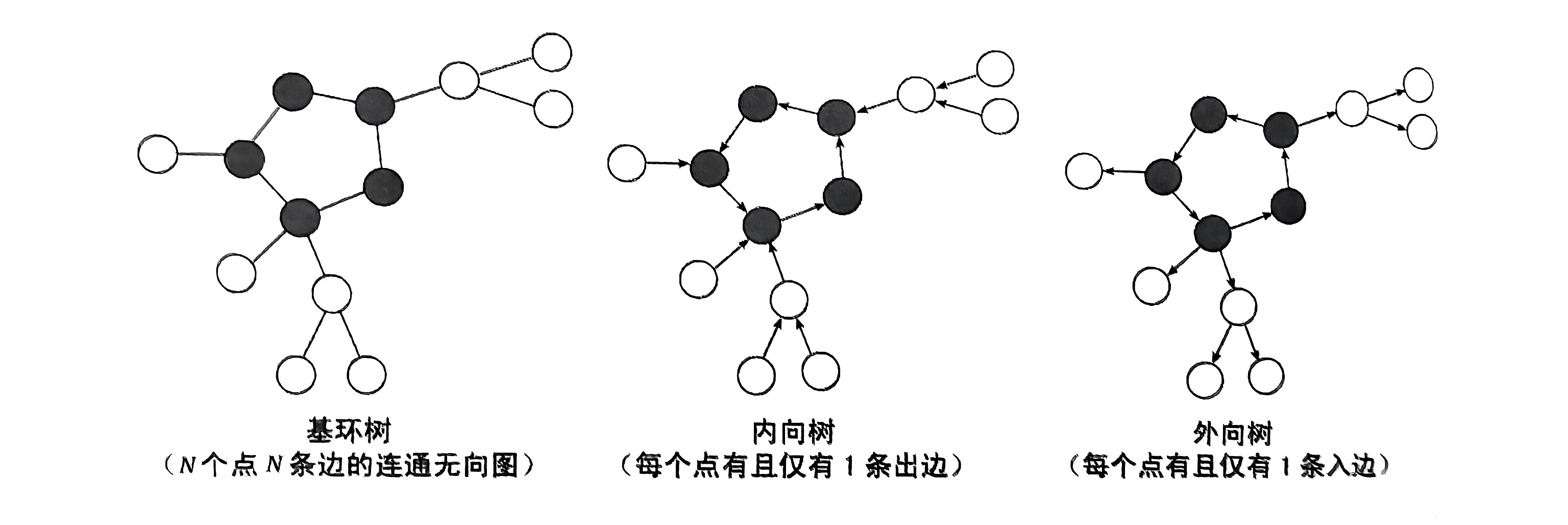
基环树
下面几个条件互相等价:
- 一个连通的图是基环树
- 联通块有 n 个点 n 条边
- 图上存在且仅存在一个环,且环上每个节点是一颗子树的根。
通常情况下树指的都是无向图,但是有向图也可以构成基环树。
内向基环树:每个点都有一条出边。容易发现沿着这条边一定会走到环上“向内走”。
外向基环树:每个点都有一条入边。容易发现沿着这条边一定会走出环,形象理解为“向外走”。
当 n 个点 n 条边的图不联通时,图是一个基环树森林,即图上每个连通块都是一棵基环树。
可以看一下下面这个图加深印象,图来自《算法竞赛进阶指南》。
基环树的直径
树上任意两节点之间最长的简单路径即为树的「直径」。类似的,我们可以定义基环树的直径。基环树中最长的一条链(简单路径)就是基环树的直径。
下面介绍基环树直径的求法,显然基环树直径有下面两种情况:
- 在去掉环的某条子树上。
- 经过环,端点在两颗不同子树上。
首先拓扑排序找出基环树的环,把划分出来的每颗子树的直径先求出来。
求出直径的同时计算出:\(d[u]\) 表示在点 \(u\) 所在子树以 \(u\) 为端点的最长链。
接下来考虑第二种情况:则相当于求出环上一对点,使得 \(d[x] + d[y] + dis(x,y)\) 最大。
单独把这个问题抽象出来:
环上每个点有点权(记作 \(d[i] > 0\) ),两点之间有边权(记作 \(dis(x,y) > 0\)),两点间距离为点权和加顺时针/逆时针边权中较大的,求最大距离。


