【数据结构】树状数组 学习笔记
树状数组
基本思想
树状数组是一种基于二进制拆分的思想，用来动态维护序列的前缀和的树形数据结构。在全国青少年信息学奥林匹克竞赛大纲内难度评级为 6，是提高级中开始学习的数据结构。
树状数组的基本操作：
- 修改序列中的一个数。
- 查询序列前缀和。
\(lowbit(x)\) 表示将 x 写成二进制表示后，最低位的 1 所代表的数值，如 \(10 = (1010)_2 , lowbit(10)=(10)_2=2\)
以下是 \(lowbit(x)\) 的求法，具体证明可参见 《算法竞赛进阶指南》 0x01 二进制 章节。
#define lowbit(x) ((x)&(-(x)))
对于原序列 \(a[n]\)，树状数组用一个数组 \(c[n]\)，其中，\(c[i]\) 表示以 \(i\) 结尾长度为 \(lowbit(i)\) 的区间和，即区间 \([i-lowbit(i)+1,i]\)。
这时如果把整个数组视作一个树型结构（如下图，图来自《算法竞赛进阶指南》），则有以下性质：
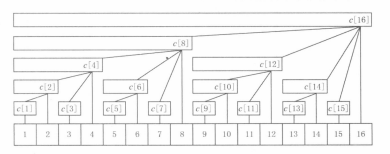
- 每个节点表示以这个节点为根的子树中所有节点的和。
- 每个节点有 \(lowbit(i)\) 个子节点，其中 \(i\) 表示这个节点的编号。
- 每个节点的父节点是 \(i+lowbit(i)\)，其中 \(i\) 表示这个节点的编号。
可以发现，树的深度是 \(O(\log n)\)，所以树状数组的两种基本操作的时间复杂度都是 \(O(\log n)\)。
代码实现
洛谷 P3374 【模板】树状数组 1
a[n] 表示原序列,c[n] 表示树状数组,其中 n 是序列长度。
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 5e5 + 5;
int c[N], n;
#define lowbit(x) ((x)&(-(x)))
inline void add(int id, int x) {
for (int i = id;i <= n;i += lowbit(i)) c[i] += x;
}
inline int query(int id) {
int ans = 0;
for (int i = id;i > 0;i -= lowbit(i)) ans += c[i];
return ans;
}
inline int query(int l, int r) {
// 前缀和思想求区间和
return query(r) - query(l - 1);
}
signed main() {
int m;
ios::sync_with_stdio(false);
cin >> n >> m;
for (int i = 1;i <= n;i++) {
int a;cin >> a;
add(i, a);
}
for (int i = 1;i <= m;i++) {
int op, x, y;
cin >> op >> x >> y;
if (op == 1) add(x, y);
else cout << query(x, y) << endl;
}
return 0;
}
树状数组与逆序对
如果把树状数组当作一个桶使用，则可以用树状数组进行求逆序对等操作。
具体地，因为树状数组可以查询前缀和，所以可以查询比某个数小的数量，据此可统计逆序对数目。
洛谷 P1908 逆序对
注意：此题值域较大，需要对数据进行离散化。
参考代码：
// https://www.luogu.com.cn/problem/P1908
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 5e5 + 5;
int n,
a[N], // 原序列
b[N], m, // 离散化用序列
c[N]; // 树状数组(当桶使用)
long long ans;
#define lowbit(x) ((x)&(-(x)))
void add(int id, int x) {
for (int i = id; i <= n; i += lowbit(i))
c[i] += x;
}
int sum(int id) {
int ans = 0;
for (int i = id;i;i -= lowbit(i)) ans += c[i];
return ans;
}
int query(int x) {
return lower_bound(b + 1, b + 1 + n, x) - b;
}
signed main() {
ios::sync_with_stdio(0);
#ifndef ONLINE_JUDGE
freopen("data.in", "r", stdin);freopen("data.out", "w", stdout);
#endif
cin >> n;
for (int i = 1;i <= n;i++) {
cin >> a[i];
b[i] = a[i];
}
sort(b + 1, b + 1 + n);
m = unique(b + 1, b + 1 + n) - b - 1;
for (int i = 1;i <= n;i++) a[i] = query(a[i]);
for (int i = n;i;i--) {
ans += sum(a[i] - 1);
add(a[i], 1);
}
cout << ans << endl;
}
如果再对当桶使用的树状数组进行拓展，即权值树状数组，可实现一些平衡树的操作，见拓展阅读。
这里再对权值树状数组举一个例题：
洛谷 P1637 三元上升子序列
考虑对于每个数，统计在其前面并小于其的数的个数与在其后面并大于其的个数，统计过程类似于逆序对，可以用权值树状数组，然后枚举 \(j\) 用乘法原理计算即可。
参考代码：
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5;
#define int long long
int n;
int a[N];
struct bit
{
int tr[N], n;
void init(int _n)
{
memset(tr, 0, sizeof tr);
n = _n;
}
void add(int id, int x = 1)
{
for (int i = id; i <= n; i += (i & (-i)))
tr[i] += x;
}
int query(int id)
{
int ret = 0;
for (int i = id; i; i -= (i & (-i)))
ret += tr[i];
return ret;
}
} trl, trr;
int l[N], r[N];
signed main()
{
ios::sync_with_stdio(0);
#ifdef DEBUG
freopen("data.in", "r", stdin);
freopen("data.out", "w", stdout);
#endif
while (cin >> n)
{
trl.init(1e5), trr.init(1e5);
for (int i = 1; i <= n; i++)
cin >> a[i];
for (int i = 1; i <= n; i++)
{
trl.add(a[i]);
l[i] = trl.query(a[i] - 1);
}
for (int i = n; i > 0; i--)
{
trr.add(a[i]);
r[i] = n - i - trr.query(a[i]) + 1;
}
int ans = 0;
for (int i = 1; i <= n; i++)
ans += l[i] * r[i];
cout << ans << endl;
}
}
树状数组与差分
朴素的前缀和区间查询和单点修改的时间复杂度分别是 \(O(1)\)， \(O(n)\)。
树状数组可以将其优化为 \(O(\log n)\)，\(O(\log n)\)。
朴素的差分单点查询和区间修改的时间复杂度分别是 \(O(n)\)， \(O(1)\)。
树状数组同样可以将其优化为 \(O(\log n)\)，\(O(\log n)\)。
代码实现如下：
洛谷 P3368 【模板】树状数组 2
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 5e5 + 5;
int a[N], c[N], n;
inline int lowbit(int x) { return x & (-x); }
inline void add(int id, int x) {
for (int i = id;i <= n;i += lowbit(i)) c[i] += x;
}
void add(int l, int r, int x) {
add(l, x), add(r + 1, -x);
}
inline int query(int id) {
int ans = 0;
for (int i = id;i > 0;i -= lowbit(i)) ans += c[i];
return ans;
}
signed main() {
int m;
ios::sync_with_stdio(false);
cin >> n >> m;
for (int i = 1;i <= n;i++) cin >> a[i];
for (int i = 1;i <= n;i++) {
if (i == 1) add(1, a[1]);
else add(i, a[i] - a[i - 1]); // 差分
}
for (int i = 1;i <= m;i++) {
int op, x;
cin >> op;
if (op == 1) {
int y, k;
cin >> x >> y >> k;
add(x, y, k);
}
else cin >> x, cout << query(x) << endl;
}
return 0;
}
考虑区间查询，有：\(\sum_{i=1}^x a[i]\)
而差分（\(b[i]\)是差分数组）有： \(a[i]=\sum_{j=1}^i b[i]\)
考虑每一个 \(b[i]\) 被求和的次数（如图，图来自《算法竞赛进阶指南》），化简一下式子：
\[\sum_{i=1}^x \sum_{j=1}^i b[i] = \sum_{i=1}^x (x-i+1) * b[i] = \sum_{i=1}^x (x+1) *b[i] - i*b[i] = \newline (x+1) \sum_{i=1}^x b[i] - \sum_{i=1}^x i*b[i]
\]
用树状数组分别维护 \(b[i]\) 和 \(i*b[i]\) 即可维护上面式子，区间查询和区间修改的时间复杂度都是 \(O(\log n)\)。
代码实现如下：
LibreOJ #132. 树状数组 3 ：区间修改，区间查询
// https://loj.ac/p/132
#include <iostream>
using namespace std;
#define lowbit(x) ((x)&(-(x)))
#define int long long
const int N = 1e6 + 5;
int a[N]; // 原数组
int b[N]; // 差分数组
int c[3][N], n; // 树状数组,c[1]维护b[i],c[2]维护i*b[i]
void add(int k, int id, int x) {
for (int i = id;i <= n;i += lowbit(i)) c[k][i] += x;
}
void add(int k, int l, int r, int x) {
if (k == 1) add(k, l, x), add(k, r + 1, -x);
else add(k, l, l * x), add(k, r + 1, -(r + 1) * x);
}
int query(int k, int id) {
int ans = 0;
if (k > 0) {
for (int i = id;i;i -= lowbit(i)) ans += c[k][i];
return ans;
}
return (id + 1) * query(1, id) - query(2, id);
}
int query(int k, int l, int r) {
return query(k, r) - query(k, l - 1);
}
signed main() {
ios::sync_with_stdio(0);
#ifndef ONLINE_JUDGE
freopen("data.in", "r", stdin);
freopen("data.out", "w", stdout);
#endif
int q;
cin >> n >> q;
for (int i = 1;i <= n;i++) {
cin >> a[i];
b[i] = a[i] - a[i - 1];
}
for (int i = 1;i <= n;i++) {
add(1, i, b[i]);
add(2, i, i * b[i]);
}
while (q--) {
int op;
cin >> op;
if (op == 1) {
int l, r, x;
cin >> l >> r >> x;
add(1, l, r, x);
add(2, l, r, x);
}
else {
int l, r;
cin >> l >> r;
cout << query(0, l, r) << endl;
}
}
return 0;
}
参考资料 && 拓展阅读 && 推荐题目
- 《算法竞赛进阶指南》，李煜东著，0x42 树状数组
- AcWing 算法提高课 4.2 树状数组
- 洛谷日报 #416 [5k_sync_closer] 浅谈权值树状数组及其扩展
- AcWing 241. 楼兰图腾 提示：树状数组求逆序对+组合计数
- AcWing 244. 谜一样的牛 提示：树状数组+二分/倍增
- AcWing 260. 买票
- 洛谷题单 CMの树状数组
