【数据结构】并查集 学习笔记
并查集
基础知识
并查集是一种树形数据结构。在全国青少年信息学奥林匹克系列竞赛大纲中难度为 6,是提高级中学习的数据结构。
并查集的基本操作:
- 查询一个元素在哪个集合。
- 合并两个集合。
使用一个森林来存储并查集,一个元素是一个结点,每棵树是一个集合。用一个数组 f 来记录父亲表示法。即 f[x] 表示元素节点 x 的父亲。这样,查询一个元素在哪个集合就是查询节点所在树的根节点,合并两个集合,就是把一颗树的根节点的父亲设置成另外一棵树的根节点。
并查集的优化
并查集有两种常用的优化操作,一种优化查询,一种优化合并。
查询:使用路径压缩,比较常用。容易发现,并查集只需要元素所在树的根节点,树的形态对操作没有影响。所以,可以在查询的时候,把所有查询的节点的父亲直接改成树根。(图来自《算法竞赛进阶指南》)
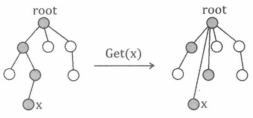
合并:使用启发式合并。把节点少的树合并到节点多的树上,通常在带权并查集中使用。这里不过多介绍,请参考拓展阅读相关资料。
并查集的代码实现
洛谷 P3367 【模板】并查集
题目链接
并查集模板,要注意初始化,即每个元素所在的集合最开始只有自身。
#include <iostream>
using namespace std;
// 1. 并查集的存储
int f[100005], n; // 并查集中有 n 个元素
// 2. 并查集的查询(带路径压缩优化)
int get(int x)
{
if (f[x] == x)
return x; // x 是根节点
return f[x] = get(f[x]); // 递归寻找根节点,并且进行路径压缩
}
// 3. 并查集的合并
void merge(int x, int y)
{
f[get(x)] = get(y);
}
int main()
{
int m;
cin >> n >> m;
for (int i = 1; i <= n; i++)
f[i] = i; // 4. 并查集的初始化
while (m--) {
int x, y, z;
cin >> z >> x >> y;
if (z == 1)
merge(x, y);
else {
if (get(x) == get(y))
cout << 'Y' << endl;
else
cout << 'N' << endl;
}
}
return 0;
}
维护传递关系
并查集可以维护具有传递性的关系。也就是说,如果题目中出现的关系有如下性质:若 A 与 B 有这种关系,且 B 与 C 有这种关系,则 A 与 C 也有这种关系。如无向图中节点的连通性等。
洛谷 P1955 [NOI2015] 程序自动分析
题意:
考虑一个约束满足问题的简化版本:假设 x1,x2,x3,… 代表程序中出现的变量,给定 n 个形如 xi=xj 或 xi≠xj 的变量相等/不等的约束条件,请判定是否可以分别为每一个变量赋予恰当的值,使得上述所有约束条件同时被满足。
例如,一个问题中的约束条件为:x1=x2,x2=x3,x3=x4,x1≠x4,这些约束条件显然是不可能同时被满足的,因此这个问题应判定为不可被满足。
现在给出一些约束满足问题,请分别对它们进行判定。
思路:
变量之间的相等关系具有传递性。先把所有相等的变量用并查集合并,然后判断每个不等关系的条件,如果有两个变量不相等但是在同一集合内,则判断为不能满足,否则可以满足。所有条件可以被满足则约束关系可以被满足。另外,这题数据范围中的 i, j 较大,需要离散化处理数据。
参考代码:
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1000005;
int t, fa[2 * N], n, i1[N], i0[N], a1, j1[N], j0[N], a0;
int a[N], b[N], m;
int get(int x)
{
return (fa[x] == x) ? x : (fa[x] = get(fa[x]));
}
int query(int x) // 离散化
{
return lower_bound(b, b + m, x) - b;
}
int main()
{
ios::sync_with_stdio(0);
cin >> t; // 多组测试数据
while (t--)
{
cin >> n;
m = a1 = a0 = 0;
for (int i = 1; i <= 2 * n; i++)
fa[i] = i;
for (int i = 1; i <= n; i++)
{
int x, y, z;
cin >> x >> y >> z;
if (z == 0) // 变量相等
{
a0++;
i0[a0] = x, j0[a0] = y;
}
if (z == 1) // 变量不等
{
a1++;
i1[a1] = x, j1[a1] = y;
}
a[2 * i - 1] = x, a[2 * i] = y;
}
sort(a + 1, a + 1 + 2 * n);
for (int i = 1; i <= 2 * n; i++)
{
if (i == 1 || a[i] != a[i - 1])
b[++m] = a[i];
}
for (int i = 1; i <= a1; i++)
{
fa[get(query(i1[i]))] = get(query(j1[i]));
}
bool flag = 1;
for (int i = 1; i <= a0 && flag; i++)
{
flag &= (get(query(i0[i])) != get(query(j0[i])));
}
cout << ((flag) ? ("YES") : ("NO")) << endl;
}
return 0;
}
统计并查集集合个数
在一些题中,需要我们统计并查集中集合个数。统计有多少树的根节点即可(根节点的父节点是他本身)
我们来看下面这题:
洛谷 P1536 村村通
题目描述:
某市调查城镇交通状况,得到现有城镇道路统计表。表中列出了每条道路直接连通的城镇。市政府 "村村通工程" 的目标是使全市任何两个城镇间都可以实现交通(但不一定有直接的道路相连,只要相互之间可达即可)。请你计算出最少还需要建设多少条道路?
输入格式:
输入包含若干组测试数据,每组测试数据的第一行给出两个用空格隔开的正整数,分别是城镇数目 n 和道路数目 m;随后的 m 行对应 m 条道路,每行给出一对用空格隔开的正整数,分别是该条道路直接相连的两个城镇的编号。简单起见,城镇从 1 到 n 编号。注意:两个城市间可以有多条道路相通。在输入数据的最后,为一行一个整数 0,代表测试数据的结尾。
输出格式:
对于每组数据,对应一行一个整数。表示最少还需要建设的道路数目。
做法:
初始时,我们用并查集把所有直接连通的城镇合并。统计出集合数,显然集合数减一就是最少要建设的道路。
参考代码:
#include <iostream>
using namespace std;
int f[1005], n, m;
int get(int x)
{
// 1. 并查集的查询,这里我用三元表达式压了下行
return (f[x] == x) ? (x) : (f[x] = get(f[x]));
}
int main()
{
ios::sync_with_stdio(0);
do {
cin >> n;
if (n == 0)
break;
cin >> m;
for (int i = 1; i <= n; i++)
f[i] = i;
for (int i = 1; i <= m; i++) {
int x, y;
cin >> x >> y;
f[get(x)] = get(y); // 2. 并查集的合并
}
int ans = 0;
for (int i = 1; i <= n; i++)
ans += (i == get(i)); // 3. 统计集合个数(就是统计根节点个数)
cout << ans - 1 << endl;
} while (n != 0);
return 0;
}
带权并查集
有时候,我们除了需要并查集的两个基本操作外,还需要维护节点或者集合的一些其他信息。当我们维护集合的信息时,可以把信息记在集合的根节点上。当我们维护节点的信息是节点到根节点的距离或者其他与根节点相关的信息时,就使用边带权并查集,把信息记在节点到父节点的边上,在路径压缩时处理。
洛谷 P1196 [NOI2002] 银河英雄传说
题意:
有 N 艘战舰,依次编号为 1,2,…,N,其中第 i 号战舰处于第 i 列。
有 T 条指令,每条指令格式为以下两种之一:
M i j,表示让第 i 号战舰所在列的全部战舰保持原有顺序,接在第 j 号战舰所在列的尾部。
C i j,表示询问第 i 号战舰与第 j 号战舰当前是否处于同一列中,如果在同一列中,它们之间间隔了多少艘战舰。
编写程序处理一系列的指令。
思路:
维护两个战舰是否在同一列可以使用并查集。考虑如何维护战舰的位置。直接在并查集中链式维护显然会超时,可以记录每个节点到根节点的距离。合并时,把集合大小记在根节点上,把集合 A 合并到集合 B 上时,更新集合 B 的大小,并更新集合 A 根节点的距离等信息,这样在路径压缩时就能传递到其他节点上。
参考代码:
#include <iostream>
using namespace std;
// 1. 带权并查集的定义(用结构体保存节点)
struct node {
int fa, d, size;
#define fa(i) f[i].fa
#define d(i) f[i].d
#define size(i) f[i].size
} f[30005];
// 2. 带权并查集的路径压缩查询
int get(int x) {
if (fa(x) == x)
return x;
int root = get(fa(x));
d(x) += d(fa(x));
return fa(x) = root;
}
// 3. 带权并查集的合并(要维护根节点上的数据)
void merge(int x, int y) {
int fx = get(x), fy = get(y);
if (fx == fy)
return;
fa(fy) = fa(fx);
d(fy) = size(fx);
size(fx) += size(fy);
}
int t;
int main() {
ios::sync_with_stdio(0);
#ifndef ONLINE_JUDGE
freopen("data.in", "r", stdin);
freopen("data.out", "w", stdout);
#endif
// 4. 初始化带权并查集
for (int i = 1; i <= 30000; i++) {
fa(i) = i;
d(i) = 0;
size(i) = 1;
}
cin >> t;
while (t--) {
char op;
int i, j;
cin >> op >> i >> j;
if (op == 'M')
merge(j, i);
else {
if (get(i) != get(j))
cout << -1 << endl;
else
cout << abs(d(i) - d(j)) - 1 << endl;
}
}
return 0;
}
拓展域并查集
在同时维护多种关系时,考虑使用拓展域并查集。即把每一个元素拆成多个元素,放到不同的域中。
具体的实现方法是,比如全部 \(n\) 个元素拆成 \(2\) 个域,\(A\) 域和 \(B\) 域,则 \(A\) 域中的 \(i\) 可以用 \(i\) 表示, \(B\) 域中的 \(i\) 可以用 \(n + i\) 表示。
由此可见,将 \(n\) 个元素的集合拆成 \(k\) 个域,所用的空间是 \(O(nk)\)。
洛谷 P1892 [BOI2003]团伙
朋友关系具有传递性,可以使用并查集。
对于敌人关系,可以拓展一个敌人域,如果两个人互为敌人,那就分别把两人和敌人域中两人合并。
最后统计集合个数即可。
参考代码:
#include <iostream>
using namespace std;
const int N = 1005;
int f[2 * N], n, m, ans; // 分成 2 个域要开 2 倍空间
int get(int x) {
if (f[x] == x) return x;
return f[x] = get(f[x]);
}
void merge(int x, int y) {
f[get(x)] = get(y);
}
int main() {
ios::sync_with_stdio(0);
#ifndef ONLINE_JUDGE
freopen("data.in", "r", stdin);
freopen("data.out", "w", stdout);
#endif
cin >> n >> m;
for (int i = 1;i <= 2 * n;i++) f[i] = i;
for (int i = 1;i <= m;i++) {
char op; int p, q;
cin >> op >> p >> q;
if (op == 'F') merge(p, q);
else merge(n + p, q), merge(n + q, p);
}
for (int i = 1;i <= n;i++) if (f[i] == i) ans++;
cout << ans << endl;
return 0;
}
P2024 [NOI2001] 食物链
题意:
动物王国中有三类动物 A,B,C,这三类动物的食物链构成了有趣的环形:A 吃 B,B 吃 C,C 吃 A。
现有 \(N\) 个动物,以 \(1∼N\) 编号。每个动物都是 A,B,C 中的一种,但是我们并不知道它到底是哪一种。有人用两种说法对这 \(N\) 个动物所构成的食物链关系进行描述:
第一种说法,表示 X 和 Y 是同类。第二种说法表示 X 吃 Y。
此人对 \(N\) 个动物,用上述两种说法,一句接一句地说出 \(K\) 句话,这 \(K\) 句话有的是真的,有的是假的。 当一句话满足下列三条之一时,这句话就是假话,否则就是真话。
- 当前的话与前面的某些真的话冲突,就是假话;
- 当前的话中 X 或 Y 比 N 大,就是假话;
- 当前的话表示 X 吃 X,就是假话。
你的任务是根据给定的 \(N\) 和 \(K\) 句话,输出假话的总数。
思路:
本题可以用带权并查集或者拓展域并查集解决,这里讨论一下拓展域并查集解法。
食物链构成环形是解题的关键。这意味着如果 A 吃 B,那么 B 一定吃 C,C 一定吃 A。
考虑拓展域并查集,开捕食域与天敌域两个拓展域,加上原域总共需要三倍空间。如果 X 和 Y 是同类,那这句话是假话当且仅当 X 吃 Y 或者 Y 吃 X,不是假话则把三个域分部合并。X 吃 Y 是假话当且仅当 X 和 Y 是同类或者 Y 吃 X,不是假话也相应合并。具体代码实现细节如下:
#include <bits/stdc++.h>
using namespace std;
// #define int long long
const int N = 5e4;
int n, k;
int f[3 * N + 5];
#define eat(x) (x + N) // 捕食域
#define eaten(x) (x + N + N) // 天敌域
int find(int x) { return x == f[x] ? x : f[x] = find(f[x]); }
void merge(int x, int y) { f[find(x)] = find(y); }
int ans;
signed main()
{
ios::sync_with_stdio(0);
#ifdef DEBUG
clock_t t0 = clock();
freopen("data.in", "r", stdin);
freopen("data.out", "w", stdout);
#endif
// Don't stop. Don't hide. Follow the light, and you'll find tomorrow.
cin >> n >> k;
for (int i = 1; i <= n; i++)
f[i] = i, f[eat(i)] = eat(i), f[eaten(i)] = eaten(i);
while (k--)
{
int d, x, y;
cin >> d >> x >> y;
if (x > n || y > n)
{
ans++;
continue;
}
if (d == 1)
{
if (find(eat(x)) == find(y) || find(x) == find(eat(y)))
{
ans++;
continue;
}
merge(x, y), merge(eat(x), eat(y)), merge(eaten(x), eaten(y));
}
else
{
if (find(x) == find(y) || find(x) == find(eat(y)))
{
ans++;
continue;
}
merge(eat(x), y), merge(eaten(y), x), merge(eaten(x), eat(y)); // 最关键的是 eaten(x) 会吃 y
}
}
cout << ans << endl;
#ifdef DEBUG
cerr << "Time used:" << clock() - t0 << "ms" << endl;
#endif
return 0;
}
并查集在图论中的运用
并查集在图论中的应用主要是最小生成树和判断无向图的连通性。
图论部分我不熟悉,所以我将在图论学习笔记中记录这些内容。
参考资料 && 拓展阅读 && 推荐题目
- 《深入浅出程序设计竞赛(基础篇)》,洛谷学术组编著,17.1 并查集
- 《算法竞赛进阶指南》,李煜东著,0x41 并查集
- 洛谷日报 #87[喵小皮]浅谈并查集优化
- 洛谷 P2256 一中校运会之百米跑 提示:并查集+离散化/map
- 洛谷 P1551 亲戚 提示:并查集维护传递关系
- 洛谷 P1111 修复公路 提示:并查集+排序
- 洛谷 P8654 [蓝桥杯 2017 国 C] 合根植物 提示:统计并查集集合个数
- 洛谷 P3958 [NOIP2017 提高组] 奶酪 提示:并查集+数学
- 洛谷 P2814 家谱 提示:并查集+离散化/map
- 洛谷 P1455 搭配购买 提示:并查集+01背包


