【BZOJ3240】【UOJ#124】【NOI2013】矩阵游戏
终于看懂一道题QAQ然而NOI都是这种难度题怎么玩QAQ
原题：
婷婷是个喜欢矩阵的小朋友,有一天她想用电脑生成一个巨大的n行m列的矩阵(你不用担心她如何存储)。她生成的这个矩阵满足一个神奇的性质：若用F[i][j]来表示矩阵中第i行第j列的元素，则F[i][j]满足下面的递推式:
F[1][1]=1
F[i,j]=a*F[i][j-1]+b (j!=1)
F[i,1]=c*F[i-1][m]+d (i!=1)
递推式中a,b,c,d都是给定的常数。
现在婷婷想知道F[n][m]的值是多少,请你帮助她。由于最终结果可能很大，你只需要输出F[n][m]除以1,000,000,007的余数。
1<=N,M<=10^1000 000,a<=a,b,c,d<=10^9
恩显然数论
数论嘛，直接推公式
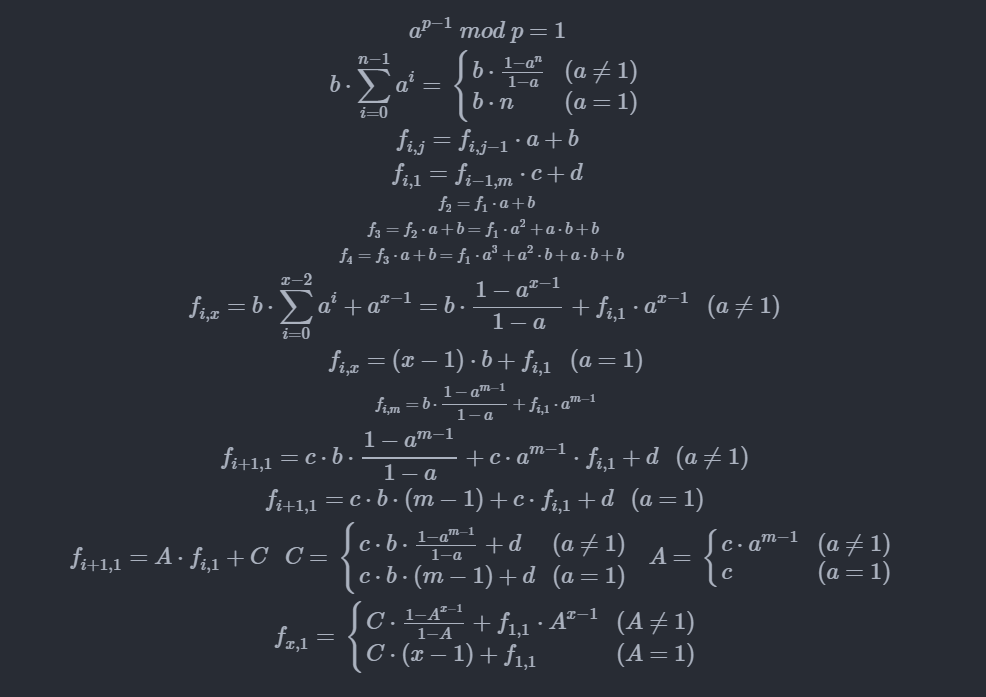
然后就可以一步算出来f[n][1]，然后再一步算出来f[n][m]即可
推推公式或许有奇迹hhh
（然而那个把f[i][1]推到f[i+1][1]的公式转化成C*（1-A^(x-1))/(1-A)+f[1][1]*A^(x-1)的形式似乎真的不好想出来QAQ
实现有许多细节，尤其是处理A是否等于1的时候容易写错
NOI都是这种难度的题怎么玩嘛QAQ
代码：
1 #include<iostream> 2 #include<cstdio> 3 #include<algorithm> 4 #include<cstring> 5 #include<cmath> 6 using namespace std; 7 #define ll long long 8 const int mo=(int)1e9+7; 9 int rd(){int z=0,mk=1; char ch=getchar(); 10 while(ch<'0'||ch>'9'){if(ch=='-')mk=-1; ch=getchar();} 11 while(ch>='0'&&ch<='9'){z=(z<<3)+(z<<1)+ch-'0'; ch=getchar();} 12 return z*mk; 13 } 14 char n[1100000],m[1100000]; 15 ll na=0,nb=0,ma=0,mb=0,a,b,c,d; ll C,A; 16 ll qcp(ll x,ll y){ 17 ll z=1,bs=x; 18 while(y){ if(y&1) z=(z*bs)%mo; bs=(bs*bs)%mo; y>>=1;} 19 return z; 20 } 21 ll x_1(ll x){ return qcp(x,mo-2);} 22 int main(){freopen("ddd.in","r",stdin); 23 scanf("%s%s",n,m); 24 int ln=strlen(n),lm=strlen(m); 25 for(int i=0;i<ln;++i) na=(na*10+n[i]-'0')%mo,nb=(nb*10+n[i]-'0')%(mo-1); 26 for(int i=0;i<lm;++i) ma=(ma*10+m[i]-'0')%mo,mb=(mb*10+m[i]-'0')%(mo-1); 27 if(na==0) na=mo; if(ma==0) ma=mo; if(nb==0) nb=mo-1; if(mb==0) mb=mo-1; 28 cin>>a>>b>>c>>d; 29 if(a!=1) C=(c*b%mo*(qcp(a,(mb-1))-1)%mo*x_1(a-1)%mo+d)%mo,A=c*qcp(a,(mb-1))%mo; 30 else C=(c*b%mo*(ma-1)%mo+d)%mo,A=c; 31 ll tmp; 32 if(A!=1) tmp=(C*(qcp(A,(nb-1))-1)%mo*x_1(A-1)%mo+qcp(A,(nb-1)))%mo; 33 else tmp=(C*(na-1)%mo+1)%mo; 34 ll ans; 35 if(a!=1) ans=(b*(qcp(a,(mb-1))-1)%mo*x_1(a-1)%mo+tmp*qcp(a,(mb-1))%mo)%mo; 36 else ans=((ma-1)*b%mo+tmp)%mo; 37 cout<<(ans%mo+mo)%mo<<endl; 38 //cout<<C<<" "<<A<<" "<<tmp<<endl; 39 return 0; 40 }
