【BZOJ1007】【HNOI2008】水平可见直线

依旧看黄学长代码，不过这回是看完后自己写的

原题：

 在xoy直角坐标平面上有n条直线L1,L2,...Ln,若在y值为正无穷大处往下看,能见到Li的某个子线段,则称Li为
可见的,否则Li为被覆盖的.
例如,对于直线:
L1:y=x; L2:y=-x; L3:y=0
则L1和L2是可见的,L3是被覆盖的.
给出n条直线,表示成y=Ax+B的形式(|A|,|B|<=500000),且n条直线两两不重合.求出所有可见的直线.

0 < N < 50000

 

给线段求下凸包，还算比较简单把

用栈，首先根据斜率排个序，这里建议如果斜率相等呢么y轴上截距递减，这样如果要插入的直线斜率和栈顶斜率相等直接停止就行了

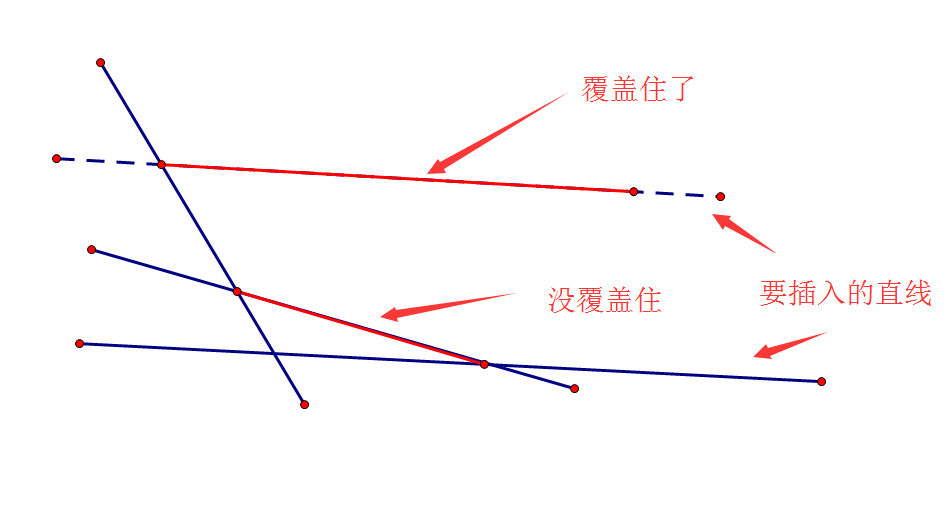
如果要插入的直线和栈中top-1的交点在栈中top和栈中top-2的交点的左边，呢么top--

为什么呐

手玩三条直线很容易看出来，图比较好画我就画一下吧（我也只能画简单的图了）

怎么计算交点呐

因为是很简单的x=kx+b，这就是小学数学，为了增加文章的篇幅来扯一扯 _(:3 」∠)_

就是解二元一次方程组，{y=k1x+b1,y=k2x+b2}，下面减上面，(k2-k1)x=b1-b2，x=(b1-b2)/(k2-k1)

然后随便搞一搞就行了，最后用bool记录答案来保证id递增

小技巧：fabs是计算浮点数的绝对值，注意fabs计算的并不是差的绝对值，也就是说应该是fabs(a-b)而不是fabs(a,b)，需要cmath

我看黄学长和另一个人的代码比x的时候都是直接<=，算时x返回是double啊不是不能直接=么，然而还是过了，不知道为什么

代码：

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
using namespace std;
int read(){int z=0,mark=1;  char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')mark=-1;  ch=getchar();}
    while(ch>='0'&&ch<='9'){z=(z<<3)+(z<<1)+ch-'0';  ch=getchar();}
    return z*mark;
}
bool deng(double x,double y){  return fabs(x-y)<1e-8;}//fabs传的是绝对值，所以不能fabs(a-b)
int n;  struct cdd{double k,b;  int id;}a[51000];//y=kx+b
bool compare(cdd x,cdd y){  return (deng(x.k,y.k)) ? (x.b>y.b) : (x.k<y.k);}
bool ans[51000];
cdd zhan[51000];  int top=0;
double get_x(cdd x,cdd y){  return (x.b-y.b)/(y.k-x.k);}
void insert(cdd x){
    if(deng(x.k,zhan[top].k))  return ;
    while(top>1 && get_x(x,zhan[top-1]) <= get_x(zhan[top],zhan[top-1]))  top--;
    zhan[++top]=x;
}
int main(){//freopen("ddd.in","r",stdin);
    memset(ans,0,sizeof(ans));
    cin>>n;
    for(int i=1;i<=n;i++)  scanf("%lf%lf",&a[i].k,&a[i].b),a[i].id=i;
    sort(a+1,a+n+1,compare);
    a[0].k=a[0].b=-999999999;
    for(int i=1;i<=n;i++)  insert(a[i]);
    for(int i=1;i<=top;i++)  ans[zhan[i].id]=true;
    for(int i=1;i<=n;i++)if(ans[i])  printf("%d ",i);
    cout<<endl;
    return 0;
}