代码随想录第十七天 | Leecode 654. 最大二叉树、617. 合并二叉树、700. 二叉搜索树中的搜索、98. 验证二叉搜索树

Leecode 654. 最大二叉树

题目描述

给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:

创建一个根节点，其值为 nums 中的最大值。
递归地在最大值 左边 的 子数组前缀上 构建左子树。
递归地在最大值 右边 的 子数组后缀上 构建右子树。
返回 nums 构建的 最大二叉树 。

• 示例 1：

输入：nums = [3,2,1,6,0,5]
输出：[6,3,5,null,2,0,null,null,1]

• 示例 2：

输入：nums = [3,2,1]
输出：[3,null,2,null,1]

递归建立最大二叉树

本题和昨天做过的构建二叉树的题目很像，甚至相比之下会更简单，构造树所需传入的数组只有一个。可以大致写出迭代算法的思路如下：

• 首先确定终止条件：当前数组为空时，则返回空指针
• 处理当前节点：找出数组中最大值的所在序号，根据最大值建立新节点
• 递归处理左右子节点
• 返回当前节点

根据上面思路可以得到代码如下：

class Solution {
public:
    TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
        if(nums.empty()) return nullptr; // 如果当前数组为空，则直接返回空指针
        int rootIndex = 0; // 初始化根节点序号
        for(int i = 0; i < nums.size(); i++){ // 遍历查找数组中最大值的序号，作为根节点的值
            if(nums[i] > nums[rootIndex]) rootIndex = i;
        }
        TreeNode* root = new TreeNode(nums[rootIndex]); // 新建节点，用最大数建立根节点
        vector<int> leftVec(nums.begin(), nums.begin() + rootIndex); // 将最大数左侧的数组作为新的数组，并递归建立左子树
        root->left = constructMaximumBinaryTree(leftVec);

        vector<int> rightVec(nums.begin()+rootIndex+1, nums.end()); // 将最大数右侧的数组作为新的数组，并递归建立右子树
        root->right = constructMaximumBinaryTree(rightVec);

        return root; // 返回根节点
    }
};

Leecode 617. 合并二叉树

题目描述

给你两棵二叉树： root1 和 root2 。

想象一下，当你将其中一棵覆盖到另一棵之上时，两棵树上的一些节点将会重叠（而另一些不会）。你需要将这两棵树合并成一棵新二叉树。合并的规则是：如果两个节点重叠，那么将这两个节点的值相加作为合并后节点的新值；否则，不为 null 的节点将直接作为新二叉树的节点。

返回合并后的二叉树。

注意: 合并过程必须从两个树的根节点开始。

• 示例 1：

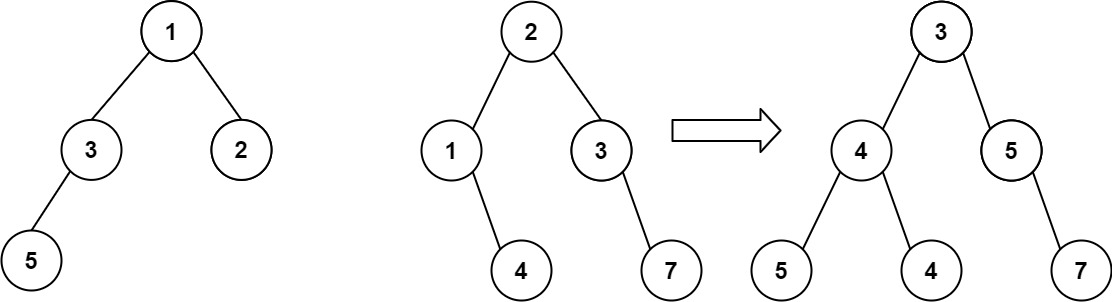
输入：root1 = [1,3,2,5], root2 = [2,1,3,null,4,null,7]
输出：[3,4,5,5,4,null,7]

• 示例 2：

输入：root1 = [1], root2 = [1,2]
输出：[2,2]

递归合并二叉树

本题使用递归进行合并，重点在于讨论终止条件：

• 如果当前两棵树的当前节点都为空，则返回空
• 如果有一棵树的当前节点为空，则直接返回另一棵树的根节点；后续子节点也相当于直接嫁接过来
• 如果都不为空，则当前节点为两棵树的节点值相加。并需要对当前节点的左右子节点进行递归

class Solution {
public:
    TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
        if(!root1 && !root2 )return nullptr; // 都为空返回空
        if(!root1) return root2; // 一个为空，直接嫁接另一棵树
        if(!root2) return root1;
        TreeNode* root = new TreeNode(root1->val + root2->val); // 都不为空，则需要将两棵树当前节点相加
        root->left = mergeTrees(root1->left, root2->left); // 递归合并左右子树
        root->right = mergeTrees(root1->right, root2->right);
        return root;
    }
};

Leecode 700. 二叉搜索树中的搜索

题目描述

给定二叉搜索树（BST）的根节点 root 和一个整数值 val。

你需要在 BST 中找到节点值等于 val 的节点。 返回以该节点为根的子树。 如果节点不存在，则返回 null 。

• 示例 1:

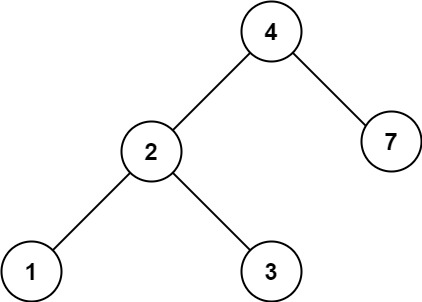
输入：root = [4,2,7,1,3], val = 2
输出：[2,1,3]

• 示例 2:

输入：root = [4,2,7,1,3], val = 5
输出：[]

递归法进行查找

在二叉树中进行查找非常方便快捷，只需要从根节点开始，如果值比当前节点更大；则往右子树查找，如果值更小则往左子树查找；但如果一直找到空节点都没有相等，则返回空。可以写出代码如下：

class Solution {
public:
    TreeNode* searchBST(TreeNode* root, int val) {
        if(!root) return nullptr;
        if(val > root->val) return searchBST(root->right, val);
        if(val < root->val) return searchBST(root->left, val);
        return root;
    }
};

Leecode 98. 验证二叉搜索树

题目描述

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效 二叉搜索树定义如下：

节点的左子树只包含 小于 当前节点的数。
节点的右子树只包含 大于 当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。

• 示例 1：

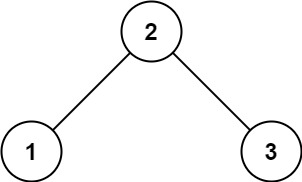
输入：root = [2,1,3]
输出：true

• 示例 2：

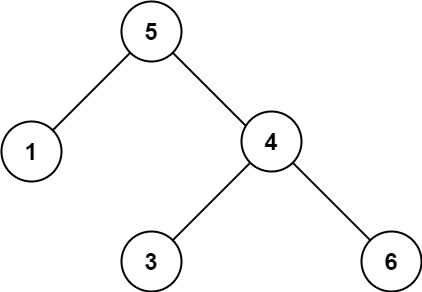
输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4。

使用递归进行验证

对于本题，首先需要明确二叉搜索树的定义，对于每一个节点，都必须满足比左子树中最大的节点更大，比右子树中最小的节点更小。需要特别注意的是，这里提到的最大和最小的节点，都并不一定直接是左右子节点，在不清楚二叉搜索树的定义的情况下，非常容易混淆这一点。如果仅仅只考虑每一个节点比左子节点大，比右子节点小，那么很容易写成下面这样：

// 错误示范
class Solution {
public:
    void isValidHelper(TreeNode* root, bool& isValid){
        if(!root || !isValid) return;
        if(root->left) { 
            if(root->left->val >= root->val){ // 仅与左子节点比较，正确应当是与左子树中的最大节点比较
                isValid = false; 
                return;
            }
            isValidHelper(root->left, isValid);
        }
        if(root->right) {
            if(root->right->val <= root->val){ // 仅与右子节点比较，正确应与右子树中的最小节点比较
                isValid = false;
                return;
            }
            isValidHelper(root->right,isValid);
        }
        return;
    }

    bool isValidBST(TreeNode* root) {
        bool isValid = true;
        isValidHelper(root, isValid);
        return isValid;
    }
};

上面代码无法通过测试算例，而把这段代码写下来也是为了给自己加深印象（因为我第一反应就是这样写的）。

正确的思路应当是采用中序遍历，实际上对于二叉搜索树的中序遍历，正好就是排序好的序列。所以只需要记录该二叉数的中序遍历序列，再判断序列是否满足单调递增性，即可判断该序列是否为二叉搜索树。但是，如果采用先建立中序遍历，后续再遍历一遍中序遍历是否满足单调递增性，所消耗的时间复杂度：中序遍历$O(\log n) + \(遍历数组\)O(n)\(，故总时间复杂度为\)O(n)\(。而如果可以在进行中序遍历的同时就能判断是否为二叉搜索树，就可以省略后续时间复杂度为\)O(n)$的遍历。因此我们可以得到代码如下：

class Solution {
public:
    void inOrder(TreeNode* curNode, vector<int>& orderVec, bool& result){ // 辅助函数，进行中序遍历，同时也要判断是否满足二叉搜索树
        if(!curNode || !result) return; // 如果当前节点为空，或者已经确定不是二叉搜索树，直接返回
        if(curNode->left) inOrder(curNode->left, orderVec, result); // 如果左子节点存在，则对左子节点递归调用
        if(orderVec.size() > 0 && orderVec[orderVec.size()-1] >= curNode->val)  { // 将当前节点与于已经记录的中序序列最后一个元素进行比较；如果记录为空，则不比较
            result = false; // 如果当前节点不大于左子树中最大节点，说明不是二叉搜索树，将result设置为false
            return;
        }
        orderVec.push_back(curNode->val); // 如果当前节点更大，则将当前节点记录到vector中
        if(curNode->right) inOrder(curNode->right, orderVec, result); // 对右子树递归调用
        return;
    }

    bool isValidBST(TreeNode* root) { 
        bool result = true; // 初始化result为真，后续判断如果不满足再变为false，如果遍历结束都还满足则为真
        vector<int> orderVec; // 初始化空的Vector，用于存放
        inOrder(root, orderVec, result); // 中序遍历，同时判断是否满足二叉搜索树的条件
        return result; // 返回结果
    }
};

上面判断代码的时间复杂度为\(O(n)\)。

今日总结

今天题目都比较简单，加深了对于二叉搜索树的定义的熟悉。

今天力扣刷到64题了，再接再厉！