代码随想录第三天 | Leecode 203. 移除链表元素、707. 设计链表、206. 翻转链表
Leecode 203 移除链表元素
题目描述
给你一个链表的头节点 head 和一个整数 val ,请你删除链表中所有满足 Node.val == val 的节点,并返回 新的头节点 。
-
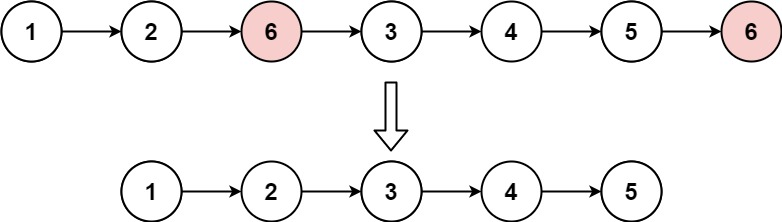
示例1
![]()
- 输入:
head = [1,2,6,3,4,5,6],val = 6 - 输出:
[1,2,3,4,5]
- 输入:
-
示例 2:
- 输入:
head = [], val = 1 - 输出:
[]
- 输入:
-
示例 3:
- 输入:
head = [7,7,7,7], val = 7 - 输出:
[]
- 输入:
解法1 单次遍历删除
本题要求删除链表中制定取值的所有节点,而链表中本身就是有删除操作定义的,即删除制定位置的元素。此时需要从链表头开始遍历走到这个节点的上一个节点,并将指针指向待删除节点的下一个节点,同时释放待删除节点的内存。所以对于本题有一个非常自然的算法思路:
- 从链表的头到尾进行遍历,同时判断当前节点的值是否与输入目标值相等
- 如果值相等,则调用链表的删除操作删去这个节点
- 如果值不相等,则遍历下一个节点
这个算法思路非常简单而自然,我们可以大致估算一下他的时间复杂度。每次进行删除操作需要从头节点开始遍历,故单次删除的时间复杂度为\(O(n)\),而从头到尾遍历有可能删除\(n\)个数量级的节点,即调用\(n\)次\(O(n)\)复杂度的操作,故该算法时间复杂度为\(O(n^2)\)。虽然这个时间复杂度较大,但是起码也是能够解决问题。接下来我们继续考虑能否仅用一次遍历就能完成整个操作。
一个降低时间复杂度的思想是:逐个遍历整个链表,遍历的同时做判断。如果需要删除,则直接在原地删除,而不必像刚才所说的调用删除操作还需要从头开始遍历一遍。但同时我们注意到,链表的删除操作需要能够拿到待删除节点的前一个节点,将前一个节点的next指向待删除节点的下一个节点,并释放待删除节点的内存。为了能够拿到待删除节点的上一个节点,那么我们可以有两种选择:
- 使用双指针法一起遍历链表,一个指针指向当前节点,另一个指针指向当前节点的上一个节点;如果当前节点需要删除,则可以利用上一个节点的指针。
- 还是使用一个指针来进行遍历,但是每次判断使用该指针的
next节点的val值,如果next节点需要删除,那么就将该指针的next指向原本next节点的next节点。但这种方法需要特别注意边界检查,因为如果遍历到了最后一个节点,此时的next节点为nullptr,而如果再调用此时“next节点的val值”,则有可能造成异常。
上面提到的这两种算法都是只用了一次遍历,在遍历的同时进行时间复杂度为\(O(1)\)的删除操作,故这两种算法的时间复杂度都是\(O(n)\)。
同时对于上面这两种算法都需要注意,如何处理第一个节点需要删除的情况。为此我的解决方案是先暂时不处理第一个节点,删除除第一个节点以外后续需要删除的所有节点之后,再来判断头节点是否需要删除。当然也可以使用虚拟节点的方式来表示头节点,这样删除每一个节点的操作都是一模一样的了。
在这里我们给出仅用一个指针的单次遍历删除的代码:
class Solution {
public:
ListNode* removeElements(ListNode* head, int val) {
if(head == nullptr){ // 处理空链表的特殊情况,避免后续直接访问头节点的next出现异常
return nullptr;
}
ListNode* cur = head; // 从当前节点初始化
while(cur->next != nullptr){ // 如果下一个节点非空,则需要进行判断
if(cur->next->val == val){ // 若下一个节点需要删除
ListNode* toDelete = cur->next; // 进行删除操作
cur->next = cur->next->next;
delete toDelete;
}
else{
cur = cur->next; // 如果不用删除,才遍历到下一个节点
}
}
if(head->val == val){ // 最后来处理头节点是否需要删除
ListNode* newHead = head->next;
delete head;
return newHead;
}
return head;
}
};
解法2 使用递归
本题也可以考虑使用递归的方式来求解。我们可以节整条链表看做是两部分,左边一部分看做是已经删除过待删除元素的链表,而右侧则是还未处理过的链表。初始情况相当于左侧已经处理过的链表长度为0,而右侧未处理的则是原始输入的链表。每一次对右侧链表进行操作,可以看做是一模一样的问题,可以直接通过调用递归函数来进行递归。由此我们可以得到下面的递归算法框架:
- 递归函数(链表头节点,待删除的值)
- 递归终止条件:如果当前头节点已经为空,说明已经删除完毕,直接返回
- 判断头节点的情况来进行处理,并调用递归函数:
- 如果当前头节点需要删除,则执行删除操作,并调用递归,使下一个节点作为后续链表的头节点
- 如果当前节点不需要删除,则直接调用递归,使下一个节点作为后续链表的头节点
通过上面的递归算法,就可以很轻松地解决这个问题,我们可以得到代码如下:
class Solution {
public:
ListNode* removeElements(ListNode* head, int val) {
if(head == nullptr){ // 递归终止条件,如果头节点已经为空,说明待处理的链表已经为空,直接返回
return nullptr;
}
if(head->val == val){ // 如果当前头节点需要删除
ListNode* newNode = head->next; // 则进行删除操作
delete head;
return removeElements(newNode,val); // 并返回下一个节点作为新的头节点
}
else{ // 如果当前头节点不需要删除
head->next = removeElements(head->next,val); // 则调用递归,令下一个节点作为后续已经处理过的链表的头节点
return head; // 返回头节点
}
}
};
我们可以分析这段递归代码的时间复杂度,其实就是对每一个节点都当做头节点来进行了一次判断,并处理相应操作。其实也就相当于将整个链表中的节点都遍历了一次,故时间复杂度为\(O(n)\)。
Leecode 707 设计链表
题目描述
你可以选择使用单链表或者双链表,设计并实现自己的链表。
单链表中的节点应该具备两个属性:val 和 next 。val 是当前节点的值,next 是指向下一个节点的指针/引用。
如果是双向链表,则还需要属性 prev 以指示链表中的上一个节点。假设链表中的所有节点下标从 0 开始。
实现 MyLinkedList 类:
-
MyLinkedList()初始化MyLinkedList对象。 -
int get(int index)获取链表中下标为index的节点的值。如果下标无效,则返回-1。 -
void addAtHead(int val)将一个值为val的节点插入到链表中第一个元素之前。在插入完成后,新节点会成为链表的第一个节点。 -
void addAtTail(int val)将一个值为val的节点追加到链表中作为链表的最后一个元素。 -
void addAtIndex(int index, int val)将一个值为val的节点插入到链表中下标为index的节点之前。如果index等于链表的长度,那么该节点会被追加到链表的末尾。如果index比长度更大,该节点将 不会插入 到链表中。 -
void deleteAtIndex(int index)如果下标有效,则删除链表中下标为index的节点。 -
示例:
- 输入
["MyLinkedList", "addAtHead", "addAtTail", "addAtIndex", "get", "deleteAtIndex", "get"] [[], [1], [3], [1, 2], [1], [1], [1]]- 输出
[null, null, null, null, 2, null, 3]
- 输入
-
解释:
MyLinkedList myLinkedList = new MyLinkedList();myLinkedList.addAtHead(1);myLinkedList.addAtTail(3);myLinkedList.addAtIndex(1, 2); // 链表变为 1->2->3myLinkedList.get(1); // 返回 2myLinkedList.deleteAtIndex(1); // 现在,链表变为 1->3myLinkedList.get(1); // 返回 3
题目思路
很无聊的一道题,考虑使用一个虚拟头节点来建立链表。同时逐个写完这些运算即可,没太多好说的,下面直接给出代码
class MyLinkedList {
private:
struct LinkNode {
int val;
LinkNode* next;
LinkNode(int x) : val(x), next(nullptr) {}
};
LinkNode* _dummyHead; // 虚拟头节点
int _size; // 链表长度
public:
// 构造函数:初始化虚拟头节点和长度
MyLinkedList() : _dummyHead(new LinkNode(0)), _size(0) {}
// 析构函数:释放所有节点
~MyLinkedList() {
LinkNode* cur = _dummyHead;
while (cur != nullptr) {
LinkNode* tmp = cur;
cur = cur->next;
delete tmp;
}
}
int get(int index) {
if (index < 0 || index >= _size) return -1; // 处理找不到的情况
LinkNode* cur = _dummyHead->next; // 从头节点的下一个节点开始
for (int i = 0; i < index; i++) { // 查找到相应序号的节点
cur = cur->next;
}
return cur->val;
}
void addAtHead(int val) {
LinkNode* newNode = new LinkNode(val); // 新建节点并初始化
newNode->next = _dummyHead->next; // 新节点指向原本头节点
_dummyHead->next = newNode; // 虚拟头节点指向新节点
_size++; // 更新链表长度
}
void addAtTail(int val) {
LinkNode* cur = _dummyHead; // 新建一个节点指针
while (cur->next != nullptr) { // 遍历直至最后一个节点
cur = cur->next;
}
cur->next = new LinkNode(val); // 在最后插入一个节点
_size++; // 链表长度+1
}
void addAtIndex(int index, int val) {
if (index > _size) return; // 处理如果找不到该序号的异常情况,直接返回
LinkNode* cur = _dummyHead; // 新建一个指针,注意此时是在虚拟头节点处
for (int i = 0; i < index; i++) { // 从虚拟头节点往后走index步,此时cur指向index个节点的前一个节点
cur = cur->next;
}
LinkNode* newNode = new LinkNode(val); // 新建一个节点
newNode->next = cur->next; // 新节点指向链表后续的元素
cur->next = newNode; // 用cur指向新节点(注意cur是index节点的前一个节点)
_size++; // 链表长度+1
}
void deleteAtIndex(int index) {
if (index < 0 || index >= _size) return; // 处理输入异常情况,直接返回
LinkNode* cur = _dummyHead; // cur从虚拟头节点开始
for (int i = 0; i < index; i++) { // cur往后遍历index步,指向节点为index节点的前一个节点
cur = cur->next;
}
LinkNode* toDelete = cur->next; // 删除index节点
cur->next = cur->next->next;
delete toDelete;
_size--; // 链表长度-1
}
};
本题并没有太多思维量,但是比较麻烦(毕竟要写这么多函数)。个人感觉最难的地方在于在类中建立struct结构,写构造函数和析构函数,以及对成员变量的声明。由于对面向对象还不是很熟练,所以其实还花了不少时间在设置变量这上面。可能还有一个难点在于如果使用虚拟头节点的情况下,在index处插入、删除需要遍历多少步;只要注意从虚拟头节点出发需要多走一步,同时要对index处的节点进行操作需要少走一步到其前一个节点;同时考虑这两个点那就不会错了。
Leecode 206 反转链表
题目描述
给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。
-
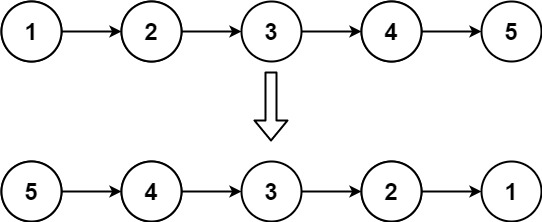
示例 1:
![]()
- 输入:
head = [1,2,3,4,5] - 输出:
[5,4,3,2,1]
- 输入:
-
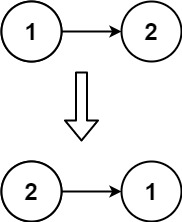
示例 2:
![]()
- 输入:
head = [1,2] - 输出:
[2,1]
- 输入:
-
示例 3:
- 输入:
head = [] - 输出:
[]
- 输入:
解法1 双指针遍历翻转(或者应该叫三指针?)
这道题我第一反应的算法是要新建一个链表,每次遍历取出当前链表的最后一个元素,然后插入到新链表中作为头节点。这种算法当然可以解决这个问题,但是新建链表需要消耗额外的空间。同时每一次取最后一个节点的操作的时间复杂度为\(O(n)\),那么依次取出所有的\(n\)个节点插入新链表中,所用的总时间复杂度就应该是\(O(n^2)\)。所以这当然是一个很差的算法。为此我们需要考虑能够仅用多个指针一次遍历就能达到我们的目标。
首先,链表麻烦的一个点在于,每个节点只能取到自己的下一个节点。而如果需要对其进行增、删操作,都需要该节点的上一个节点的参与。而如果每次都从头遍历一次直至当前节点的上一个节点,那么显然这个过程会消耗很多无用的时间复杂度。一个自然的想法就是同时用多个指针进行遍历,那么就可以同时取到链表中节点的上一个节点了。同时,对于本题而言,翻转链表也没有必要重新建一个链表,每个节点只需“原地掉头”即可。而这个“掉头”操作其实只需要将其自身的指针指向原本的上一个节点即可,但是为了进行这个“掉头”操作,我们还需要一些额外的注意事项:
- 对节点进行掉头,即直接将节点的指针指向其上一个节点,需要:
- 有指向当前节点的指针
cur - 有一个指向原本上一个节点的指针
pre,这样才能直接修改当前节点的指针(否则必须从头进行一次\(O(n)\)复杂度的遍历) - 有一个指向原本下一个节点的指针
temp,这样才能使得后续的链表不丢失,还能继续访问。也方便后续继续进行遍历
- 有指向当前节点的指针
根据上面分析可知,要想完成“原地掉头的操作”,我们需要三个指针,同时具体的掉头演示动画如下所示(其实我做这道题花的时间最久的在画下面这个动图上):

相信根据上面这个演示动画能够很容易地看出链表中每个元素依次“掉头”的过程,同时我们可以给出具体的代码如下所示
class Solution {
public:
ListNode* reverseList(ListNode* head) {
ListNode* pre = nullptr; // 记录上一个节点
ListNode* cur = head; // 记录当前节点
ListNode* temp; // 记录下一个节点,用于使得节点cur返回原链表
while(cur){
temp = cur->next; // 记录下一个节点
cur->next = pre; // 节点“掉头”
pre = cur; // pre和cur往下一个节点遍历
cur = temp;
}
return pre; // 返回已经翻转完成的链表的头节点
}
};
上面代码对照着图一起看还是很清晰的,代码中的每一步操作都对应了图中的一次移动。
解法2 递归法
(今天花太多时间学怎么画图了,这部分等之后有空再来补)
今日总结
感觉今天最大的收获就是学会了怎么用python里的manim来画图,虽然绘制上面图像的主要代码都是让AI辅助着写的,但是AI输出的结果还是一直都有一些错误。没办法我只能一点一点理解这个完全没用过的manim包里的方法。花了好几个小时才慢慢调对代码最后画出来了这版3b1b风格的动画hh。不得不说这个图画出来的感觉比我刷出算法题爽多了,还是挺有成就感的。
p.s. 通过今天画的这个图,我现在感觉我这辈子都忘不了翻转链表需要哪几步操作了。。。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号