多项式学习笔记（一）（2024.7.6）

声明：在本节范围内，所有同余号（多项式运算）均在$(\text{mod } x^n)$意义下进行；所有等号（代数运算）均在模某个质数$p$意义下进行。

暴力多项式计算

加法

$H(x) = F(x) + G(x)$，求$H(x)$

解：类比高精度加法

$h_i = f_i + g_i$，复杂度$O(n)$

#include <bits/stdc++.h>
using namespace std;
const int N = 209;
int lenf, f[N];
int leng, g[N];
int lenh, h[N];
int main (){
	scanf("%d", &lenf);
   scanf("%d", &leng);
   lenf++;
   leng++;
	for(int i = lenf; i >= 1; i--)
		scanf("%d", &f[i]);
	for(int i = leng; i >= 1; i--)
		scanf("%d", &g[i]);
	lenh = max(leng, lenf);	
	for(int i = 1; i <= lenh; i++)
		h[i] = f[i] + g[i];   
	for(int i = lenh; i >= 1; i--)
		printf("%d ", h[i]);
	return 0 ;
}

乘法

$H(x) \equiv F(x)G(x) (\text{mod }x^n)$，求$H(x)$

解：类比高精度乘法，复杂度$O(n^2)$

#include <bits/stdc++.h>
using namespace std;
const int N = 109;
int f[N], g[N], h[2 * N], lenf, leng, lenh;
int main(){
	scanf("%d", &lenf);
 	scanf("%d", &leng);
 	lenf++;
 	leng++;
	for(int i = lenf; i >= 1; i--)
		scanf("%d", &f[i]);
	for(int i = leng; i >= 1; i--)
		scanf("%d", &g[i]);
	for(int i = 1; i <= lenf; ++i){
        for(int j = 1; j <= leng; ++j){
        	int yx = i + j - 1;
          h[yx] += f[i] * g[j];
        }
	}	
    lenh = lenf + leng;
    for(int i = lenh; i >= 1; --i)
		printf("%d", h[i]);
	return 0;
}

求逆

$F(x)G(x) \equiv 1 (\text{mod }x^n)$

求$G(x)$

解：设$H(x) \equiv F(x)G(x)(\text{mod }x^n)$

$\therefore h_i = \displaystyle\sum_{j=0}^if_jg_{i-j}$(多项式乘法)

$\because H(x)$除了第$0$项是$1$其他都为$0$。

$\therefore \displaystyle\sum_{j=0}^if_jg_{i - j} = [i = 0]$

所有的$f_i$已知，那问题就转化成了求一个$n$元一次方程组的问题，用高斯消元即可。

除法/取模

$F(x)\equiv Q(x)G(x)+R(x)(\text{mod }{x^n})$

求$Q(x),R(x)$

解类比高精度除法，复杂度$O(n^2)$

#include <bits/stdc++.h>
using namespace std;
const int N = 1000;
int f[N], g[N], q[N], temp[N], lenf, leng, lenq;
int compare(int f[],int g[]){
    if(lenf > leng)
        return 1;
    if(lenf < leng)
        return -1;
    for(int i = lenf; i > 0; i--){  
        if(f[i] > g[i])
            return 1;
        if(f[i] < g[i])
            return -1;
    }
    return 0;
}
void subduction(int f[],int g[]){
    int flag;
    int i;
    flag = compare(f, g);
    if(flag == 0){
        lenf = 0;
        return;
    }
    if(flag == 1){
        for(int i = 1; i <= lenf; i++){
            if(f[i] < g[i]){
                f[i + 1]--;
                f[i] += 10;
            }
            f[i] -= g[i];
        }
        while(lenf > 0 && f[lenf] == 0)
            lenf--;
        return;
    }
}
int main(){
	scanf("%d", &lenf);
	scanf("%d", &leng);
	lenf++;
 	leng++;
	for(int i = lenf; i >= 1; i--)
		scanf("%d", &f[i]);
	for(int i = leng; i >= 1; i--)
		scanf("%d", &g[i]);
    lenq = lenf - leng + 1;
    for(int i = lenq; i > 0; i--){
        memset(temp, 0, sizeof(temp));
        for(int j = 1; j <= leng; j++)
            temp[j + i - 1] = g[j];
        temp[0] = leng + i - 1;
        while(compare(f, temp) >= 0){
            q[i]++;
            subduction(f, temp);
        }
    }
    while(lenq > 0 && q[lenq] == 0)
        lenq--;
    if(lenq == 0)
        printf("0\n");
    else{
        for(int i = lenq; i > 0; i--)
			printf("%d ", q[i]);
        printf("\n");
    }
    if(lenf == 0)
        printf("0\n");
    else{
        for(int i = lenf; i > 0; i--)
			printf("%d ", f[i]);
        printf("\n");
    }
    return 0;  
}

求导/积分

前置知识：求导及其特性

1、定义：$f'(x) = \mathop{lim}\limits_{\triangle x \rightarrow 0}\displaystyle\frac{f(x + \triangle x) - f(x)}{\triangle x}$

也可以说导数表示过函数上任意一点的切线斜率

2、性质：①$[f(x) + g(x)]' = \mathop{lim}\limits_{\triangle x \rightarrow 0}\displaystyle\frac{f(x + \triangle x) + g(x + \triangle x)- f(x) - g(x)}{\triangle x} = \mathop{lim}\limits_{\triangle x \rightarrow 0}\displaystyle\frac{f(x + \triangle x) - f(x)}{\triangle x} + \mathop{lim}\limits_{\triangle x \rightarrow 0}\displaystyle\frac{g(x + \triangle x) - g(x)}{\triangle x} = f'(x) + g'(x)$

②$[f(x)g(x)]'= \mathop{lim}\limits_{\triangle x \rightarrow 0}\displaystyle\frac{f(x + \triangle x)g(x + \triangle x)- f(x)g(x)}{\triangle x} = \mathop{lim}\limits_{\triangle x \rightarrow 0}\displaystyle\frac{f(x + \triangle x)g(x + \triangle x) - f(x + \triangle x)g(x) + f(x + \triangle x)g(x) - f(x)g(x)}{\triangle x} = \mathop{lim}\limits_{\triangle x \rightarrow 0}\displaystyle\frac{f(x + \triangle x)[g(x + \triangle x) - g(x)] + g(x)[f(x + \triangle x) - f(x)]}{\triangle x} = f(x)g'(x) + f'(x)g(x)$

③复合函数求导：$[f(g(x))]' = f'g(x)g'(x)$(目前不会证明)

3、特殊函数求导：

①$f'(x^n) = nx^{n - 1}$

②$f'(n^x) = n^x \text{ln }n$

③$f'(e^x) = e^x$

④$f'(\text{ln } x) = x^{-1}$

⑤$f'(\text{sin } x) = \text{cos } x$

⑥$f'(\text{cos } x) = -\text{sin } x$

前置知识：不定积分及其特性

1、定义：若$g'(x) = f(x)$，则$\displaystyle\int f(x)dx = g(x) + C$(加常数是因为求导时会将常数项减掉)

也可以说不定积分表示函数与$x$轴之间的面积

2、性质：$\displaystyle\int [f(x) + g(x)]dx = \displaystyle\int f(x)dx + \displaystyle\int g(x)dx$(目前不会证明)

3、特殊函数不定积分：

①$\displaystyle\int f(x^n)dx = \displaystyle\frac{x^{n + 1}}{n + 1} + C$

②$\displaystyle\int f(n^x)dx = \displaystyle\frac{1}{\text{ln }a} + C$

③$\displaystyle\int f(e^x)dx = e^x + C$

④$\displaystyle\int f(\displaystyle\frac{1}{x})dx = \text{ln x} + C$

⑤$\displaystyle\int f(\text{sin } x)dx = -\text{cos } x + C$

⑥$\displaystyle\int f(\text{cos } x)dx = \text{sin }x + C$

正题

$G(x) = F'(x)$

$H(x) = \displaystyle\int F(x)dx$

求$G(x),H(x)$

解：$F(x) = \displaystyle\sum_{i=0}^{n - 1}f_ix^i$(将多项式展开)

$F'(x) = \displaystyle\sum_{i=1}^{n - 1}f_i \cdot i \cdot x^{i - 1}$(特殊函数求导①) $= \displaystyle\sum_{i=0}^{n - 2}f_{i + 1} \cdot (i + 1) \cdot x^{i}$(用$i + 1$替换$i$)

又$\because G(x) = \displaystyle\sum_{i=0}^{n - 1}g_ix^i$(将多项式展开)，第$x^i$项系数应该相同

$\therefore g_i = f_{i + 1} \cdot (i + 1)$

运用求$G(x)$的公式，则有$f_i = h_{i + 1} \cdot (i + 1)$

$\therefore h(i + 1) = \displaystyle\frac{f_i}{i + 1}$(移项)

$\therefore h(i) = \displaystyle\frac{f_{i - 1}}{i}$(用$i$替换$i + 1$)

开根

$G^2(x) \equiv F(x)(\text{mod }{x^n})$

求$G(x)$

解：运用暴力多项式乘法的公式，则有$f_i = \displaystyle\sum_{j=0}^{i}g_jg_{i - j} = 2g_0g_i + \displaystyle\sum_{j=1}^{i - 1}g_jg_{i - j}$

$\therefore g_i = \displaystyle\frac{f_i - \displaystyle\sum_{j=1}^{i - 1}g_jg_{i - j}}{2g_0}$

$\because$求$g_i$时已求出$g_0$到$g_{i - 1}$

$\therefore$可以递推求出$G(x)$

注意 $g_0^2=f_0$ 是边界情况：

若 $f_0\neq0$，则$G$的解数，取决于$f_0$的平方根数量。
若 $f_0=0$，令 $F(x) = x^kH(x)$，满足 $h(0) \neq 0$，那么若$k$为奇数，则$G$无解；若$k$为偶数，记 $P^2(x) = H(x)$，那么 $G(x) = x^{\frac k2}P(x)$。

对数函数

$G(x) \equiv \text{ln }F(x)(\text{mod } x^n)$，保证$f_0 = 1$

求$G(x)$

解：对原等式两边求导，得：$G'(x) \equiv F'(x)F^{-1}(x)(\text{mod } x^n)$(复合函数求导)

令$H(x) \equiv F^{-1}(x)(\text{mod } x^n)$(多项式求逆)

$\therefore G(x) \equiv F'(x)H(x)(\text{mod } x^n)$

$\therefore (i + 1)g_{i + 1}=\displaystyle\sum_{j=0}^i{(j + 1)f_{j + 1}h_{i - j}}, g_0 = 0$

指数函数

$G(x) \equiv e^{F(x)}(\text{mod } x^n)$，保证$f_0 = 0$

求：$G(x)$

解：对原等式两边求导，得：$G'(x) \equiv F'(x)e^{F(x)}$(复合函数求导) $\equiv F'(x)G(x)(\text{mod } x^n)$

$\therefore (i + 1)g_{i + 1} = \displaystyle\sum_{j=0}^i{(j + 1)f_{j + 1}g_{i - j}}$

$\because$求$g_{i + 1}$时已求出$g_0$到$g_i$，且$g_0 = 1$

$\therefore$可以递推求出$G(x)$

三角函数

前置知识：泰勒级数与泰勒展开

$\because$求导操作会将常数项消掉，将其它项次数减1。

$\therefore$如果两个函数$F(x), G(x)$满足$\left\{ \begin{array}{lr} G(0) = F(0)\\ G'(0) = F'(0)\\ G^{(2)}(0) = F^{(2)}(0)\\ \dots \dots\\ G^{(+\infty)}(0) = F^{(+\infty)}(0) \end{array} \right.$

那么就可以说明，两个函数相等。($G^{(i)}(0) = F^{(i)}(0)$ 实际上表示$i!g_i = i!f_i$)

$\therefore$一个函数$F(x) = \displaystyle\sum_{i=0}^{+\infty}f_ix^i$可以表示为$\displaystyle\sum_{i=0}^{+\infty}\displaystyle\frac{F^{(i)}(0)}{i!}x^i$

$\because \text{sin }x = \text{sin }x$

$\text{sin}'\text{ }x = \text{cos }x $

$\text{sin}^{(2)}\text{ }x = -\text{sin }x$

$\text{sin}^{(3)}\text{ }x = -\text{cos }x$

$\text{sin}^{(4)}\text{ }x = \text{sin }x$(特殊函数求导⑤、⑥)

$\because \text{sin }x$在$x = 0$处的取值为$0$

$\therefore x^0$项的系数是$\displaystyle\frac{0}{0!} = 0$

$\because \text{cos }x$在$x = 0$处的取值为$1$

$\therefore x$项的系数是$\displaystyle\frac{1}{1!}$

$\because \text{-sin }x$在$x = 0$处的取值为$0$

$\therefore x ^ 2$项的系数是$\displaystyle\frac{0}{2!} = 0$

$\because \text{-cos }x$在$x = 0$处的取值为$-1$

$\therefore x^3$项的系数是$\displaystyle\frac{-1}{3!}$

一直循环下去，则有$\text{sin }x = \displaystyle\frac 1{1!}x + \displaystyle\frac{-1}{3!}x^3 + \displaystyle\frac1{5!}x^5 + \displaystyle\frac{-1}{7!}x^7 + \dots \dots$

同理：$\because \text{cos }x = \text{cos }x$

$\text{cos}'\text{ }x = -\text{sin }x $

$\text{cos}^{(2)}\text{ }x = -\text{cos }x$

$\text{cos}^{(3)}\text{ }x = \text{sin }x$

$\text{cos}^{(4)}\text{ }x = \text{cos }x$(特殊函数求导⑤、⑥)

$\because \text{cos }x$在$x = 0$处的取值为$1$

$\therefore x^0$项的系数是$\displaystyle\frac{1}{0!}$

$\because \text{-sin }x$在$x = 0$处的取值为$0$

$\therefore x$项的系数是$\displaystyle\frac{0}{1!} = 0$

$\because \text{-cos }x$在$x = 0$处的取值为$-1$

$\therefore x ^ 2$项的系数是$\displaystyle\frac{-1}{2!}$

$\because \text{sin }x$在$x = 0$处的取值为$0$

$\therefore x^3$项的系数是$\displaystyle\frac{0}{3!} = 0$

一直循环下去，则有$\text{cos }x = \displaystyle\frac 1{0!}x^0 + \displaystyle\frac{-1}{2!}x^2 + \displaystyle\frac1{4!}x^4 + \displaystyle\frac{-1}{6!}x^6 + \dots \dots$

同理：$\because e^{ix} = e^{ix}$

$(e^{ix})' = ie^{ix}$

$(e^{ix})^{(2)} = -e^{ix}$

$(e^{ix})^{(3)} = -ie^{ix}$

$(e^{ix})^{(4)} = e^{ix}$(复合函数求导)

$\because e^{ix}$在$x = 0$处的取值为$1$

$\therefore x^0$项的系数是$\displaystyle\frac{1}{0!}$

$\because ie^{ix}$在$x = 0$处的取值为$i$

$\therefore x$项的系数是$\displaystyle\frac{i}{1!}$

$\because -e^{ix}$在$x = 0$处的取值为$-1$

$\therefore x ^ 2$项的系数是$\displaystyle\frac{-1}{2!} = 0$

$\because -ie^{ix}$在$x = 0$处的取值为$-i$

$\therefore x^3$项的系数是$\displaystyle\frac{-i}{3!}$

一直循环下去，则有$e^{ix} = \displaystyle\frac 1{0!}x^0 + \displaystyle\frac i{1!}x + \displaystyle\frac{-1}{2!}x^2 + \displaystyle\frac {-i}{3!}x^3 + \displaystyle\frac1{4!}x^4 + \displaystyle\frac i{5!}x^5 + \displaystyle\frac{-1}{6!}x^6 + \displaystyle\frac {-i}{7!}x^7 + \dots \dots = \text{cos }x + i\text{sin }x$①

~~于是就有了大名鼎鼎的欧拉公式~~

于是$e^{-ix} = \text{cos }x - i\text{sin }x$②

① $+$ ② 得：$2\text{cos }x = e^{ix} + e^{-ix}$

$\text{cos }x = \displaystyle\frac{e^{ix} + e^{-ix}}2$

① $-$ ② 得：$2i\text{sin }x = e^{ix} - e^{-ix}$

$\text{sin }x = \displaystyle\frac{e^{ix} - e^{-ix}}{2i}$

正题

$G(x) = \text{sin }F(x)$

$H(x) = \text{cos }F(x)$

求$G(x),H(x)$

直接把$F(x)$带进公式，利用多项式指数函数算法即可。

若$i$在模$p$意义下有对应的数，那么可以直接用这个数来运算。

否则可以扩域，复杂度都是 $O(n^2)$。

快速傅里叶变换FFT

前置知识：多项式插值

$n+1$个横坐标互不相同的点可以唯一确定一个$n$次多项式。

证明：我还不会证，按照两点确定一条直线和三点确定一条抛物线类比吧qwq

前置知识：复数运算

复数是形如 $a+bi$ 的数，其中 $i^2=-1$，$a,b\in\mathbb{R}$。

复数运算：加：$(a + bi) + (c + di) = (a + c) + (b + d)i$

乘：$(a + bi)(c + di) = ac - bd + (ad + bc)i$

除：$\displaystyle\frac{a + bi}{c + di} = \displaystyle\frac{ac + bd + (bc - ad)i}{c^2 + d^2}$

前置知识：向量运算

如果将复数$a + bi$看成是一条从$(0, 0)$指向$(a, b)$的向量，将复数$c + di$看成是一条从$(0, 0)$指向$(c, d)$的向量，就可以研究向量的加减

向量运算：加：以两条向量为邻边，以两条向量劣角夹角为平行四边形的锐角顶点，做平行四边形，则两向量所夹对角线即为新向量，如图：

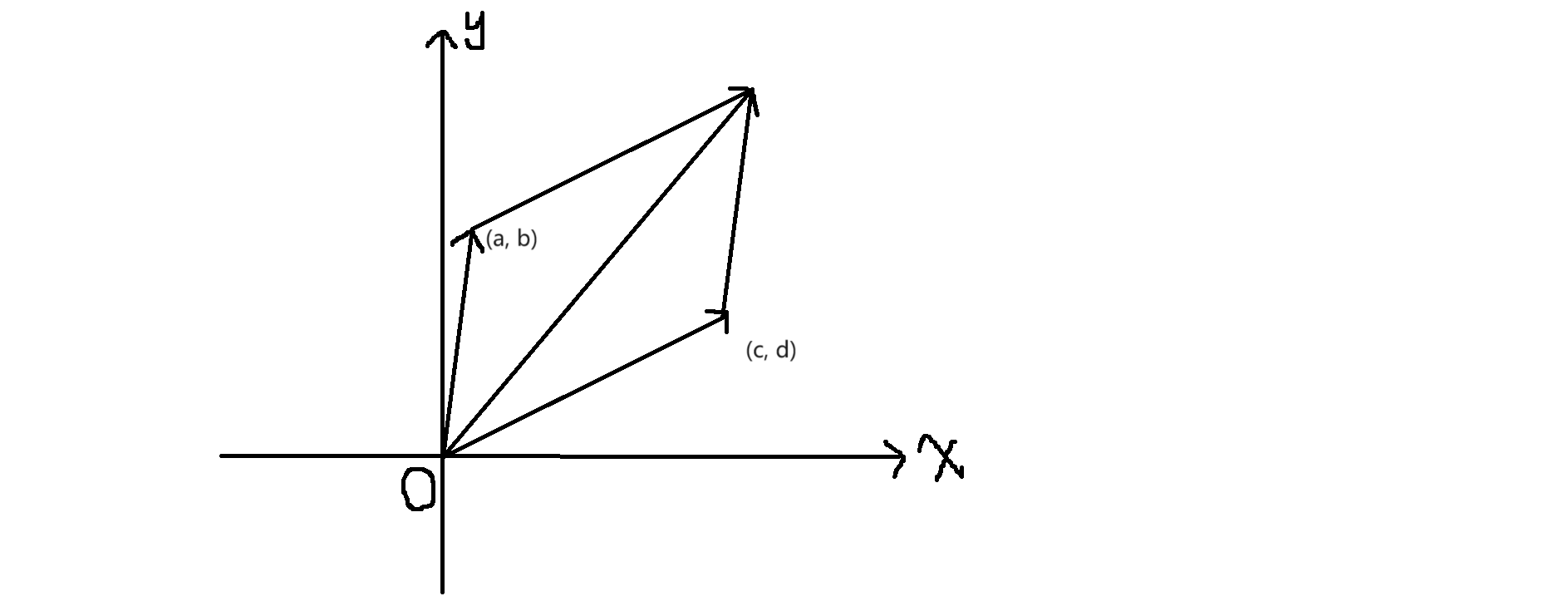
乘：将两条向量的模长相乘作为新向量的模长，将两条向量与$x$轴的顺时针夹角相加作为新向量与$x$轴的顺时针夹角，如图：

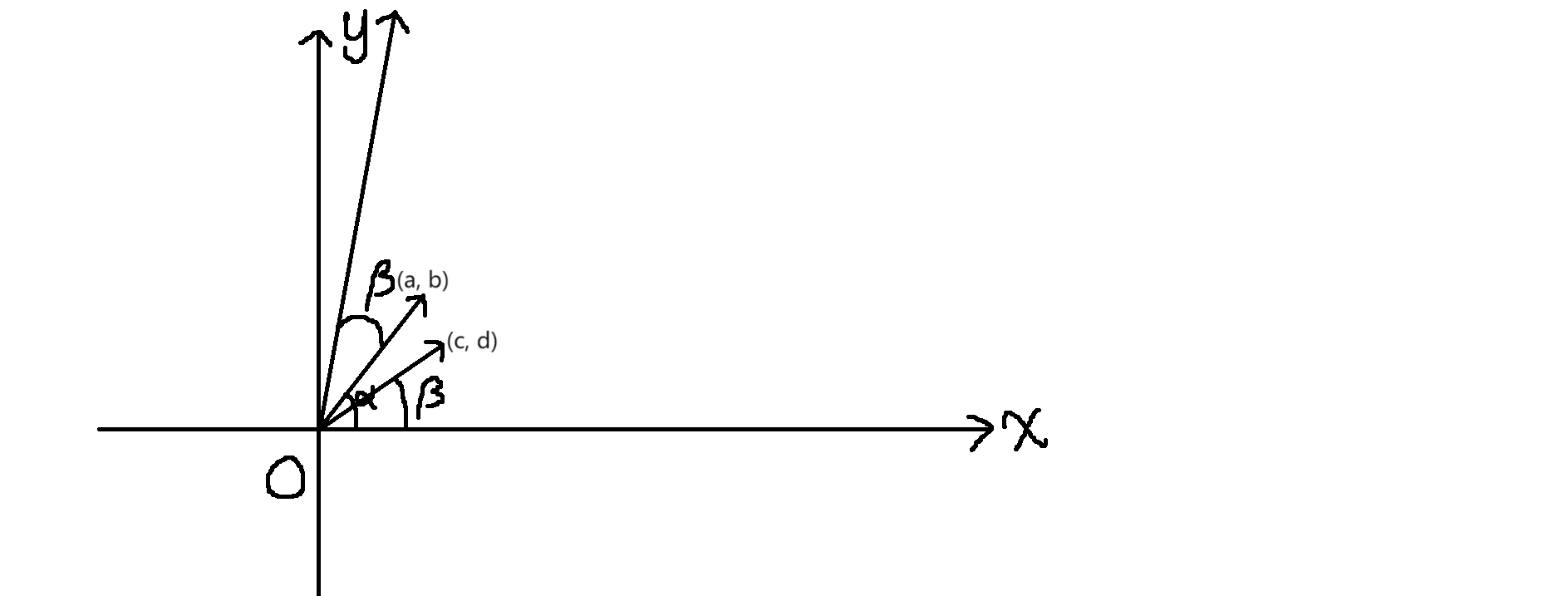
前置知识：单位根

声明：以下为了方便书写，均将 $\omega_n^i$ 表示为 $\omega_i$。

代数基本定理：任何复系数一元 $n$ 次多项式方程在复数域上至少有一根。~~（我也不会证qwq）~~

推论：任何复系数一元$n$次多项式方程在复数域上恰好$n$个根。

证：若一个方程有一根$x_1$，则此方程可以写成$(x - x_1) \times $(原方程降幂一次的多项式)，最多可以降幂$n$次，因此恰好有$n$个根。

单位根：$x^n - 1 = 0$的$n$个根，记作$\omega_1, \omega_2, \omega_3 \dots \dots \omega_n$

求解单位根：在坐标轴中画出单位圆(以$(0, 0)$为圆心，$1$为半径的圆)，如图：

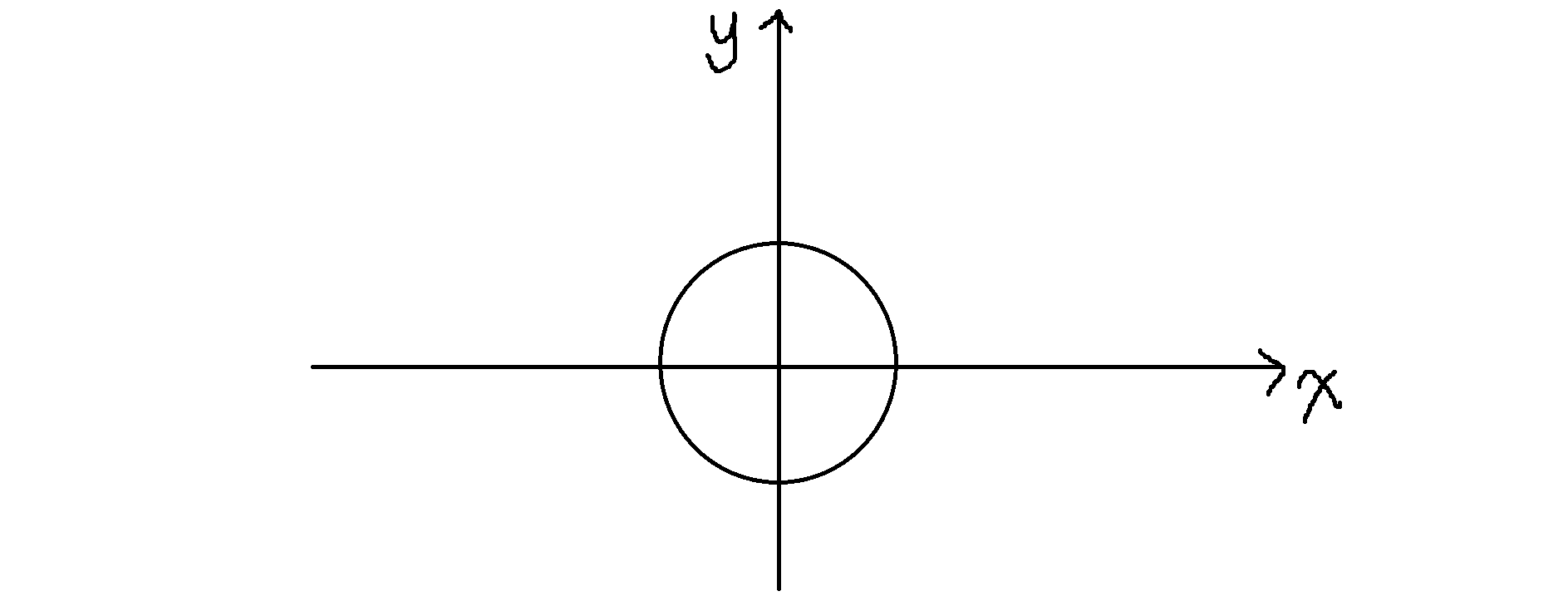
将$x$当做向量$\overrightarrow{x}$，则根据向量乘法，$\overrightarrow{x}$的模长应为$1$，由于有$n$个根，所以要将这个圆分成$n$分，为方便计算，规定$\overrightarrow{x_1}$为从$(0, 0)$指向$(1, 0)$的向量，就得到了这$n$个单位根。以$n = 6$时为例子，如图：

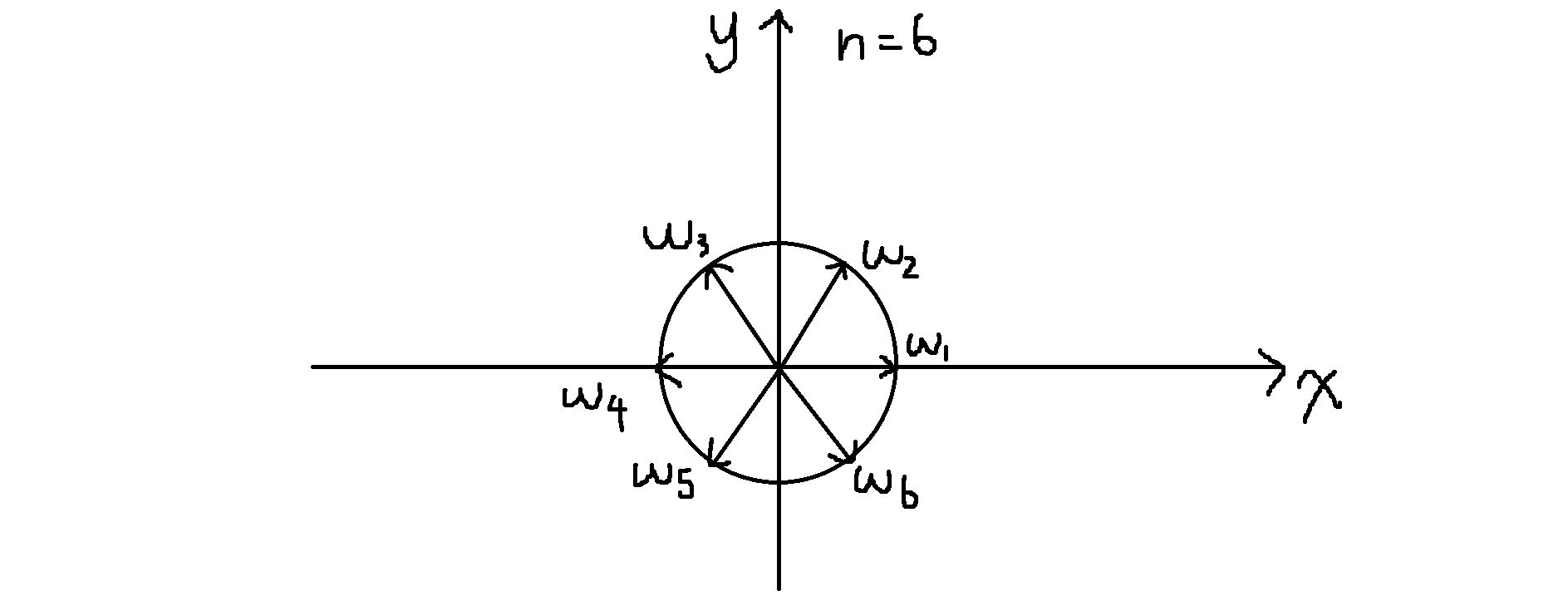
由三角函数和复数与向量的关系可得：$w_i=\cos{\displaystyle\frac{2i\pi}n}+i\sin{\displaystyle\frac{2i\pi}n}$

如果我们按照这个等式拓宽 $w_i$ 中 $i$ 的范围的话，结合其几何意义，我们可以得到 $w_i$ 一些~~有趣的~~性质：

1、$w_{i+n}=w_i$(相当于绕着原点转了$1$圈)
2、$w_iw_j=w_{i+j}$(相当于先顺时针走了$i$个单位根，又顺时针走了$j$个单位根)
3、$w_{i}^j=w_{ij}$(从二性质拓展得来)
4、$-w_i=w_{-i}$(顺时针走$i$个在取反，等于逆时针走$i$个)
5、$w_{ki}$=$w'_{i}$，其中 $w_i$ 是 $kn$ 次单位根，$w'_i$ 是 $n$ 次单位根。(相当于保持这$n$个单位根不变，在每两个单位根之间加入$(k - 1)$个单位根)

正题：DFT

终于切入正题了，~~前方高能~~

根据多项式插值中提到的原理我们可以联想到这样一个解决多项式相乘的算法：

将 $F(x)$ 和 $G(x)$ 进行多点求值，得到 $(x_1,F(x_1)),(x_2,F(x_2))\dots(x_n,F(x_n))$ 和 $(x_1,G(x_1)),(x_2,G(x_2))\dots(x_n,G(x_n))$ 这两系列点。

我们可以知道的是：$H(x)=F(x)G(x)$，所以就有 $\forall_{i}H(x_i)=F(x_i)G(x_i)$。

所以我们直接将两系列点对应相乘，得到的一系列点就是 $H(x)$ 上的点。利用这些点进行插值即可得到 $H(x)$ 的表达式。

那么如何适当的选取 $x_1,x_2\dots x_n$，使得多点求值能够快速进行？

我们可以取 $x_i=w_i$($w_i$是$n$次单位根的第$i$个)(因为单位根满足如上的性质)

定义操作$DFT:\{f_i\}\rightarrow\{F(w_i)\}$，即输入一个$n-1$次多项式的系数列，得到其在$n$次单位根处的点值列。

现在复杂度还是$O(n^2)$，需要优化。

当我们想求 $DFT(F)$ 时，也就是要求 $F(\omega_k) = \displaystyle\sum_{i=0}^{n - 1}{f_i\omega_k^i}$

按照奇偶次幂分组，用$x$替换$\omega_k$：原式 $= (f_0 + f_2x^2 + f_4x^4 + \dots + f_{n - 2}x^{n - 2}) + (f_1x + f_3x^3 + f_5x^5 + \dots + f_{n - 1}x^{n - 1}) = \displaystyle\sum_{i=0}^{\frac n2-1}{f_{2i}x^{2i}} + \displaystyle\sum_{i=0}^{\frac n2-1}{f_{2i+1}x^{2i+1}} = \displaystyle\sum_{i=0}^{\frac n2-1}{f_{2i}x^i} + x\displaystyle\sum_{i=0}^{\frac n2-1}{f_{2i + 1}x^{i}}$($x$是变量)

设$F_1(x) = \displaystyle\sum_{i=0}^{\frac n2-1}{f_{2i}x^i}$。

$F_2(x) = \displaystyle\sum_{i=0}^{\frac n2-1}{f_{2i + 1}x^{i}}$

那么可以知道$F(x) = F_1(x) + xF_2(x)$

将$\omega_k(k ＜ \frac n2)$代入式子中，得到$F(w_k) = F_1(\omega_k') + \omega_kF_2(\omega_k')$($\omega'$表示$n \rightarrow \frac n2$时的单位根)

将$\omega_{k + \frac n2}(k ＜ \frac n2)$代入式子中，得到$F(w_{k + \frac n2}) = F_1(\omega_{2k}) - \omega_kF_2(\omega_{2k})$

观察上下两个式子，这两个式子只有一个常数项不同。

那么当我们在枚举第一个式子的时候，我们可以$O(1)$的得到第二个式子的值。

容易发现复杂度满足$T(n)=2T(\frac n2)+O(n)$，根据主定理可知复杂度为 $O(n\log{n})$。

于是我们在$O(n\log n)$的时间复杂度内求得了 $DFT(F)$。

代码：(仅展示$DFT$)

void DFT(complex <double> *f, int n){
	if(n == 1)
		return;
	for(int i = 0; i < n; i++)//因为是(n - 1)次多项式
		tmp[i] = f[i];
	for(int i = 0; i < n; i++){
		if(i % 2 == 1)
			f[n / 2 + i / 2] = tmp[i];//奇数项放左边
		else
			f[i / 2] = tmp[i];//偶数项放右边
	}
	complex <double> *f1 = f;
	complex <double> *f2 = f + n / 2;
	DFT(f1, n / 2);//递归左边
	DFT(f2, n / 2);//递归右边
	complex <double> cur(1, 0), step(cos(2 * M_PI / n), sin(2 * M_PI / n));//cur记录当前单位根，cur*step让cur成为下一个单位根
	for(int k = 0; k < n / 2; k++){
		tmp[k] = f1[k] + cur * f2[k];//第一个公式
		tmp[k + n / 2] = f1[k] - cur * f2[k];//第二个公式
		cur *= step;//cur变成下一个单位根
	}
	for(int i = 0; i < n; i++)
		f[i] = tmp[i];
}

中置知识：单位根反演

$\displaystyle\sum_{i=0}^{n - 1}\omega_i^k = n[n \mid k]$

证：原式 $= \displaystyle\sum_{i=0}^{n - 1}\omega_{ik}$(单位根性质3) $= \displaystyle\sum_{i=0}^{n - 1}\omega_k^i$(单位根性质3反操作)

现在等式变成了一个等比数列

小知识：等比数列求和

$q + qp + qp^2 + \dots + qp^n = x$

解：当$p = 1$时，相当于$n$个$q$相加，$x = nq$；

当$p \neq 1$时，$\because x = q + qp + qp^2 + \dots + qp^n$①

$\therefore px = qp + qp^2 + qp^3 + \dots + qp^{n + 1}$②

① - ②得：$(1 - p)x = q - qp^{n +1}$

$x = \displaystyle\frac{q - qp^{n + 1}}{1 - p}$

$\therefore$ 原式 $= \displaystyle\frac{1 - \omega_k^n}{1 - w_k}$

当$n \mid k$时，有公比 $w_k = 1$，所以 $\displaystyle\sum_{i=0}^{n - 1}{\omega_k^i} = n$

当$n\nmid k$，有公比 $w_k \neq 1$，所以 $\displaystyle\sum_{i=0}^{n - 1}{\omega_k^i} = 0$

证明完毕。

开始反演：$nf_k = \displaystyle\sum_{i=0}^{n - 1}w_{-k}^iF(\omega_i)$

$F(w_k) = \displaystyle\sum_{i=0}^{n - 1}\omega_k^if_i$

证：$nf_k = \displaystyle\sum_{i=0}^{n - 1}\omega_{-k}^i\displaystyle\sum_{j=0}^{n - 1}\omega_k^jf_j$(将第二个式子代入第一个式子) $= \displaystyle\sum_{i=0}^{n - 1}\displaystyle\sum_{j=0}^{n - 1}\omega_{-k}^i\omega_k^jf_j$(将求和移动到最外层) $= \displaystyle\sum_{i=0}^{n - 1}\displaystyle\sum_{j=0}^{n - 1}\omega_{-ik}\omega_{kj}f_j$(单位根性质3) $= \displaystyle\sum_{i=0}^{n - 1}\displaystyle\sum_{j=0}^{n - 1}\omega_{i(j - k)}f_j$(单位根性质2) $= \displaystyle\sum_{i=0}^{n - 1}\displaystyle\sum_{j=0}^{n - 1}\omega_i^{j - k}f_j$(单位根性质3反操作) $= \displaystyle\sum_{j=0}^{n - 1}f_j\displaystyle\sum_{i=0}^{n - 1}\omega_i^{j - k}$(交换求和顺序) $= \displaystyle\sum_{j=0}^{n - 1}f_jn[n \mid (j - k)]$(第一个公式) $= \displaystyle\sum_{j=0}^{n - 1}f_jn[j = k]$($j \leq n - 1, k \leq n - 1$，因此$k - j \leq n$，只有当$k - j = 0$时，$(j - k) \div n$才$=$整数，即$j = k$) = nf_k

证明完毕

正题：IDFT

定义操作$IDFT:\{H(w_i)\}\rightarrow\{h_i\}$，即输入一个多项式在$n$次单位根处的点值列，得到其$n-1$次的系数列。

当我们想求 $IDFT(h)$ 时，也就是要求 $nh_k = \displaystyle\sum_{i=0}^{n - 1}{H(\omega_i)\omega_{-k} ^i}$

有了这个式子之后，我们惊奇的发现$IDFT$的操作几乎和$DFT$一样，因此同样可以做到$O(n\log n)$的复杂度。

代码：(和$DFT$很像)

void IDFT(complex <double> *H, int n){
	if(n == 1)
		return;
	for(int i = 0; i < n; i++)
		tmp[i] = H[i];
	for(int i = 0; i < n; i++){
		if(i % 2 == 1)
			H[n / 2 + i / 2] = tmp[i];
		else
			H[i / 2] = tmp[i];
	}
	complex <double> *H1 = H;
	complex <double> *H2 = H + n / 2;
	IDFT(H1, n / 2);
	IDFT(H2, n / 2);
	complex <double> cur(1, 0), step(cos(2 * M_PI / n), sin(2 * M_PI * (-1)/*唯一区别*/ / n));
	for(int k = 0; k < n; k++){
		tmp[k] = H1[k] + cur * H2[k];
		tmp[k + n / 2] = H1[k] - cur * H2[k];
		cur *= step;
	}
	for(int i = 0; i < n / 2; i++)
		H[i] = tmp[i];
}

完整代码：P3803 【模板】多项式乘法（FFT）

#include <bits/stdc++.h>
using namespace std;
const int N = 5e6 + 9;
complex <double> tmp[N << 1];
void DFT(complex <double> *f, int n){
	if(n == 1)
		return;
	for(int i = 0; i < n; i++)
		tmp[i] = f[i];
	for(int i = 0; i < n; i++){
		if(i % 2 == 1)
			f[n / 2 + i / 2] = tmp[i];
		else
			f[i / 2] = tmp[i];
	}
	complex <double> *f1 = f;
	complex <double> *f2 = f + n / 2;
	DFT(f1, n / 2);
	complex <double> cur(1, 0), step(cos(2 * M_PI / n), sin(2 * M_PI / n));
	for(int k = 0; k < n / 2; k++){
		tmp[k] = f1[k] + cur * f2[k];
		tmp[k + n / 2] = f1[k] - cur * f2[k];
		cur *= step;
	}
	for (int i = 0; i < n; i++)
		f[i] = tmp[i];
}
void IDFT(complex <double> *f, int n){
	if(n == 1)
		return;
	for(int i = 0; i < n; i++)
		tmp[i] = f[i];
	for(int i = 0; i < n; i++){
		if(i % 2 == 1)
			f[n / 2 + i / 2] = tmp[i];
		else
			f[i / 2] = tmp[i];
	}
	complex <double> *f1 = f;
	complex <double> *f2 = f + n / 2;
	IDFT(f1, n / 2);
	IDFT(f2, n / 2);
	complex <double> cur(1, 0), step(cos(2 * M_PI / n), sin(2 * M_PI * (-1) / n));
	for(int k = 0; k < n / 2; k++){
		tmp[k] = f1[k] + cur * f2[k];
		tmp[k + n / 2] = f1[k] - cur * f2[k];
		cur *= step;
	}
	for(int i = 0; i < n; i++)
		f[i] = tmp[i];
}
int n, m;
complex <double> f[N << 1], g[N << 1];
int main(){
	scanf("%d%d", &n, &m);
	for(int i = 0; i <= n; i++){
		double tmp;
		scanf("%lf", &tmp);
		complex <double> tmpp(tmp, 0);
		f[i] = tmpp;
	}
	for(int i = 0; i <= m; i++){
		double tmp;
		scanf("%lf", &tmp);
		complex <double> tmpp(tmp, 0);
		g[i] = tmpp;
	}
	int lim = 1;
	while(lim <= n + m)
		lim <<= 1;
	DFT(f, lim);
	DFT(g, lim);
	for(int i = 0; i <= lim; i++)
		f[i] *= g[i];
	IDFT(f, lim);
	for(int i = 0; i <= n + m; i++)
		printf("%d ", int(f[i].real() / lim + 0.5));
	return 0;
}

正题：非递归IDFT

观察IDFT递归顺序，如图：

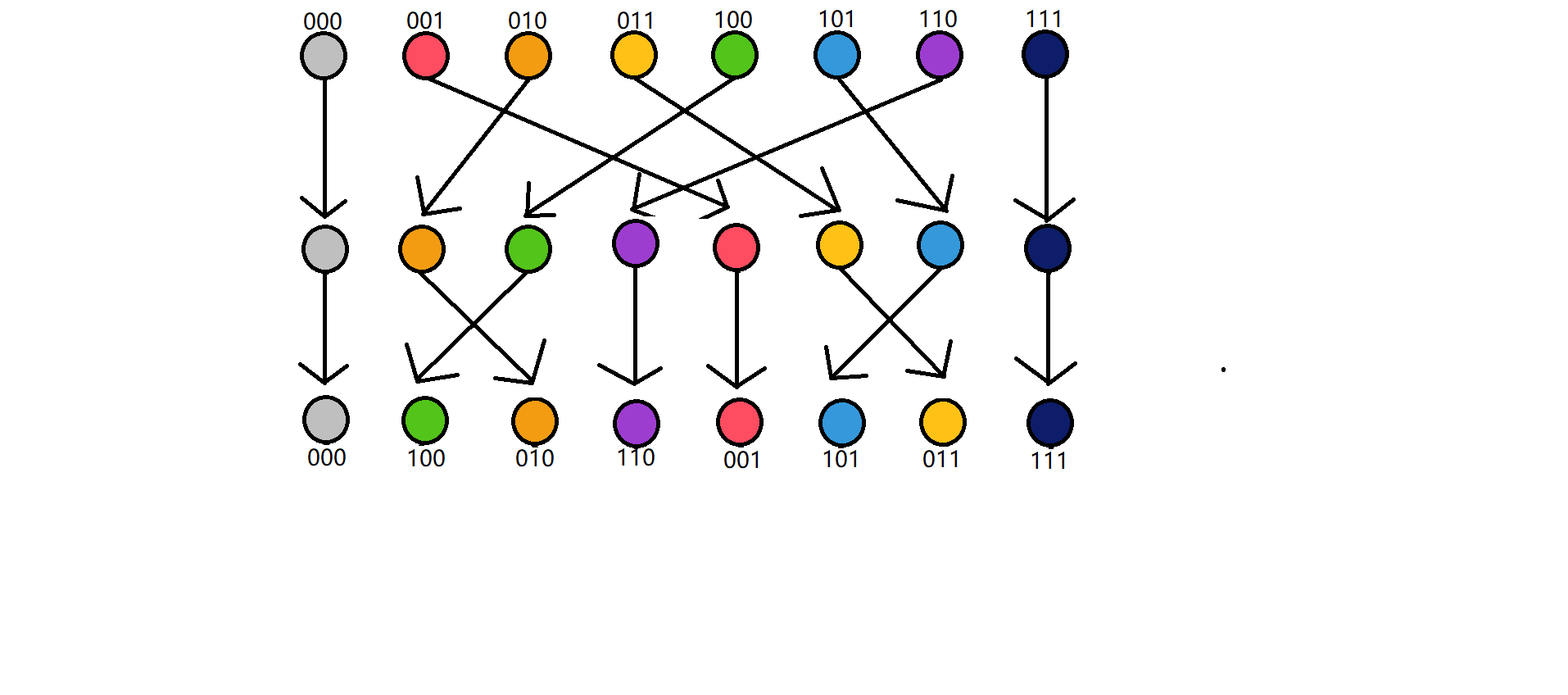
~~颜色非常有寓意~~

最后序列的顺序，等于将原序列下标二进制拆分，前后反转，从新排序。

因此我们可以非递归地完成这一步操作，然后再非递归地往上合并，可以缩减递归所需的花销。

在注意到交换位置的过程实际上可以通过一定的预处理做到$O(n)$，可以进一步提升效率。

完整代码：P3803 【模板】多项式乘法（FFT）

#include <bits/stdc++.h>
using namespace std;
const int N = 5e6 + 9;
int rev[N];
void DFT(complex <double> *f, int n){
	//找到第一层该数字在什么位置 
	for(int i = 0; i < n; i++){
		rev[i] = rev[i >> 1] >> 1;
		if(i % 2 == 1)
			rev[i] |= n >> 1;
	}
	for(int i = 0; i < n; i++)
		if(i < rev[i])
			swap(f[i], f[rev[i]]);
	for(int h = 2; h <= n; h <<= 1){//每上升一层，每一块数大小加倍 
		complex <double> step(cos(2 * M_PI / h), sin(2 * M_PI / h));
		for(int j = 0; j < n; j += h){//枚举每一块数 
			complex <double> cur(1, 0);
			for(int k = j; k < j + h / 2; k++){//计算H(\omega_k)
				complex <double> c1 = f[k], c2 = cur * f[k + h / 2]; 
				f[k] = c1 + c2;//根据图理解
				f[k + h / 2] =  c1 - c2;
				cur *= step;
			} 
		}
	}
}
void IDFT(complex <double> *f, int n){
	for(int i = 0; i < n; i++){
		rev[i] = rev[i >> 1] >> 1;
		if(i % 2 == 1)
			rev[i] |= n >> 1;
	}
	for(int i = 0; i < n; i++)
		if(i < rev[i])
			swap(f[i], f[rev[i]]);
	for(int h = 2; h <= n; h <<= 1){
		complex <double> step(cos(2 * M_PI / h), sin(2 * M_PI * (-1)/*注意*/ / h));
		for(int j = 0; j < n; j += h){
			complex <double> cur(1, 0);
			for(int k = j; k < j + h / 2; k++){ 
				complex <double> c1 = f[k], c2 = cur * f[k + h / 2]; 
				f[k] = c1 + c2;
				f[k + h / 2] =  c1 - c2;
				cur *= step;
			} 
		}
	}
}
int n, m;
complex <double> f[N << 1], g[N << 1];
int main(){
	scanf("%d%d", &n, &m);
	for(int i = 0; i <= n; i++){
		double tmp;
		scanf("%lf", &tmp);
		complex <double> tmpp(tmp, 0);
		f[i] = tmpp;
	}
	for(int i = 0; i <= m; i++){
		double tmp;
		scanf("%lf", &tmp);
		complex <double> tmpp(tmp, 0);
		g[i] = tmpp;
	}
	int lim = 1;
	while(lim <= n + m)
		lim <<= 1;
	DFT(f, lim);
	DFT(g, lim);
	for(int i = 0; i <= lim; i++)
		f[i] *= g[i];
	IDFT(f, lim); 
	for(int i = 0; i <= n + m; i++)
		printf("%d ", int(f[i].real() / lim + 0.5));
	return 0;
}

快速数论变换NTT

前置知识：原根

若$a^{\varphi(p)} \equiv 1 (\text{mod } m)$, 且对$\forall x \in [0, \varphi(p) - 1], a^x \not\equiv 1 (\text{mod } m)$，则称$a$为$p$的原根。

有趣的知识：$998244353$的一个原根是$114514$(°O °)

正题

设$g$表示$p$的一个原根，则令 $\omega_i=g^{i\frac{\varphi(p)}n}$ 就具有同复数域中单位根一样的性质。(见快速傅里叶变换FFT/前置知识：单位根/单位根的性质)

但是这不代表我们可以直接将他套用进 FFT 中。因为这里必须要求 $n\mid \varphi(p)$，所以这对 $n$ 产生了很大的限制。

幸运的是我们发现质数 $998244353$ 的欧拉函数值 $998244352=119\times2^{23}$，因此当$n \leq 2^{23}$ 时，都能够很好的进行这个算法，这也是$998244353$成为常用模数的原因。(尽管有些时候题目与多项式无关)

完整代码：P3803 【模板】多项式乘法（FFT）

#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 5e6 + 9, MOD = 998244353;
int rev[N];
int qpow(int x, int y){
	int res = 1;
	while(y){
		if(y & 1)
			res = res * x % MOD;
		x = x * x % MOD;
		y >>= 1;
	}
	return res;
}
void NTT(int *f, int n, int opt){
	for(int i = 0; i < n; i++){
		rev[i] = rev[i >> 1] >> 1;
		if(i % 2 == 1)
			rev[i] |= n >> 1;
	}
	for(int i = 0; i < n; i++)
		if(i < rev[i])
			swap(f[i], f[rev[i]]);
	for(int h = 2; h <= n; h <<= 1){
		int mi = h >> 1;
		int gn = qpow(3, (MOD - 1) / h);
		for(int j = 0; j < n; j += h){
			int g = 1;
			for(int k = 0; k < mi; k++){
				int tmp = f[j + k + mi] * g % MOD;
				f[j + k + mi] = (f[j + k] - tmp + MOD) % MOD;
				f[j + k] = (f[j + k] + tmp) % MOD;
				g = g * gn % MOD;
			}
		}
	}
	if(opt == -1){
		reverse(f + 1, f + n);
	    int inv = qpow(n, MOD - 2);
	    for(int i = 0; i < n; i++)
			f[i] = f[i] * inv % MOD;
	}
}
int f[N << 1], g[N << 1], n, m;
signed main(){
	scanf("%lld%lld", &n, &m);
	for(int i = 0; i <= n; i++)
		scanf("%lld", &f[i]);
	for(int i = 0; i <= m; i++)
		scanf("%lld", &g[i]);
	int lim = 1;
	while(lim <= n + m)
		lim <<= 1;
	NTT(f, lim, 1);
	NTT(g, lim, 1);
	for(int i = 0; i <= lim; i++)
		f[i] = f[i] * g[i] % MOD;
	NTT(f, lim, -1); 
	for(int i = 0; i <= n + m; i++)
		printf("%lld ", f[i]);
	return 0;
}

posted @ 2024-08-01 16:37 JPGOJCZX 阅读(1) 评论(0) 编辑收藏举报

刷新页面返回顶部

JPGOJCZX

多项式学习笔记（一）（2024.7.6）

暴力多项式计算

加法

乘法

求逆

除法/取模

求导/积分

前置知识：求导及其特性

前置知识：不定积分及其特性

正题

开根

对数函数

指数函数

三角函数

前置知识：泰勒级数与泰勒展开

正题

快速傅里叶变换FFT

前置知识：多项式插值

前置知识：复数运算

前置知识：向量运算

前置知识：单位根

正题：DFT

中置知识：单位根反演

正题：IDFT

正题：非递归IDFT

快速数论变换NTT

前置知识：原根

正题

公告